VnDoc.com

Diện tích mặt cầu và thể tích của hình cầu

Chuyên đề Toán lớp 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề thi vào lớp 10: Diện tích và thể tích của hình cầu

1. Hình cầu
2. Công thức diện tích mặt cầu
3. Thể tích của hình cầu
4. Bài tập ví dụ cho các bài toán về hình cầu
5. Bài tập tự luyện các bài toán về hình cầu

Diện tích mặt cầu và thể tích hình cầu là một dạng toán mới, được đưa vào trong các đề thi tuyển sinh vào lớp 10 môn Toán gần đây. Tài liệu được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

Tài liệu dưới đây được VnDoc biên soạn gồm hướng dẫn giải chi tiết cho dạng bài liên quan đến tính diện tích mặt cầu và thể tích hình cầu và tổng hợp các bài toán để các bạn học sinh có thể luyện tập thêm. Qua đó sẽ giúp các bạn học sinh ôn tập các kiến thức, chuẩn bị cho các bài thi học kì và ôn thi vào lớp 10 hiệu quả nhất. Sau đây mời các bạn học sinh cùng tham khảo tải về bản đầy đủ chi tiết.

1. Hình cầu

Hình vẽ minh họa:

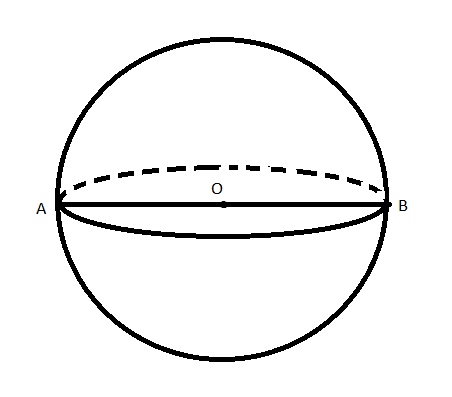
Diện tích mặt cầu và thể tích của hình cầu

Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu

+ Điểm O được gọi là tâm, độ dài R là bán kính của hình cầu

+ Nửa đường tròn trong phép quay tạo nên mặt cầu

2. Công thức diện tích mặt cầu

Công thức tính diện tích mặt cầu

Diện tích của một mặt cầu được xác định bởi công thức sau:

$S = 4\pi {R^2} = \pi {d^2}$

Trong đó R là bán kính của đường tròn và d là đường kính của mặt cầu

3. Thể tích của hình cầu

Công thức tính thể tích hình cầu

Thể tích của hình cầu bán kính R là: $V = \frac{4}{3}\pi {R^3}$

4. Bài tập ví dụ cho các bài toán về hình cầu

Bài 1: Tính diện tích của mặt cầu có thể tích bằng $36\pi$ cm³

Hướng dẫn giải

Bán kính của đường tròn là: $V = \frac{4}{3}\pi {R^3} = 36\pi \Leftrightarrow {R^3} = 27 \Leftrightarrow R = 3$ cm

Diện tích cảu mặt cầu là: $S = 4\pi {R^2} = 4\pi .9 = 36\pi$ cm²

Bài 2: Tính diện tích xung quanh của hình nón có chu vi đáy là $24\pi$ cm và độ dài 1 đường sinh là 15cm

Hướng dẫn giải

Bán kính đáy là: $2\pi r = 24\pi \Leftrightarrow r = 12$ cm

Diện tích xung quanh của hình nón là: ${S_{xq}} = \pi rl = \pi .24.15 = 360\pi$ cm²

Bài 3: Người ta làm các viên nước đá hình cầu có bán kính là 2cm. Cho 6 viên nước đá như vậy vào một cốc thủy tinh hình trụ rồi rót nước giải khát vào cho đầy cốc. Biết rằng cột nước hình trụ ở cốc có bán kính đáy là 3cm, chiều cao cột nước là 12cm. Tính thể tích nước giải khát rót vào cốc.

Hướng dẫn giải

Thể tích của một viên nước đá hình cầu là: $\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .8 = \frac{{32}}{3}\pi$ cm³

Thể tích của 6 viên nước đá hình cầu là: $6.\frac{{32}}{3}\pi = 64\pi$ cm³

Thể tích của cốc thủy tinh hình trụ là: $\pi {r^2}h = \pi .9.12 = 36\pi$ cm³

Thể tích nước giải khát rót vào cốc là: $64\pi - 36\pi = 28\pi$ cm³.

Bài 4. Một tháp nước có bể chứa là một hình cầu, đường kính bên trong của bể đo được là 6 mét. Người ta dự tính lượng nước đựng đầy trong bể đủ dùng cho một khu dân cư trong 5 ngày. Cho biết khu dân cư đó có người. Hỏi người ta đã dự tính mức bình quân mỗi người dùng bao nhiêu lít nước trong một ngày? (Lấy $\pi \approx 3,14$ , kết quả làm tròn đến chữ số thập phân thứ nhất)

Hướng dẫn giải

Bán kính hình cầu cuả bể nước là:

Thể tích của bể nước hình cầu là: $V = \frac{4}{3}\pi R^{3} = \frac{4}{3}.3,14.3^{3} = 113,04\left( m^{3} \right) = 113040$ (lít)

Lượng nước chứa đầy bể xấp xỉ 113040 lít nước

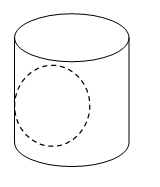
Bài 5. Một bình hình trụ có đường kính đáy 1dm, chiều cao 2dm bên trong có chứa viên bi hình cầu có bán kính 4cm. Hỏi phải đổ vào bình bao nhiêu lít nước để nước đầy bình (làm tròn đến chữ số thập phân thứ nhất).

Cho biết: $V_{Tru} = \pi.r^{2}h$ với là bán kính đáy; là chiều cao hình trụ. $V_{CÇu} = \frac{4}{3}\pi R^{3}$ với là bán kính hình cầu

Hướng dẫn giải

Đổi đơn vị: 4 cm = 0,4 dm.

Thể tích của viên bi là: $V_{C} = \frac{4}{3}\pi R^{3} = \frac{4}{3}\pi.(0,4)^{3} = \frac{32}{375}\pi$ (dm³)

Hình trụ có bán kính đáy bằng dm và có chiều cao dm.

Thể tích của hình trụ là $V_{T} = \pi.r^{2}h = \pi.(0.5)^{2}.2 = \frac{\pi}{2}$ (dm³).

Số nước cần phải đổ để nước đầy bình là: $\frac{\pi}{2} - \frac{32\pi}{375} = \frac{311\pi}{750} \approx 1,3$ (dm³)

Vậy số nước cần phải đổ để nước đầy bình là: 1,3 lít.

Bài 6. Cho nửa đường tròn tâm , đường kính , và là hai tiếp tuyến với nửa mặt đường tròn tại và . Lấy trên điểm rồi vẽ tiếp tuyến cắt tại .

a) Chứng minh $\bigtriangleup MON \backsim \bigtriangleup APB$ .

b) Chứng minh $AM \cdot BN = R^{2}$ .

c) Tính tỉ số $\frac{S_{MON}}{S_{APB}}$ khi $AM = \frac{R}{2}$ .

d) Tính thể tích của hình do nửa hình tròn quay quanh sinh ra.

Hướng dẫn giải

Hình vẽ minh họa

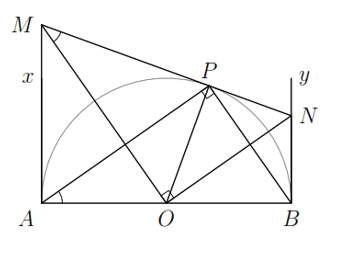
a) Ta có:

- Góc $\widehat{APB} = 90^{{^\circ}}$ (góc nội tiếp chắn nửa đường tròn).

- Theo tính chất của hai tiếp tuyến cắt nhau ta có:

là tia phân giác của $\widehat{AOP}$ và là tia phân giác của góc $\widehat{BOP}$ .

Mà $\widehat{AOP}$ và $\widehat{BOP}$ là 2 góc kề bù $\Rightarrow$ $OM\bot ON$

$\Rightarrow$ $\widehat{MON} = 90^{{^\circ}}$ .

- Xét tứ giác có $\widehat{MPO} = \widehat{MAO} = 90^{{^\circ}}$ .

$\widehat{OMP}$ và $\widehat{PAO}$ cùng chắn cung $OP \Rightarrow$ $\widehat{OMP} = \widehat{PAO}$ .

$\left\{ \begin{matrix} \widehat{MON} = \widehat{APB} = 90^{{^\circ}} \\ \widehat{BAP} = \widehat{OMN} \\ \end{matrix} \right.$ .

$\Rightarrow \bigtriangleup MON \backsim \bigtriangleup APB$ (g.g).

b) $AM \cdot BN = MP \cdot NP = OP^{2} = R^{2}$ .

c) $AM \cdot BN = R^{2} \Rightarrow BN = 2R$ .

$\Rightarrow MN = \frac{5R}{2}$ $\Rightarrow \frac{S_{MON}}{S_{APB}} = \left( \frac{MN}{AB} \right)^{2} = \frac{25}{16}$ .

d) Nửa hình tròn quay quanh là hình cầu đường kính $\Rightarrow$ $V = \frac{4}{3}\pi R^{3}$ .

5. Bài tập tự luyện các bài toán về hình cầu

Bài tập 1. Một hình nón có bán kính đáy bằng cm và có diện tích xung quanh bằng diện tích của mặt cầu có bán kính cm. Tính chiều cao của hình nón.

Bài tập 2. Một cái hộp hình trụ được làm ra sao cho một quả bóng hình cầu đặt vừa khít vào hộp đó như hình vẽ.

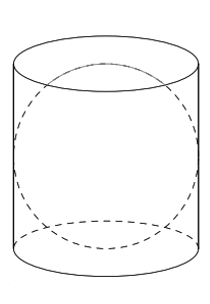
Tính tỉ số thể tích của hình cầu và hình trụ?

Bài tập 3. Chiều cao của một hình trụ gấp 3 lần bán kính đáy của nó. Tỉ số của thể tích hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ bằng bao nhiêu?

Bài tập 4. Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính cm như hình vẽ.

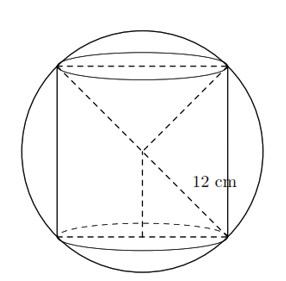
Tính:

a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.

Đáp án: … $\left( cm^{2} \right)$

b) Thể tích của hình cầu.

Đáp án: … $\left( cm^{3} \right)$

c) Diện tích mặt cầu.

Đáp án: … $\left( cm^{2} \right)$

Bài tập 5. Cho tam giác đều có cạnh cm, đường cao . Khi đó diện tích mặt cầu được tạo thành khi quay nửa đường tròn nội tiếp $\bigtriangleup ABC$ một vòng quanh .

Bài tập 6. Cho tam giác vuông cân tại có cạnh góc vuông bằng . Tính diện tích mặt cầu được tạo thành khi quay nửa đường tròn ngoại tiếp tam giác một vòng quanh cạnh .

Bài tập 7. Cho tam giác đều có cạnh $AB = 8\text{ }cm$ , đường cao . Khi đó thể tích hình cầu được tạo thành khi quay nửa đường tròn nội tiếp tam giác một vòng quanh .

Bài tập 8. Cho hình chữ nhật có $AB = 4\text{ }cm;AD = 3\text{ }cm$ . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật quay quanh đường thẳng với là trung điểm là trung điểm .

Bài tập 9. Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa diện tích mặt cầu và diện tích toàn phần của hình lập phương.

Đáp án bài tập tự rèn luyện

Bài tập 1.

Áp dụng công thức tính diện tích xung quanh hình nón $S_{xq} = \pi rl = 3\pi l$ .

Áp dụng công thức tính diện tích mặt cầu $S_{c} = 4\pi R^{2} = 36\pi$ .

Từ giả thuyết $S_{xq} = S_{c}$ ta được $3\pi l = 36\pi$

$\Rightarrow l = 12 \Rightarrow h = \sqrt{12^{2} - 3^{2}} = 3\sqrt{15}$ cm.

Bài tập 2.

Nhận thấy $R_{c} = R_{t} = r$ và . Nên $V_{c} = \frac{4}{3}\pi r^{3}$ và

$V_{t} = \pi r^{2}h = 2\pi r^{3} \Rightarrow \frac{V_{c}}{V_{t}} = \frac{2}{3}$ .

📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.

--------------------------------------------------------------

Ngoài các dạng Toán 9 ôn thi vào lớp 10 trên, mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt!

Tải về

Chọn file muốn tải về: