VnDoc.com

Chuyên đề Phương trình bậc hai chứa tham số Toán 9 (Có đáp án)

Tài liệu đại số Toán 9 ôn thi vào 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Loại File: PDF

Phân loại: Tài liệu Tính phí

Chuyên đề Phương trình bậc hai chứa tham số Toán 9

(Có đáp án)

Chuyên đề Phương trình bậc hai chứa tham số là dạng bài thường gặp trong chương trình Toán lớp 9 cũng như thi vào lớp 10. Để giúp các em học sinh nắm vững phần này, VnDoc gửi tới các bạn Chuyên đề Phương trình bậc hai chứa tham số. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hơn.

Tài liệu Phương trình bậc hai chứa tham số được chia làm hai phần: Lý thuyết và bài tập vận dụng. Phần lý thuyết có các bài tập ví dụ để các bạn học sinh tham khảo. Phần bài tập được sưu tầm và chọn lọc để các bạn học sinh có thể áp dụng lý thuyết phía trên vận dụng làm bài. Qua đó sẽ giúp cho các bạn học sinh ôn tập và củng cố lại kiến thức về Phương trình bậc hai chứa tham số đồng thời nắm vững các kiến thức để chuẩn bị cho kì thi tuyển sinh vào lớp 10.

A. Công thức giải bài toán phương trình bậc hai chứa tham số

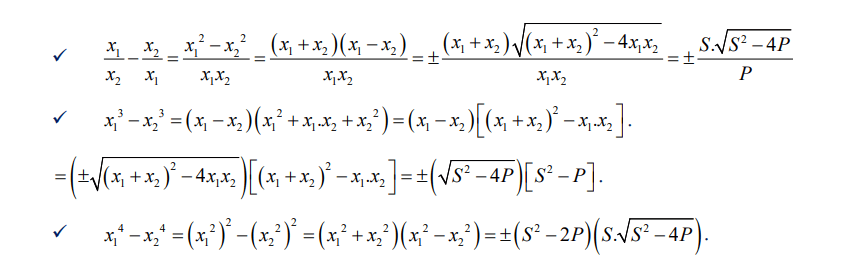
B. Các dạng bài tập về phương trình bậc hai chứa tham số có hướng dẫn

Câu 1: Cho phương trình $x^{2} - 2m + 1x + m^{2} + m - 1 = 0$ ( là tham số).

a) Chứng minh rằng phương trình luôn có nghiệm vói mọi .

b) Gọi $x_{1},x_{2}$ là hai nghiệm của phương trình. Tìm sao cho $A = \left( 2x_{1} - x_{2} \right)\left( 2x_{2} - x_{1} \right)$ đạt giá trị nhỏ nhất và tính giá trị nhỏ nhất đó.

Hướng dẫn giải

Xét $2m - 1 = 0 \Rightarrow m = \frac{1}{2}$ phương trình trở thành $- x + 1 = 0 \Rightarrow x = 1 \notin ( - 1;0)$

Xét $2m - 1 \neq 0 \Rightarrow m \neq \frac{1}{2}$ khi đó ta có:

$\Delta' = m^{2} - (2m - 1) = m^{2} -2m + 1 = (m - 1)^{2} \geq 0$ với mọi m

Suy ra phương trình có nghiệm với mọi .

Ta thấy nghiệm không thuộc khoảng

Với $m \neq \frac{1}{2}$ phương trình còn có nghiệm là $x = \frac{m - m + 1}{2m - 1} = \frac{1}{2m - 1}$

Phương trình có nghiệm trong khoáng suy ra

$- 1 \leq \frac{1}{2m - 1} \leq 0\Leftrightarrow \left\{ \begin{matrix}\dfrac{1}{2m - 1} + 1 > 0 \\2m - 1 < 0\end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix}\dfrac{2m}{2m - 1} > 0 \\2m - 1 < 0\end{matrix} \Rightarrow m < 0 \right.$

Vậy phương trình đã cho có nghiệm trong khoảng khi và chỉ khi .

Câu 2: Cho phương trình $x^{2} - 2mx + m^{2} - \frac{1}{2} = 0$ ( là tham số).

a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị .

b) Tìm để hai nghiệm của phương trình có giá trị tuyệt đối bằng nhau.

c) Tìm để hai nghiệm đó là số đo của 2 cạnh góc vuông của tam giác vuông có cạnh huyền bằng 3.

Hướng dẫn giải

a) $\ \Delta = (2m - 1)^{2} - 4 \cdot \left( m^{2} - 1 \right) = 5 - 4m$

Phương trình có hai nghiệm phân biệt $\Leftrightarrow m < \frac{5}{4}$

b) Phương trình hai nghiệm $\Leftrightarrow m < \frac{5}{4}$

Áp dụng hệ thức Vi-ét, ta có: $\left\{ \begin{matrix} x_{1} + x_{2} = 2m - 1 \\ x_{1}x_{2} = m^{2} - 1 \end{matrix} \right.$

Theo đề bài:

$\left( x_{1} - x_{2} \right)^{2} = x_{1} - 3x_{2}$

$\Leftrightarrow \left( x_{1} + x_{2} \right)^{2} - 4x_{1}x_{2} = x_{1} - 3x_{2}$

$\Leftrightarrow (2m - 1)^{2} - 4\left( m^{2} - 1 \right) = x_{1} - 3x_{2}$

$\Leftrightarrow x_{1} - 3x_{2} = 5 - 4m$

Ta có hệ phương trình: $\left\{\begin{matrix}x_{1} + x_{2} = 2m - 1 \\x_{1} - 3x_{2} = 5 - 4m\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x_{1} = \dfrac{m + 1}{2} \\x_{2} = \dfrac{3(m - 1)}{2}\end{matrix} \right.\ \right.$

$\begin{matrix} \Rightarrow \frac{{m + 1}}{2}.\frac{{3\left( {m - 1} \right)}}{2} = {m^2} - 1 \hfill \\ \Rightarrow 3\left( {{m^2} - 1} \right) = 4\left( {{m^2} - 1} \right) \hfill \\ \Rightarrow {m^2} - 1 = 0 \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = - 1 \hfill \\ \end{gathered} \right. \hfill \\ \end{matrix}$

Kết hợp với điều kiện đề bài suy ra $m = \pm 1$ là các giá trị cần tìm.

Câu 3: Cho phương trình $x^{2} - 2x + m + 3 = 0$ ( là tham số).

a) Tìm để phương trình có nghiệm . Tính nghiệm còn lại.

b) Tìm để hai nghiệm phân biệt $x_{1},x_{2}$ thỏa mãn hệ thức $x_{1}^{3} + x_{2}^{3} = 8$ .

Hướng dẫn giải

Ta có: $\Delta = 5^{2} - 4.1 \cdot (3m - 1) = 29 - 12m$

Để phương trình có hai nghiệm phân biệt $\Rightarrow \Delta \geq 0 \Rightarrow m \leq \frac{29}{12}$

Áp dụng hệ thức Vi-ét: $\left\{ \begin{matrix} x_{1} + x_{2} = - 5 \\ x_{1}x_{2} = 3m - 1 \end{matrix} \right.$

Ta có: $x_{1}^{3} - x_{2}^{3} + 3x_{1}x_{2} = 75$

$\Leftrightarrow \left( x_{1} - x_{2} \right)\left( \left( x_{1} + x_{2} \right)^{2} - x_{1}x_{2} \right) + 3x_{1}x_{2} = 75$

$\Rightarrow \left( x_{1} - x_{2} \right)\left( 25 - x_{1}x_{2} \right) + 3x_{1}x_{2} = 75$

$\Leftrightarrow 25\left( x_{1} - x_{2} \right) - \left( x_{1} - x_{2} \right)x_{1}x_{2} + 3x_{1}x_{2} = 75$

$\Rightarrow x_{1} - x_{2} = 3$

Kết hợp $x_{1} + x_{2} = - 5$ suy ra $x_{1} = - 1;x_{2} = - 4$

Thay vào $x_{1}x_{2} = 3m - 1$ suy ra $m = \frac{5}{3}$

Vậy $m = \frac{5}{3}$ là giá trị cần tìm

Câu 4: Tìm các giá trị của tham số để phương trình $x^{2} + (2m - 1)x + m^{2} - 1 = 0$ có hai nghiệm phân biệt $x_{1},x_{2}$ sao cho biểu thức $P = x_{1}^{2} + x_{2}^{2}$ đạt giá trị nhỏ nhất.

Hướng dẫn giải

a) Với phương trình đã cho trở thành $x^{2} - 10x + 9 = 0$

Ta có: nên phương trình có hai nghiệm phân biệt là $\left\lbrack \begin{matrix} x_{1} = 1 \\ x_{2} = 9 \end{matrix} \right.$

b) $\ \Delta' = ( - 5m)^{2} - 1.9m = 25m^{2} - 9m$

Điều kiện phương trình đã cho có hai nghiệm phân biệt là $\Delta' > 0$ $\Leftrightarrow 25m^{2} - 9m > 0\left( \ ^{*} \right)$

Theo hệ thức Vi-ét, ta có:

$\left\{ \begin{matrix} x_{1} + x_{2} = 10m \\ x_{1} - 9x_{2} = 0 \\ x_{1}x_{2} = 9m \end{matrix} \Leftrightarrow \left\{ \begin{matrix} 10x_{2} = 10m \\ x_{1} = 9x_{2} \\ x_{1}x_{2} = 9m \end{matrix} \right.\ \right.$

$\Leftrightarrow \left\{ \begin{matrix} x_{2} = m \\ x_{1} = 9m \\ 9m^{2} - 9m = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{2} = m \\ x_{1} = 9m,\left( \ ^{*} \right) \Rightarrow m = 1 \\ \left\lbrack \begin{matrix} m = 0 \\ m = 1 \end{matrix} \right.\ \end{matrix} \right.$

Câu 5: Cho phương trình $x^{2} - (m + 5)x + 2m + 6 = 0$ ( là ẩn số)

a) Chứng minh rằng: phương trình đã cho luôn luôn có hai nghiệm với mọi giá trị của .

b) Tìm để phương trình có hai nghiệm $x_{1},x_{2}$ thỏa mãn: $x_{1}^{2} + x_{2}^{2} = 35$ .

Hướng dẫn giải

a) Với phương trình đã cho trở thành $x^{2} - 2x - 1 = 0$

Ta có: $\Delta' = 2;x_{1,2} = 1 \pm \sqrt{2}$

Vậy với m = 0 phương trình đã cho có hai nghiệm phân biệt $x_{1,2} = 1 \pm \sqrt{2}$ .

b) Ta có: $\Delta' = m + 2$

Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi $\Delta' > 0 \Leftrightarrow m + 2 > 0 \Leftrightarrow m > - 2$

Áp dụng hệ thức Viète ta có: $\left\{ \begin{matrix} x_{1} + x_{2} = 2(m + 1) \\ x_{1}.x_{2} = m^{2} + m - 1 \end{matrix} \right.$

Do đó: $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 4 \Leftrightarrow \frac{x_{1} + x_{2}}{x_{1}.x_{2}} = 4 \Leftrightarrow \frac{2(m + 1)}{m^{2} + m - 1} = 4$

$\left\{ \begin{matrix} m^{2} + m - 1 \neq 0 \\ m + 1 = 2\left( m^{2} + m - 1 \right) \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} + m - 1 \neq 0 \\ 2m^{2} + m - 3 = 0 \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ m = - \frac{3}{2} \end{matrix} \right.$

Kết hợp với điều kiện suy ra $m \in \left\{ 1; - \frac{3}{2} \right\}$ là các giá trị cần tìm.

Câu 6: Cho phương trình $x^{2} + 2x + m - 2 = 0$ (1) ( là tham số)

a) Tìm để phương trình (1) có nghiệm.

b) Tìm để phương trình (1) có 2 là một nghiệm và tìm nghiệm còn lại.

Hướng dẫn giải

Để phương trình có hai nghiệm phân biệt $x_{1};x_{2}$ thì $\Delta > 0$

$\Leftrightarrow (2m - 1)^{2} - 4.2(m - 1) > 0$

$\Leftrightarrow 4m^{2} - 12m + 9 > 0$

$\Leftrightarrow (2m - 3)^{2} > 0 \Leftrightarrow m \neq \frac{3}{2}$

Mặt khác theo hệ thức Viète ta có:

$\begin{matrix}\left\{ \begin{matrix}x_{1} + x_{2} = \dfrac{2m - 1}{2} \\x_{1}.x_{2} = \dfrac{m - 1}{2}\end{matrix} \right.\ \\\end{matrix}$ $\Leftrightarrow \left\{ \begin{matrix}x_{1} = \dfrac{13 - 4m}{7} \\x_{2} = \dfrac{7m - 7}{26 - 8m} \\3.\dfrac{13 - 4m}{7} - 4.\dfrac{7m - 7}{26 - 8m} = 11\end{matrix} \right.$ .

Giải phương trình $3.\frac{13 - 4m}{7} - 4.\frac{7m - 7}{26 - 8m} = 11$ ta được các nghiệm $\left\lbrack \begin{matrix} m = - 1 \\ m = 4,125 \end{matrix} \right.$

Vậy $m \in \left\{ - 2;4,125 \right\}$ là các giá trị cần tìm.

Câu 7: Cho phương trình $x^{2} + mx + m - 1 = 0\ \ \ (1)$ với x là ẩn số.

a. Giải phương trình khi m = 2.

b. Chứng tỏ phương trình luôn có nghiệm với mọi giá trị của tham số m.

c. Gọi $x_{1};x_{2}$ là nghiệm của phương trình. Tính giá trị của biểu thức $A = \left( x_{1} + 1 \right)^{2}\left( x_{2} + 1 \right)^{2} + 2016$ .

Hướng dẫn giải

a. Phương trình đã cho có nghiệm khi và chỉ khi $\Delta' \geq 0$

$\Leftrightarrow \left\lbrack - (m - 1) \right\rbrack^{2} - 1\left( m^{2} - 3 \right) \geq 0$

$\Leftrightarrow - 2m + 4 \geq 0 \Leftrightarrow m \leq 2$

Vậy $m \leq 2$ thì phương trình đã cho có hai nghiệm.

b. Với $m \leq 2$ thì phương trình đã cho có hai nghiệm (chứng minh câu a)

Gọi một nghiệm của phương trình đã cho là thì nghiệm kia là

Theo hệ thức Viète ta có: $\left\{ \begin{matrix} x_{1} + x_{2} = 2m - 2 \\ x_{1}.x_{2} = m^{2} - 3 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} a + 3a = 2m - 2 \\ a.3a = m^{2} - 3 \end{matrix} \right.$

$\Leftrightarrow a = \frac{m - 1}{2} \Leftrightarrow 3\left( \frac{m - 1}{2} \right)^{2} = m^{2} - 3$

$\Leftrightarrow m^{2} + 6m - 15 = 0 \Leftrightarrow m = - 3 \pm 2\sqrt{6}(tm)$

Vậy $m = - 3 \pm 2\sqrt{6}$ là các giá trị cần tìm.

Câu 8: Cho phương trình $\frac{1}{2}x^{2} - mx + \frac{1}{2}m^{2} + 4m - 1 = 0$ ( là tham số).

a) Giải phương trình đã cho với .

b) Tìm để phương trình đã cho có hai nghiệm thỏa mãn $\frac{1}{x_{1}} + \frac{1}{x_{2}} = x_{1} + x_{2}$

Lời giải

a) Với phương trình trở thành $\frac{1}{x}x^{2} + x - \frac{9}{x} = 0$

$\Leftrightarrow x^{2} + 2x - 9 = 0$

$\Rightarrow \left\{ \begin{matrix} x_{1} = - 1 - \sqrt{10} \\ x_{2} = - 1 + \sqrt{10} \end{matrix} \right.$

b) Để phương trình đã cho có hai nghiệm phân biệt thì $\Delta > 0$

$\Leftrightarrow ( - m)^{2} - 4 \cdot \frac{1}{2} \cdot \left( \frac{1}{2}m^{2} + 4m - 1 \right) > 0$ $\Leftrightarrow - 8m + 2 > 0 \Leftrightarrow m < \frac{1}{4}$

Để phương trình có nghiệm khác $0 \Leftrightarrow \frac{1}{2}m^{2} + 4m - 1 \neq 0$

$\Rightarrow \left\{ \begin{matrix} m_{1} \neq - 4 - 3\sqrt{2} \\ m_{2} \neq - 4 + 3\sqrt{2} \end{matrix} \right.$

Ta có $\frac{1}{x_{1}} + \frac{1}{x_{2}} = x_{1} + x_{2}$ $\Leftrightarrow \left( x_{1} + x_{2} \right)\left( x_{1}x_{2} - 1 \right) = 0$

$\Leftrightarrow \left\{ \begin{matrix} x_{1} + x_{2} = 0 \\ x_{1}x_{2} - 1 = 0 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} 2m = 0 \\ m^{2} + 8m - 3 = 0 \end{matrix} \Leftrightarrow \left\{ \begin{matrix} m = 0 \\ m = - 4 - \sqrt{19} \\ m = - 4 + \sqrt{19} \end{matrix} \right.\ \right.$

Kết hợp với điều kiện ta được $\left\lbrack \begin{matrix} m = 0 \\ m = - 4 - \sqrt{19} \end{matrix} \right.$

Vậy $\left\lbrack \begin{matrix} m = 0 \\ m = - 4 - \sqrt{19} \end{matrix} \right.$ là các giá trị cần tìm.

Câu 9: Tìm tất cả các số tự nhiên để phương trình $x^{2} - m^{2}x + m + 1 = 0$ ( là tham số) có nghiệm nguyên.

Lời giải

$\Delta = \left( - m^{2} \right)^{2} - 4 \cdot 1 \cdot (m + 1) = m^{4} - 4m - 4$

Phương trình có nghiệm nguyên khi $\Delta = m^{4} - 4m - 4$ là số chính phương

Nếu $\left\lbrack \begin{matrix} m = 0 \\ m = 1 \end{matrix} \right.$ thì $\Delta < 0$ (loại)

Nếu thì $\Delta = 4 = 2^{2}$ (nhận)

Nếu $m \geq 3$ thì $2m(m - 2) > 5 \Leftrightarrow 2m^{2} - 4m - 5 > 0$

$\Leftrightarrow \Delta - \left( 2m^{2} - 4m - 5 \right) < \Delta < \Delta + 4m + 4$

$\Leftrightarrow m^{4} - 2m^{2} + 1 < \Delta < m^{4}$

$\Leftrightarrow \left( m^{2} - 1 \right)^{2} < \Delta < \left( m^{2} \right)^{2}$

$\Delta$ không là số chính phương.

Vậy là giá trị cần tìm

Câu 10: Cho phương trình $x^{2} - 2(m - 1)x + m - 3 = 0$ ( là tham số).

a) Chứng minh phương trình luôn có hai nghiệm phân biệt.

b) Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào .

c) Tìm giá trị nhỏ nhất của $P = x_{1}^{2} + x_{2}^{2}$ (với $x_{1},x_{2}$ là nghiệm của phương trình đã cho)

Lời giải

a) $\ \Delta' = \lbrack - (m - 1)\rbrack^{2} - 1 \cdot (m - 3) = m^{2} - 3m + 4 = \left( m - \frac{3}{2} \right)^{2} + \frac{7}{4} > 0,\ \forall m$

Vậy phương trình đã cho luôn có hai nghiệm phân biệt.
b) Theo hệ thức Vi-ét, ta có:

$\left\{ \begin{matrix} x_{1} + x_{2} = 2(m - 1) \\ x_{1}x_{2} = m - 3 \end{matrix} \Rightarrow \left\{ \begin{matrix} x_{1} + x_{2} = 2m - 2 \\ 2x_{1}x_{2} = 2m - 6 \end{matrix} \right.\ \right.$

$\Leftrightarrow x_{1} + x_{2} - 2x_{1}x_{2} - 4 = 0$ không phụ thuộc vào .

c) $P = x_{1}^{2} + x_{2}^{2} = \left( x_{1} + x_{2} \right)^{2} - 2x_{1}x_{2}$ $= 4(m - 1)^{2} - 2(m - 3)$

$= \left( 2m - \frac{5}{2} \right)^{2} + \frac{15}{4} \geq \frac{15}{4},\forall m$ Do đó $P_{\text{min~}} = \frac{15}{4}$ và dấu " " xảy ra khi $2m - \frac{5}{2} = 0 \Leftrightarrow m = \frac{5}{4}$

Vậy $P_{\min} = \frac{15}{4}$ vói $m = \frac{5}{4}$ .

Câu 13: Cho phương trình $x^{2} - (m + 1)x + m = 0$ ( là tham số). Gọi $x_{1}$ , $x_{2}$ là hai nghiệm của phương trình đã cho. Tìm giá trị của để $A = x_{1}^{2}x_{2} + x_{1}x_{2}^{2} + 2007$ đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.

Lời giải

Ta có $\Delta = \lbrack - (m + 1)\rbrack^{2} - 4m = m^{2} - 2m + 1 = (m - 1)^{2}$

Để phương trình có hai nghiệm phân biệt $\Delta > 0 \Rightarrow (m - 1)^{2} > 0 \Rightarrow m \neq 1$

Theo hệ thức Vi-ét, ta có: $\left\{ \begin{matrix} x_{1} + x_{2} = m + 1 \\ x_{1}x_{2} = m \end{matrix} \right.$

Ta có $A = x_{1}^{2}x_{2} + x_{1}x_{2}^{2} + 2007 = x_{1}x_{2}\left( x_{1} + x_{2} \right) + 2007$

$= m(m + 1) + 2007 = m^{2} + m + 2007$

$= m^{2} + 2 \cdot m \cdot \frac{1}{2} + \frac{1}{4} + 2006 + \frac{3}{4}$

$= \left( m + \frac{1}{2} \right)^{2} + \frac{8027}{4} \geq \frac{8027}{4},\forall m$

Dấu " " xảy ra $m + \frac{1}{2} = 0 \Leftrightarrow m = \frac{- 1}{2}$

Vậy $A_{\min} = \frac{8027}{4}$ với $m = - \frac{1}{2}$ .

Câu 14: Cho phương trình $x^{2} + 2mx + 2m - 1 = 0$ ( là tham số). Gọi $x_{1}$ , $x_{2}$ là hai nghiệm của phương trình đã cho. Tìm giá trị của để $A = x_{1}^{2}x_{2} + x_{1}x_{2}^{2}$ đạt giá trị lớn nhất.

Lời giải

Ta có $\Delta = (2m)^{2} - 4 \cdot 1 \cdot (2m - 1) = 4m^{2} - 8m + 4 = 4(m - 1)^{2}$

Để phương trình có hai nghiệm phân biệt $\Delta > 0 \Rightarrow (m - 1)^{2} > 0 \Rightarrow m \neq 1$

Theo hệ thức Vi-ét, ta có: $\left\{ \begin{matrix} x_{1} + x_{2} = - 2m \\ x_{1}x_{2} = 2m - 1 \end{matrix} \right.$

Ta có

$A = x_{1}^{2}x_{2} + x_{1}x_{2}^{2} = x_{1}x_{2}\left( x_{1} + x_{2} \right)$

$= - 4m^{2} + 2m = - 4\left( m^{2} - \frac{1}{2}m \right)$ $= - 4\left( m^{2} - 2 \cdot m \cdot \frac{1}{4} + \frac{1}{16} - \frac{1}{16} \right)$

$= - 4\left( m - \frac{1}{4} \right)^{2} + \frac{1}{4} \leq \frac{1}{4},\forall m$

Dấu " " xảy ra $m - \frac{1}{4} = 0 \Leftrightarrow m = \frac{1}{4}$

Vậy $A_{\max} = \frac{1}{4}$ với $m = \frac{1}{4}$ .

Câu 15: Cho phương trình $x^{2} - 2(m - 1)x + 2m - 5 = 0$ ( là tham số).

a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi .

b) Tìm giá trị của để phương trình có hai nghiệm $x_{1},x_{2}$ thỏa mãn $x_{1} < 1 < x_{2}$ .

Lời giải

a) Ta có $\Delta = \lbrack - 2(m - 1)\rbrack^{2} - 4 \cdot 1 \cdot (2m - 5) = 4m^{2} - 12m + 22$

$= (2m)^{2} - 2 \cdot 2m \cdot 3 + 9 + 13 = (2m + 3)^{2} + 13 > 0,\forall m$

Phương trình luôn có hai nghiệm phân biệt với mọi .

b) Theo hệ thức Vi-ét, ta có $\left\{ \begin{matrix} x_{1} + x_{2} = 2m - 2 \\ x_{1}x_{2} = 2m - 5 \end{matrix} \right.$

Theo giả thiết $x_{1} < 1 < x_{2} \Rightarrow \left\{ \begin{matrix} x_{1} - 1 < 0 \\ x_{2} - 1 > 0 \end{matrix} \Rightarrow \left( x_{1} - 1 \right)\left( x_{2} - 1 \right) < 0 \Rightarrow x_{1}x_{2} - \left( x_{1} + x_{2} \right) + 1 < 0 \right.$ (II)

Thay (I) vào (II) ta có:

$(2m - 5) - (2m - 2) + 1 < 0 \Leftrightarrow 0.m - 2 < 0$ , đúng vói mọi .

Vậy với mọi thì phương trình trên có hai nghiệm $x_{1},x_{2}$ thỏa mãn $x_{1} < 1 < x_{2}$ .

Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!

-----------------------------------------------------------------------

Ngoài Chuyên đề Phương trình bậc hai chứa tham số, mời các bạn học sinh tham khảo thêm các tài liệu Toán 9 khác trên VnDoc, các đề thi học kì 2 Toán 9 mà chúng tôi đã sưu tầm và chọn lọc. Với bài tập về chuyên đề Phương trình bậc hai chứa tham số này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!

Để giúp các bạn có thể giải đáp được những thắc mắc và trả lời được những câu hỏi khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt câu hỏi tại mục hỏi đáp học tập của VnDoc. Chúng tôi sẽ hỗ trợ trả lời giải đáp thắc mắc của các bạn trong thời gian sớm nhất có thể nhé.

Tải về

Chọn file muốn tải về:

Chuyên đề Phương trình bậc hai chứa tham số Toán 9 (Có đáp án)

235,3 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Bon

16

40.877

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!