Chứng minh ba đường thẳng đồng quy trong đường tròn
Chuyên đề thi vào lớp 10: Chứng minh 3 đường thẳng đồng quy
Chứng minh ba đường thẳng đồng quy là một dạng toán nâng cao trong đề thi tuyển sinh vào lớp 10 môn Toán được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.
- Ôn thi vào lớp 10 chuyên đề 10: Chứng minh các hệ thức hình học
- Các dạng Toán thi vào 10
- Các bài toán Hình học ôn thi vào lớp 10
Tài liệu dưới đây được VnDoc biên soạn gồm hướng dẫn giải chi tiết cho dạng bài "Chứng minh ba đường thẳng .... đồng quy" và tổng hợp các bài toán để các bạn học sinh có thể luyện tập thêm. Qua đó sẽ giúp các bạn học sinh ôn tập các kiến thức, chuẩn bị cho các bài thi học kì và ôn thi vào lớp 10 hiệu quả nhất. Sau đây mời các bạn học sinh cùng tham khảo tải về bản đầy đủ chi tiết.
I. Cách chứng minh ba đường thẳng đồng quy trong đường tròn
- Chứng minh một điểm đồng thời thuộc cả ba đường thẳng đó.
- Chứng minh giao điểm của hai đường thẳng này nằm trên đường thẳng thứ ba.
- Chứng minh giao điểm của hai đường thẳng thứ nhất và thứ hai trùng với giao điểm của hai đường thẳng thứ hai và thứ b.
- Sử dụng tính chất đồng quy của ba đường trung tuyến, đường cao, phân giác, trung trực trong tam giác.
- Sử dụng tính chất của đường chéo của các tứ giác đặc biệt.
II. Bài tập ví dụ cho bài toán chứng minh ba đường thẳng đồng quy trong đường tròn
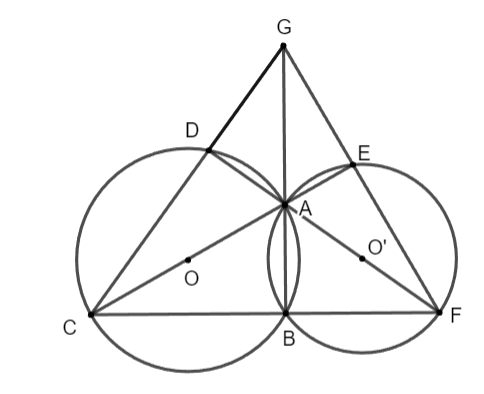
Bài 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Các đường thẳng AO và AO’ cắt (O) tại C và D và cắt (O’) tại E và F. Chứng minh rằng AB, CD, EF đồng quy.
Hướng dẫn giải
Hình vẽ minh họa
+ Có 
\(\widehat {ADC}\) nhìn đường kính AC nên \(\widehat {ADC} = {90^0}\)
+ Có \(\widehat {AEF}\) nhìn đường kính AF nên \(\widehat {AEF} = {90^0}\)
+ Có \(\widehat {ABC}\) nhìn đường kính AC nên \(\widehat {ABC} = {90^0}\)
+ Có \(\widehat {ABF}\) nhìn đường kính AF nên \(\widehat {ABF} = {90^0}\)
+ Có \(\widehat {ABC} + \widehat {ABF} = {90^0} + {90^0} = {180^0}\)
Suy ra 3 điểm E, B, F thẳng hàng
+ Xét tam giác CAF có các đường cao là AB, CD, EF nên AB, CD, EF đồng quy
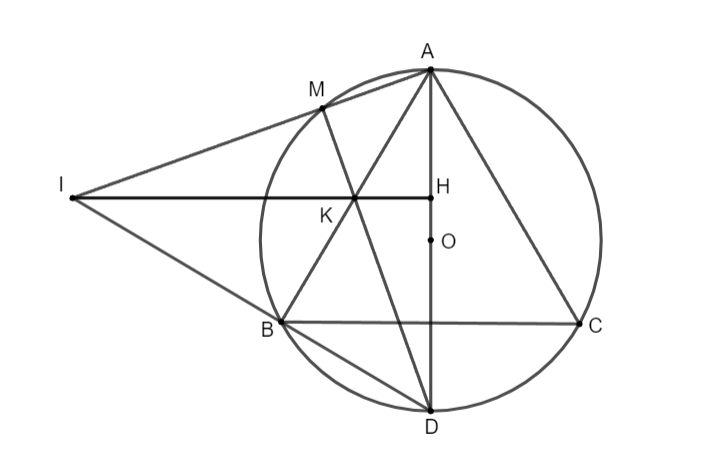
Bài 2: Cho tam giác đều ABC nội tiếp đường tròn đường kính AD. Gọi M là một điểm di động trên cung nhỏ AB (M không trùng với các điểm A và B). Gọi K là giao điểm của AB và MD, H là giao điểm của AD và MC. Chứng minh rằng ba đường thẳng AM, BD, HK đồng quy.
Hướng dẫn giải
Hình vẽ minh họa
+ Gọi I là giao điểm của AM và DB
+ Có \(\widehat {ABD} = \widehat {AMD}\left( { = {{90}^0}} \right)\)(2 góc nội tiếp đường tròn đường kính AD)
Suy ra AB và DM là hai đường cao của tam giác IAD
K là trực tâm của tam giác nên IK vuông góc với AD (1)
+ Có AC = AB (tam giác ABC đều) nên hai cung AC và AB bằng nhau \(\Rightarrow \widehat {AMC} = \widehat {ADB}\)
Góc \(\widehat {AMH}\) kề bù với góc \(\widehat {HMI}\) nên \(\widehat {HMI} + \widehat {HDI} = {180^0}\)
Suy ra tứ giác IMHD là tứ giác nội tiếp đường tròn đường kính ID
\(\Rightarrow \widehat {IMD} = \widehat {IHD}\left( { = {{90}^0}} \right)\)
Suy ra IH vuông góc với AD (2)
Từ (1) và (2) suy ra I, H, K thẳng hàng
Hay ba đường thẳng AM, BD và HK đồng quy ra I.
Bài 3: Cho đường tròn \((O)\) đường kính \(AB\), gọi \(I\) là trung điểm của \(OA\) và dây \(CD\) vuông góc với \(AB\) tại \(I\). Lấy \(K\) tùy ý trên cung nhỏ \(BC\), \(AK\) cắt \(CD\) tại \(H\).
a) Chứng minh tứ giác \(BIHK\) nội tiếp.
b) Chứng minh \(AH.AK\) có giá trị không phụ thuộc vị trí điểm \(K\).
c) Kẻ \(DN\bot BC;DM\bot AC;(N \in BC;M \in
AC)\). Chứng minh các đường thẳng \(AB;CD;MN\) đồng quy.
Hướng dẫn giải
Hình vẽ minh họa
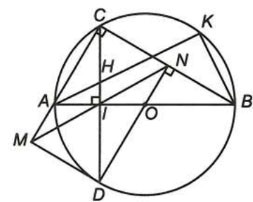
a) Xét tứ giác BIHK có \(\widehat{HIB} +
\widehat{HKB} = 180^{0}\)
Suy ra tứ giác BIHK nội tiếp đường tròn đường kính HB
b) Ta có: \(\Delta AHI\sim\Delta ABK(g -
g)\) vì góc HAI chung; \(\widehat{HIA}
= \widehat{AKB} = 90^{0}\)
\(\Rightarrow \frac{AH}{AB} = \frac{AI}{AK}
\Rightarrow AH.AK = AI.AB\) (không đổi)
c) Ta có: MD // CN (cùng vuông góc với MC)
AC // DN (cùng vuông góc với BC)
Suy ra MCND là hình bình hành.
Suy ra I là trung điểm của MN suy ra điều phải chứng minh.
Bài 4: Cho tam giác ABC vuông ở A. Trên cạnh AC lấy điểm M, dựng đường tròn (O) có đường kính MC. đường thẳng BM cắt đường tròn (O) tại D. đường thẳng AD cắt đường tròn (O) tại S.
1. Chứng minh ABCD là tứ giác nội tiếp.
2. Chứng minh CA là tia phân giác của góc SCB.
3. Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy.
5. Chứng minh DM là tia phân giác của góc ADE.
6. Chứng minh điểm M là tâm đường tròn nội tiếp tam giác ADE.
Hướng dẫn giải
Hình vẽ minh họa
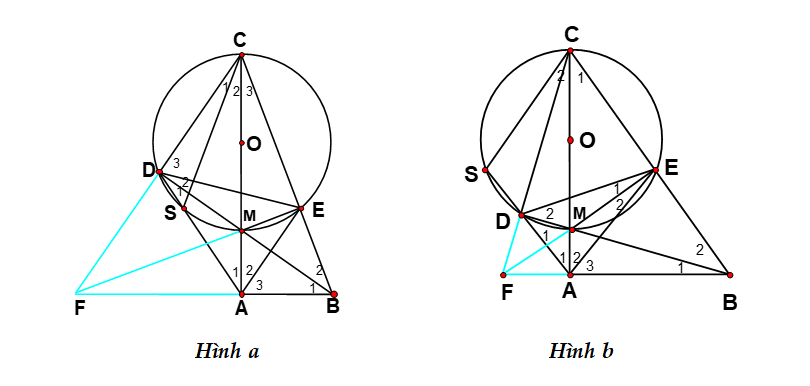
1. Ta có ∠CAB = 900 (vì tam giác ABC vuông tại A); ∠MDC = 900 (góc nội tiếp chắn nửa đường tròn) => ∠CDB = 900 như vậy D và A cùng nhìn BC dưới một góc bằng 900 nên A và D cùng nằm trên đường tròn đường kính BC => ABCD là tứ giác nội tiếp.
2. ABCD là tứ giác nội tiếp => ∠D1= ∠C3 (nội tiếp cùng chắn cung AB).
∠D1= ∠C3 => \(\stackrel\frown{SM}=\stackrel\frown{EM}\)=> ∠C2 = ∠C3 (hai góc nội tiếp đường tròn (O) chắn hai cung bằng nhau)
=> CA là tia phân giác của góc SCB.
3. Xét ∆CMB Ta có BA⊥CM; CD ⊥ BM; ME ⊥ BC như vậy BA, EM, CD là ba đường cao của tam giác CMB nên BA, EM, CD đồng quy.
4. Theo trên ta có: \(\stackrel\frown{SM}=\stackrel\frown{EM}\)=> ∠D1= ∠D2 => DM là tia phân giác của góc ADE. (1)
5. Ta có ∠MEC = 900 (nội tiếp chắn nửa đường tròn (O)) => ∠MEB = 900.
Tứ giác AMEB có ∠MAB = 900; ∠MEB = 900 => ∠MAB + ∠MEB = 1800 mà đây là hai góc đối nên tứ giác AMEB nội tiếp một đường tròn
=> ∠A2 = ∠B2
Tứ giác ABCD là tứ giác nội tiếp => ∠A1= ∠B2 ( nội tiếp cùng chắn cung CD)
=> ∠A1= ∠A2 => AM là tia phân giác của góc DAE (2)
Từ (1) và (2) Ta có M là tâm đường tròn nội tiếp tam giác ADE
TH2 (Hình b)
∠ABC = ∠CME (cùng phụ ∠ACB); ∠ABC = ∠CDS (cùng bù ∠ADC) => ∠CME = ∠CDS
=> \(\stackrel\frown{SM}=\stackrel\frown{EM}\)=> ∠SCM = ∠ECM => CA là tia phân giác của góc SCB.
Bài 5: Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì (H không trùng O, B); trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn; MA và MB thứ tự cắt đường tròn (O) tại C và D. Gọi I là giao điểm của AD và BC.
1. Chứng minh MCID là tứ giác nội tiếp .
2. Chứng minh các đường thẳng AD, BC, MH đồng quy tại I.
3. Gọi K là tâm đường tròn ngoại tiếp tứ giác MCID. Chứng minh KCOH là tứ giác nội tiếp.
Lời giải:
Hình vẽ minh họa;
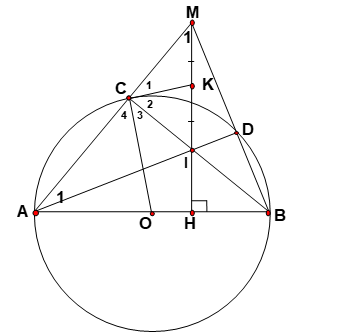
1. Ta có : ∠ACB = 900 ( nội tiếp chắn nửa đường tròn)
=> ∠MCI = 900 (vì là hai góc kề bù).
∠ADB = 900 ( nội tiếp chắn nửc đường tròn)
=> ∠MDI = 900 (vì là hai góc kề bù).
=> ∠MCI + ∠MDI = 1800 mà đây là hai góc đối của tứ giác MCID nên MCID là tứ giác nội tiếp.
2. Theo trên Ta có BC ⊥ MA; AD ⊥ MB nên BC và AD là hai đường cao của tam giác MAB mà BC và AD cắt nhau tại I nên I là trực tâm của tam giác MAB. Theo giả thiết thì MH ⊥ AB nên MH cũng là đường cao của tam giác MAB
=> AD, BC, MH đồng quy tại I.
3. ∆OAC cân tại O ( vì OA và OC là bán kính) => ∠A1 = ∠C4
∆KCM cân tại K ( vì KC và KM là bán kính) => ∠M1 = ∠C1 .
Mà ∠A1 + ∠M1 = 900 ( do tam giác AHM vuông tại H) => ∠C1 + ∠C4 = 900 => ∠C3 + ∠C2 = 900 ( vì góc ACM là góc bẹt) hay ∠OCK = 900 .
Xét tứ giác KCOH Ta có ∠OHK = 900; ∠OCK = 900 => ∠OHK + ∠OCK = 1800 mà ∠OHK và ∠OCK là hai góc đối nên KCOH là tứ giác nội tiếp.
Bài 6: Cho đường tròn (O; R) và (O’; R’) có R > R’ tiếp xúc ngoài nhau tại C. Gọi AC và BC là hai đường kính đi qua điểm C của (O) và (O’). DE là dây cung của (O) vuông góc với AB tại trung điểm M của AB. Gọi giao điểm thứ hai của DC với (O’) là F, BD cắt (O’) tại G. Chứng minh rằng:1. Tứ giác MDGC nội tiếp .
2. Bốn điểm M, D, B, F cùng nằm trên một đường tròn
3. Tứ giác ADBE là hình thoi.
4. B, E, F thẳng hàng
5. DF, EG, AB đồng quy.
6. MF = 1/2 DE.
7. MF là tiếp tuyến của (O’).
Lời giải:
Hình vẽ minh họa:
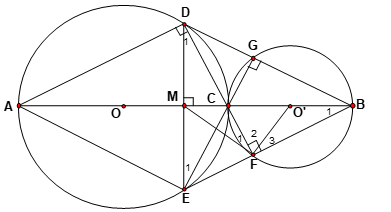
1. ∠BGC = 900 ( nội tiếp chắn nửa đường tròn)
=> ∠CGD = 900 (vì là hai góc kề bù)
Theo giả thiết DE ⊥ AB tại M => ∠CMD = 900
=> ∠CGD + ∠CMD = 1800 mà đây là hai góc đối của tứ giác MCGD nên MCGD là tứ giác nội tiếp
2. ∠BFC = 900 ( nội tiếp chắn nửa đường tròn)
=> ∠BFD = 900; ∠BMD = 900 (vì DE ⊥ AB tại M) như vậy F và M cùng nhìn BD dưới một góc bằng 900 nên F và M cùng nằm trên đường tròn đường kính BD
=> M, D, B, F cùng nằm trên một đường tròn .
3. Theo giả thiết M là trung điểm của AB; DE ⊥ AB tại M nên M cũng là trung điểm của DE (quan hệ đường kính và dây cung)
=> Tứ giác ADBE là hình thoi vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
4. ∠ADC = 900 ( nội tiếp chắn nửa đường tròn ) => AD ⊥ DF ; theo trên tứ giác ADBE là hình thoi
=> BE // AD mà AD ⊥ DF nên suy ra BE ⊥ DF .
Theo trên ∠BFC = 900 ( nội tiếp chắn nửa đường tròn ) => BF ⊥ DF mà qua B chỉ có một đường thẳng vuông góc với DF do đo B, E, F thẳng hàng.
5. Theo trên DF ⊥ BE; BM ⊥ DE mà DF và BM cắt nhau tại C nên C là trực tâm của tam giác BDE
=> EC cũng là đường cao => EC⊥BD; theo trên CG⊥BD
=> E, C, G thẳng hàng. Vậy DF, EG, AB đồng quy
6. Theo trên DF ⊥ BE => ∆DEF vuông tại F có FM là trung tuyến (vì M là trung điểm của DE) suy ra
MF = 1/2 DE ( vì trong tam giác vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền).
7. (HD) theo trên MF = 1/2 DE => MD = MF => ∆MDF cân tại M => ∠D1 = ∠F1
∆O’BF cân tại O’ ( vì O’B và O’F cùng là bán kính )
=> ∠F3 = ∠B1 mà ∠B1 = ∠D1 (Cùng phụ với ∠DEB )
=> ∠F1 = ∠F3 => ∠F1 + ∠F2 = ∠F3 + ∠F2 . Mà ∠F3 + ∠F2 = ∠BFC = 900
=> ∠F1 + ∠F2 = 900 = ∠MFO’ hay MF ⊥ O’F tại F => MF là tiếp tuyến của (O’).
III. Bài tập tự luyện về bài toán chứng minh ba đường thẳng đồng quy trong đường tròn
Bài 1: Cho tam giác ABC vuông tại A trên cạnh AC lấy M vẽ đường tròn đường kính MC tâm O. Đường thẳng BM cắt đường tròn O tại D. Đường thẳng AD cắt đường tròn O tại S. Gọi E là giao điểm của BC của đường tròn O. Chứng minh: BA , EM , CD đồng quy
Bài 2: Cho nửa đường tròn O, đường kính AB = R, bán kính OC vuông góc AB. M là một điểm trên cung nhỏ BC, AM cắt CO tại N
a) Chứng minh tứ giác BMN nội tiếp đường tròn
b) Chứng minh AM.AN = 2R2
c) Kéo dài BN cắt nửa đường tròn tại K. Chứng minh ba đường thẳng AC, BM, ON đồng quy
Bài 3: Cho nửa đường tròn tâm O đường kính AB. Từ A, B vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Từ M là điểm trên nửa đường tròn (O) (M không là điểm chính giữa cung AB) vẽ tiếp tuyến lần lượt cắt Ax, By tại điểm C, D.
a) Chứng tỏ AC + BD = CD
b) Chứng minh tam giác COD vuông
c) Tia BM cắt Ax tại P, tia AM cắt By tại Q. Chứng minh ba đường thẳng AB, CD, PQ đồng quy.
Bài 4: Cho tam giác ABC vuông ở A. 1 điểm D nằm giữa A và B, đường tròn đường kính BD cắt BC tại E. Các đường thẳng CD, AE cắt đường tròn tại F, G. Chứng minh:
a, Hai tam giác ABC và EBD đồng dạng với nhau
b, Tứ giác ADEC và tứ giác AFBC nội tiếp đường tròn
c, AC // FG
d, Các đường thẳng AC, DE và BF đồng quy
-------------------
Ngoài các dạng Toán 9 ôn thi vào lớp 10 trên, mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt!
