Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 9 Toán 9 Chuyên đề Toán 9

Chuyên đề hệ thức lượng trong tam giác vuông

Bài tập hình học lớp 9 ôn thi vào 10
Lớp: Lớp 9
Môn: Toán
Loại File: PDF
Phân loại: Tài liệu Tính phí
Bài 1. Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường
cao. Tính BH, CH, AC và AH.
Bài 2. Cho tam giác ABC vuông tại A có AC = 10cm, AB = 8cm. AH là đường
cao. Tính BC, BH, CH, AH.
HD:BC=2
; BH=32
/41 ; CH=50
/41; AH=40
/41.
Bài 3. Cho tam giác ABC vuông tại A có BC = 12cm. Tính chiều dài hai cạnh
góc vuông biết
Bài 4. Cho tam giác ABC vuông tại A có đường cao AH. Biết BH=10cm, CH=42
cm. Tính BC, AH, AB và AC.
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

1 1 1
2 2 2
AH AB AC
..
AB AC BC AH
.
2
.
AH BH CH
2
.
;
AC BC CH
2
AB BC BH

2 2 2
Định lí Pi-ta-go:
BC AB AC
HD:
BC cm52
,
AH cm2 105
,
AB cm2 130
,
AC cm2 546
.
.
()
13
36 13
,
AC cm
()
13
24 13
HD:
AB cm
AB AC
.
2
3
HD:
BH cm1,8
,
CH cm3,2
,
AC cm4
,
AH cm2,4
.
Bài 5. Hình thang cân ABCD có đáy lớn AB = 30cm, đáy nhỏ CD = 10cm và góc
A là
0
60
a) Tính cạnh BC. b) Gọi M, N lần lượt là trung điểm AB và
CD. Tính MN.
HD:
a, Gọi P và Q là chân đường cao kẻ từ D và C xuống AB: AP=QB mà
PQ=DC=10cm nên AP=QB=(30-10):2=10cm.
b, NM=DP=AP. =10 cm.
I. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
Cho tam giác ABC vuông tại A, đường cao AH.
Tải tài liệu học tập, văn bản pháp luật, biểu mẫu miễn phí tại VnDoc
và D đến AC. c)Tính HK. d) Vẽ BE DC kéo dài. Tính BE,
CE và DC.
HD:
a, BD
2
=AB
2
+AD
2
=> BD=10
cm.
b,
ABC đều (AB=AC mà
) nên BH=5
cm,
ADK có
nên KD=1/2AD=5cm,
c, ABH có
nên AH=1/2AB=5cm, mà AK
2
=AD
2
-DK
2
=75 nên
AK=5
cm
suy ra HK=5
-5 cm.
d,
ADC cân có
nên
=>
nên
BEC vuông cân tại E nên BE=EC mà BE
2
+EC
2
=BC
2
=>
BE=EC=5
cm.
90
a) Tính đường chéo BD. b) Tính các khoảng cách BH và DK từ B
60
và góc
A là
0
Bài 6. Cho tứ giác lồi ABCD có AB = AC = AD = 10cm, góc B bằng
0
Trong KDC có KD=5cm, KC=AC-AK=10-5 cm Dùng pytago tính DC.
Bài 7. Cho đoạn thẳng AB=2a. Từ trung điểm O của AB vẽ tia Ox AB. Trên
Ox, lấy điểm D sao cho
a
OD
2
. Từ B kẻ BC vuông góc với đường thẳng AD.a)
Tính AD, AC và BC theo a.b) Kéo dài DO một đoạn OE = a. Chứng minh
bốn điểm A, B, C và E cùng nằm trên một đường tròn.
HD:
a, AD=
ADO
ABC nên AD.AC=AB.AO => AC= Dùng pytago cho
tam giác ABC để tính BC= .
b, Chỉ ra OA=OB=OC=OE.
Tải tài liệu học tập, văn bản pháp luật, biểu mẫu miễn phí tại VnDoc
Bài 8. Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Trên
HB và HC lần lượt lấy các điểm M, N sao cho góc AMC= góc ANB=90
0
.
Chứng minh: AM = AN.
Bài 9. Cho tam giác ABC vuông tại A, đường cao AH. Biết
420. Tính chu vi tam giác ABC.
Bài 10. Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc

, tính diện tích hình thang ABCD.
Tính được: OB = 4, OD = 9, OC = 13,5.HD:
S 126,75
.
với nhau tại O. Biết
AB OA2 13, 6
P 2030
.
ABC
HD:Đặt
AB k AC k BC k20 , 21 29
. Từ AH.BC = AB.AC
k 29
.HD:
21
và AH =
20AB
AC
..
.
22
HD:
ABD
ACE
AM AC AD AB AE AN
caïnh ñoái
caïnh huyeàn
sina
;
caïnh keà
caïnh huyeàn
cosa
;
caïnh ñoái
caïnh keà
tana
;
caïnh keà
caïnh ñoái
cota
Chú ý:
, hoặc
2. Tỉ số lượng giác của hai góc phụ nhau:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng
cotang góc kia.
Sin (90
0
-a) = cosa tan(90
0
-a)=cotana
cos(90
0
-a)=sina cotan(90
0
-a)=tana
Ví dụ: sin 25
0
=cos65
0
; tan20
0
=cotan70
0
…..
3. Tỉ số lượng giác của các góc đặc biệt:
II. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1. Định nghĩa: Cho tam giác vuông có góc nhọn
.
ab
. ) thì
ab
, hoặc
cot cotabtan tan

(hoặc
cos cos
ab
Cho 2 góc nhọn
,
. Nếu
sin sin

.
Cho góc nhọn
. Ta có:
0 sin 1; 0 cos 1
Tải tài liệu học tập, văn bản pháp luật, biểu mẫu miễn phí tại VnDoc

Chuyên đề hệ thức lượng trong tam giác vuông

Bài tập ôn tập hệ thức lượng trong tam giác vuông Toán lớp 9 được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

Trong chương trình Hình học 9, chuyên đề hệ thức lượng trong tam giác vuông là một mảng kiến thức quan trọng, thường xuyên xuất hiện trong các đề kiểm tra và đề thi vào lớp 10. Nắm vững hệ thức lượng không chỉ giúp học sinh giải nhanh các bài toán về tam giác vuông, mà còn là nền tảng để tiếp cận các chuyên đề hình học nâng cao. Bài viết này sẽ tổng hợp lý thuyết trọng tâm, công thức cơ bản và bộ bài tập hệ thức lượng trong tam giác vuông có lời giải chi tiết, giúp học sinh ôn tập hiệu quả và tự tin hơn khi làm bài tập hình học lớp 9 ôn thi vào 10.

Ngoài ra chúng tôi cung cấp các chuyên đề luyện thi vào 10 mà chúng tôi đã sưu tầm và chọn lọc như:

Với bài tập trong bộ đề cương này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!

I. Một số hệ thức về cạnh và đường cao trong tam giác vuông

Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ):

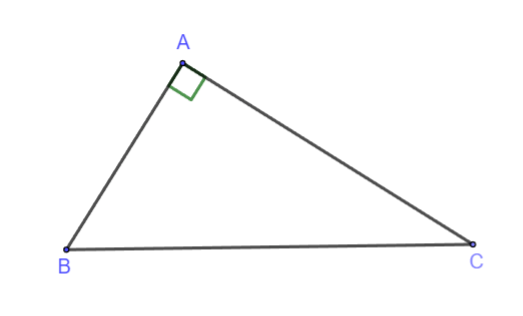
Định lý Pythagore: BC^{2} = AB^{2} + AC^{2}

AB^{2} = BC.BH                                       AC^{2} = BC.CH

AH^{2} = BH.CH                    AB.AC = BC.AH                 \frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}}

II. Tỉ số lượng giác của góc nhọn

1. Định nghĩa tỉ số lượng giác

Hình vẽ minh họa

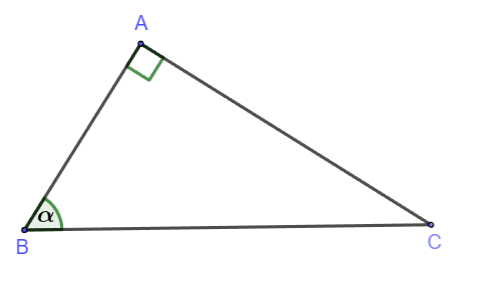
Cho tam giác vuông có góc nhọn \widehat{ABC} = \alpha ta có:

\sin\alpha = \frac{AC}{BC};cos\alpha = \frac{AB}{BC}

\tan\alpha = \frac{AC}{AB};cot\alpha = \frac{AB}{AC}

2. Tỉ số lượng giác của hai góc phụ nhau

Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.

\sin\left( 90^{0} - \alpha \right) = \cos\alpha                       \cos\left( 90^{0} - \alpha \right) = \sin\alpha

\tan\left( 90^{0} - \alpha \right) = \cot\alpha                      \cot\left( 90^{0} - \alpha \right) = \tan\alpha

3. Tỉ số lượng giác của các góc đặc biệt

Bảng tỉ số lượng giác của các góc đặc biệt:

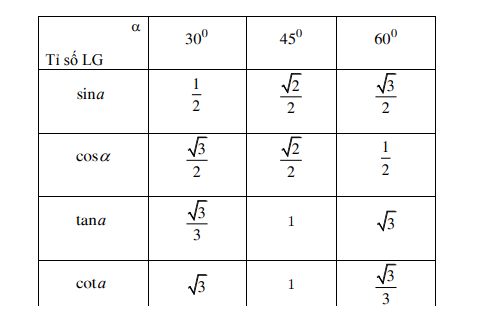
4. Một số hệ thức lượng giác quan trọng

\tan\alpha = \frac{\sin\alpha}{\cos\alpha}                                     \cot\alpha = \frac{\cos\alpha}{\sin\alpha}

\tan\alpha.cot\alpha = 1                                   sin^{2}\alpha + cos^{2}\alpha = 1

1 + tan^{2}\alpha = \frac{1}{cos^{2}\alpha}                           1 + cot^{2}\alpha = \frac{1}{sin^{2}\alpha}

5. Công thức diện tích tam giác

Hình vẽ minh họa:

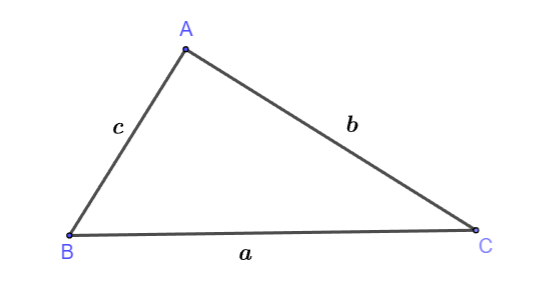
S_{\Delta ABC} = \frac{1}{2}ab.sin\widehat{C} = \frac{1}{2}bc.sin\widehat{A} = \frac{1}{2}ac.sin\widehat{B}

Phát biểu thành lời: Diện tích tam giác bằng một nửa tích hai cạnh kề với sin góc xen giữ hai cạnh đó.

S_{\Delta ABC} = p.r = \frac{abc}{4R}

R là bán kính đường tròn ngoại tiếp tam giác ABC

R là bán kính đường tròn nội tiếp tam giác ABC.

Trong tam giác bất kì ta có: \frac{b}{\sin\widehat{B}} = \frac{a}{\sin\widehat{A}} = \frac{c}{\sin\widehat{C}}

III. Một số hệ thức về cạnh và góc trong tam giác vuông

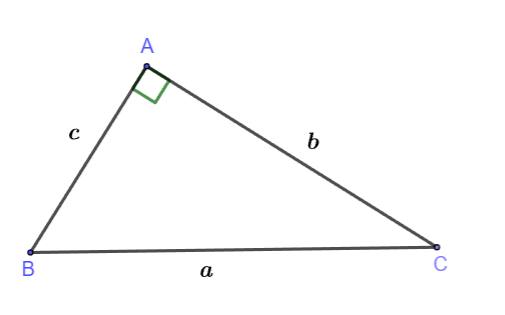
Cho tam giác ABC vuông tại A (như hình vẽ):

b = a.sin\widehat{B} = a.cos\widehat{C}                        c = a.sin\widehat{C} = a.cos\widehat{B}

b = c.tan\widehat{B} = c.cot\widehat{C}                          c = b.tan\widehat{C} = b.cot\widehat{B}

Không thể hiển thị hết nội dung tại đây — bấm Tải về để lấy toàn bộ tài liệu.

---------------------------------------------------------

Chuyên đề hệ thức lượng trong tam giác vuông không chỉ củng cố kiến thức hình học cơ bản mà còn rèn luyện kỹ năng tư duy logic, khả năng vận dụng linh hoạt công thức vào nhiều dạng toán khác nhau. Với hệ thống lý thuyết súc tích và các dạng bài tập minh họa có đáp án chi tiết, học sinh hoàn toàn có thể tự học và nâng cao năng lực giải toán hình học. Đây cũng là tài liệu hữu ích cho quá trình ôn tập dài hạn, giúp học sinh chuẩn bị vững chắc cho kỳ thi tuyển sinh vào lớp 10 môn Toán. Hãy luyện tập thường xuyên, kết hợp lý thuyết và bài tập, chắc chắn các em sẽ đạt được kết quả học tập như mong muốn.

Chọn file muốn tải về:

Chuyên đề hệ thức lượng trong tam giác vuông

361,8 KB
Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!
Đóng
79.000 / tháng
Mua ngay
Đặc quyền các gói Thành viên
PRO
Phổ biến nhất
PRO+
Tải tài liệu Cao cấp 1 Lớp
30 lượt tải tài liệu
Xem nội dung bài viết
Trải nghiệm Không quảng cáo
Làm bài trắc nghiệm không giới hạn
Mua cả năm Tiết kiệm tới 48%
50
56.479 Bài viết đã được lưu
Mục lục

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này

Tham khảo thêm

🖼️

Đề thi vào 10 môn Toán
Xem thêm
🖼️

Gợi ý cho bạn
Xem thêm