Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Bài tập nâng cao hàm số y=ax^2

Bài tập nâng cao Toán 9

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Đề thi HSG

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập nâng cao hàm số

Bài tập nâng cao hàm số Toán lớp 9 do thư viện đề thi VnDoc.com sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Đây là phần bài tập nâng cao giúp cho các bạn học sinh ôn tập, củng cố kiến thức và rèn luyện kĩ năng làm bài Toán.

Phần lý thuyết sẽ nhắc lại ngắn gọn nội dung của bài học: Hàm số
Phần bài tập sẽ đưa ra một số dạng bài tập nâng cao với ví dụ có lời giải và bài tập vận dụng.
Qua đó sẽ giúp các bạn học sinh củng cố lại kiến thức về bài tập đã học trên lớp đồng thời giúp các bạn nâng cao thêm kỹ năng giải Toán.

A. Hàm số bậc hai

1. Tập xác định của hàm số bậc hai

Hàm số $y=ax^2 (a\hspace{0,2cm} \text{khác} \hspace{0,2cm}0)$ xác định với mọi x thuộc R.

2. Tính chất của hàm số bậc hai

+ Nếu a>0 thì hàm số nghịch biến với x<0, đồng biến với x>0, bằng 0 với x=0.

+ Nếu a<0 thì hàm số đồng biến với x<0, nghịch biến với x>0, bằng 0 với x=0.

3. Đồ thị hàm số bậc hai

Đồ thị của hàm số là một parabol đi qua gốc tọa độ và nhận trục tung làm trục đối xứng.

Nhận xét

+ Nếu a>0 thì y>0 với mọi x khác 0. Khi x=0, giá trị nhỏ nhất của hàm số là y=0.

+ Nếu a<0 thì y<0 với mọi x khác 0. Khi x=0, giá trị lớn nhất của hàm số là y=0.

B. Bài tập nâng cao hàm số bậc hai

Ví dụ 1: Cho parabol $y=\frac{1}{4}x^2$ , điểm A(0;1) và đường thẳng có phương trình y= -1. Gọi M là một điểm bất kì thuộc parabol. Chứng minh rằng MA bằng khoảng cách MH từ điểm M đến đường thẳng d.

Hướng dẫn giải chi tiết

Hình vẽ minh họa

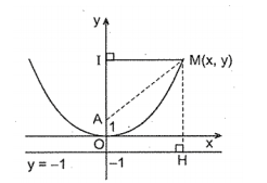
Gọi điểm là một điểm bất kì thuộc parabol. Khoảng cách từ điểm tới bằng . Do đó ta luôn có .

Goi là hình chiếu của lên trục . Kh đó ta có

Điểm $A(0;a) \Rightarrow AI = |y - 1|$

Áp dụng định lý Pytago có: $MA^{2} = MI^{2} + AI^{2} = x^{2} + (y - 1)^{2} = x^{2} + y^{2} - 2y + 1$

Do $y = \frac{1}{4}x^{2}$ nên thay $x^{2}$ bởi ta được

$MA^{2} = 4y + y^{2} - 2y^{2} + 1 = (y + 1)^{2} \Rightarrow MA = |y + 1|$

Mà $a = \frac{1}{4} > 0$ nên $y \geq 0$ do đó .

Từ (1) và (2) ta có .

Ví dụ 2: Cho điểm A(0;a), gọi d là đường thẳng có phương trình y= -a. Chứng minh rằng quỹ tích của điểm M(x;y) sao cho khoảng cách MH từ M tới d bằng là một parabol.

Hướng dẫn giải chi tiết

Hình vẽ minh họa

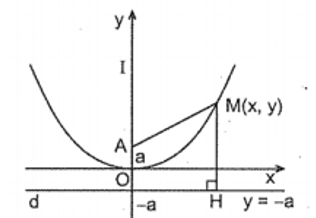
Theo công thức tính khoảng cách giữa hai điểm và ta có

$MA^{2} = (x - 0)^{2} + (y - a)^{2} = x^{2} + y^{2} - 2ay + a^{2}$

Lại có khoảng cách hay $MH^{2} = (y + a)^{2} = y^{2} + 2ay + a^{2}$

Theo đề bài $MA^{2} = MH^{2}$

$\Leftrightarrow x^{2} + y^{2} - 2ay + a^{2} = y^{2} + 2ay + a^{2} \Leftrightarrow x^{2} = 4ay \Leftrightarrow y = \frac{1}{4a}x^{2}$

Do đó quý tích của là parabol $y = \frac{1}{4a}x^{2}$ .

Chú ý: Tổng quát, cho điểm A và đường thẳng d không đi qua A, quỹ tích các điểm M sao cho khoảng cách MA bằng khoảng cách từ M đến d là một parabol. Khi đó điểm A gọi là tiêu điểm, đường thẳng d gọi là đường chuẩn của parabol.

C. Bài tập áp dụng

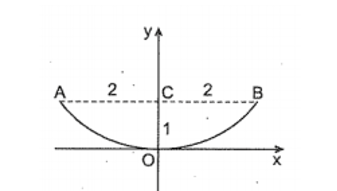
Bài 1: Thiết diện đi qua trục của một chiếc bát có dạng parabol. Hãy xác định phương trình của parabol đó, biết rằng độ sâu OC = 1cm và đường kính AB = 4cm.

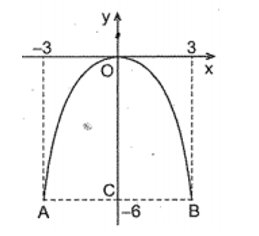
Bài 2: Một cổng dạng parabol có kích thước là OC = 6m, AB = 6m. Viết phương trình của parabol ấy.

Bài 3: Vẽ đồ thị của hàm số $y = \frac{1}{3}x|x|$ .

Bài 4: Tìm tọa độ của điểm M thuộc parabol $y = ax^{2}$ (parabol này đi qua điểm ), biết khoảng cách ta M đến trục hoành gấp đôi khoảng cách từ M đến trục tung.

Bài 5: Gọi C là một điểm tùy ý nằm trên parabol $y = - \frac{1}{2}x^{2}$ . Gọi K là trung điểm của OC. Khi điểm C di chuyển trên parabol đó thì điểm K di chuyển trên đường nào?

(Để xem tiếp tài liệu mời tải tài liệu về)

Bài 6. Cho hàm số $y = (2m - 1)x^{2}$ (với là tham số). Biết rằng thỏa mãn $\left\{ \begin{matrix} x + y = 2 \\ x^{2} - 2y = - 4 \end{matrix} \right.$ . Tổng tất cả các giá trị của tham số khi đó bằng bao nhiêu?

Bài 7. Một người thực hiện nhảy dù ở độ cao so với mực nước biển. Quãng đường chuyển động (đơn vị: mét) phụ thuộc vào thời gian (đơn vị: giây) được xác định bởi công thức $S = 5t^{2}$ . Hỏi sau khoảng thời gian , người đó cách mặt đất bao nhiêu mét?

Bài 8. Một người thực hiện nhảy dù ở độ cao so với mực nước biển. Quãng đường chuyển động (đơn vị: mét) phụ thuộc vào thời gian (đơn vị: giây) được xác định bởi công thức $S = 5t^{2}$ . Sau khoảng thời gian bao lâu thì người đó cách mặt đất ?

Bài 9. Động năng của một quả sầu riêng rơi được tính bằng công thức $W_{d} = \frac{mv^{2}}{2}$ với là khối lượng quả sầu riêng , là vận tốc của sầu riêng . Tính vận tốc rơi của quả sầu riêng nặng thời điểm quả sầu riêng đạt động năng ?

Hướng dẫn đáp án

Bài 6.

Xét hệ phương trình $\left\{ \begin{matrix} x + y = 2 \\ x^{2} - 2y = - 4 \end{matrix} \right.$ như sau:

$\left\{ \begin{matrix} x + y = 2 \\ x^{2} - 2y = - 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} 2x + 2y = 4 \\ x^{2} - 2y = - 4 \end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix} x^{2} + 2x = 0 \\ x + y = 2 \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \Rightarrow y = 2 \\ x = - 2 \Rightarrow y = 4 \end{matrix} \right.$

Thay vào hàm số $y = (2m - 1)x^{2}$ ta được:

(vô lí)

Thay vào hàm số $y = (2m - 1)x^{2}$ ta được:

$4 = (2m - 1).( - 2)^{2} \Leftrightarrow m = 1$ .

Vậy tổng tất cả các giá trị m thỏa mãn yêu cầu bằng 1.

Bài 7.

Sau người đó rơi được quãng đường là $S = 5.4^{2} = 80(m)$

Suy ra người đó cách mặt đất một khoảng là .

----------------------------------------------------

Ngoài Bài tập nâng cao hàm số , mời các bạn học sinh tham khảo thêm các tài liệu ôn thi học sinh giỏi Toán 9 như 40 đề luyện thi học sinh giỏi Toán 9, Đề thi học sinh giỏi cấp huyện lớp 9 môn Toán Phòng GD&ĐT Tân Kỳ, Nghệ An năm học 2019 - 2020... mà chúng tôi đã sưu tầm và chọn lọc. Với Bài tập nâng cao hàm số của chương 4 Toán 9 này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt!

Tải về

Chọn file muốn tải về:

Bài tập nâng cao hàm số y=ax^2

436,2 KB

Tải tài liệu định dạng .doc
352 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Lê Hằng Anh

4.975

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!