Bài tập Góc có đỉnh nằm bên trong, góc có đỉnh bên ngoài đường tròn Toán 9 Có đáp án
Bài tập Toán 9 góc trong và ngoài đường tròn có đáp án
Trong chương trình Toán lớp 9, phần hình học liên quan đến góc có đỉnh nằm bên trong và góc có đỉnh nằm bên ngoài đường tròn là một nội dung quan trọng, thường xuyên xuất hiện trong các đề kiểm tra và thi học kỳ. Tuy nhiên, nhiều học sinh còn nhầm lẫn giữa các công thức tính và cách nhận dạng từng loại góc. Bài viết dưới đây sẽ giúp bạn hệ thống kiến thức lý thuyết và luyện tập với các bài tập góc có đỉnh bên trong và bên ngoài đường tròn có đáp án chi tiết, dễ hiểu, hỗ trợ hiệu quả trong việc học và ôn thi.
A. Kiến thức cần nhớ
1. Góc có đỉnh nằm bên trong đường tròn
a. Định nghĩa
Góc có đỉnh nằm bên trong đường tròn là góc có đỉnh là giao điểm của hai dây cung (hoặc tiếp tuyến) và giao điểm nay nằm bên trong đường tròn. Hai cung nằm bên trong góc gọi là hai cung bị chắn.
+ 
\(\widehat{BAC}\) là góc có đỉnh nằm trong đường tròn, góc này chắn hai cung là BC và MN.
b. Tính chất
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng hai cung bị chắn. Nghĩa là \(\widehat{BAC} =
\frac{1}{2}\left( sđ\widehat{BC} + sđ\widehat{MN} \right)\)
2. Góc có đỉnh nằm bên ngoài đường tròn
a. Định nghĩa
Góc có đỉnh nằm bên ngoài đường tròn là góc có đỉnh là giao điểm của hai dây cung (hoặc tiếp tuyến) và giao điểm nay nằm bên ngoài đường tròn. Hai cung nằm bên trong góc gọi là hai cung bị chắn.
+ \(\widehat{BAC}\) là góc có đỉnh nằm ngoài đường tròn, góc này chắn hai cung là BC và DE
b. Tính chất
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu hai cung bị chắn. Nghĩa là \(\widehat{BAC} =
\frac{1}{2}\left( sđ\widehat{DE} - sđ\widehat{BC} \right)\)
B. Bài tập Góc có đỉnh bên trong, bên ngoài đường tròn
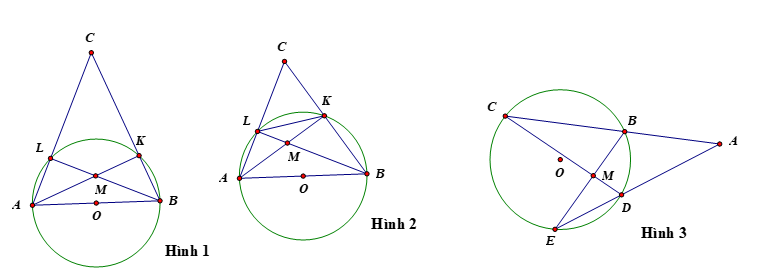
Câu 1 Trong hình 1, Biết số đo cung LK bằng 1000 thì số đo góc C bằng
A. 300. B. 400. C. 450. D. 500
Câu 2 Trong hình 1 Biết số đo cung LK bằng 1000 thì số đo góc AMB bằng
A. 1200. B. 1400. C. 1450. D. 1600
Câu 3 Trong hình 2, cho đường tròn (O; R), dây cung LK = R thì số đo góc C bằng
A. 500. B. 1000. C. 600. D. 400
Câu 4 Trong hình 2, cho đường tròn (O; R), dây cung LK = R thì số đo góc LMK bằng
A. 1200. B. 1400. C. 1450. D. 1600
Câu 5 Trong hình 3, biết sđ \(\widehat{BC}\)+sđ \(\widehat{ED}\)= 1700 thì số đo góc \(\widehat{CME}\) bằng
A. 1200. B. 1400. C. 1450. D. 950
Câu 6 Trong hình 3, biết sđ \(\widehat{EC}\)- sđ \(\widehat{BD}\)= 620 thì số đo góc  bằng
A. 200. B. 400. C. 310. D. 620
Câu 7 Trong hình 3, biết sđ \(\widehat{EC}\)- sđ \(\widehat{BD}\)= 620 thì số đo góc  bằng
A. 200. B. 400. C. 310. D. 620
Câu 8 Trong hình 3, biết sđ \(\widehat{EC}\)= 120 0; Â = 300 thì số đo cung BD bằng
A. 500. B. 600. C. 310. D. 620
-----------------------------------------
Với các dạng góc có đỉnh nằm bên trong và bên ngoài đường tròn, việc nắm vững lý thuyết kết hợp luyện tập bài tập có lời giải cụ thể sẽ giúp bạn giải toán chính xác và nhanh hơn. Hy vọng tài liệu này giúp bạn hiểu sâu kiến thức, làm bài vững vàng và đạt kết quả cao trong các kỳ thi Toán 9. Đừng quên lưu lại để ôn tập và chia sẻ cho bạn bè cùng học nhé!
