Phương trình bậc nhất hai ẩn Toán 9 – Lý thuyết, ví dụ và bài tập có đáp án chi tiết
Phương trình bậc nhất hai ẩn Toán 9
Trong chương trình Đại số Toán 9, phương trình bậc nhất hai ẩn là một chuyên đề nền tảng giúp học sinh rèn luyện kỹ năng giải toán và tư duy logic. Việc nắm vững lý thuyết và cách giải phương trình bậc nhất hai ẩn sẽ giúp bạn dễ dàng xử lý các bài toán thực tế, đồng thời hỗ trợ học tốt phần hệ phương trình bậc nhất hai ẩn ở các lớp sau.
Bài viết này tổng hợp lý thuyết, ví dụ minh họa, và bài tập có đáp án chi tiết, giúp bạn học nhanh – hiểu sâu – làm bài chính xác tuyệt đối. Cùng khám phá chuyên đề Đại số Toán 9 – Phương trình bậc nhất hai ẩn nhé!
A. Hình thành kiến thức
Bài toán đặt ra: Một hình chữ nhật có chiều dài là 
\(x\mathbf{\ }(cm)\) và chiều rộng \(y\mathbf{\ }(cm)\). Biết nửa chu vi của hình chữ nhật là \(16\mathbf{\ }cm\). Hãy lập hệ thức thể hiện mối quan hệ của ba đại lượng trên.
Hướng dẫn
Ta có hệ thức \(x + y = 16\)
Hệ thức \(x + y = 16\) là những ví dụ về phương trình bậc nhất hai ẩn.
Kết luận:
Phương trình bậc nhất hai ẩn \(x\) và \(y\) là hệ thức dạng: \(ax + by = c\) \((1)\)
Trong đó \(a,\mathbf{\ \ }b,\mathbf{\ \
}c\) là các số đã biết (\(a \neq
0\) hoặc \(b \neq 0\)).
Nếu \(x = x_{0}\) và \(y = y_{0}\), ta có \(ax_{0} + by_{0} = c\) là một khẳng định đúng thì cặp số \(\left( x_{0};\mathbf{\ \
}y_{0} \right)\) được gọi là một nghiệm của phương trình \((1)\).
B. Ví dụ minh họa về phương trình bậc nhất hai ẩn
Ví dụ 1: Trong các hệ thức sau, đâu là phương trình bậc nhất hai ẩn.
a) \(3x - 4y = 5\) b) \(0.\mathbf{\ }x + 0.\mathbf{\ }y =
3\) c) \(\frac{1}{3}x + \frac{\sqrt{2}}{4}y =
0\)
Hướng dẫn giải chi tiết
a) \(3x - 4y = 5\) là phương trình bậc nhất hai ẩn.
b) \(0.\mathbf{\ }x + 0.\mathbf{\ }y =
3\) không là phương trình bậc nhất hai ẩn vì hệ số cả \(x\) và \(y\) để bằng \(0\).
c) \(\frac{1}{3}x + \frac{\sqrt{2}}{4}y =
0\) là phương trình bậc nhất hai ẩn.
Ví dụ 2: Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau
a) \(- 2x + y = 4\) b) \(0x + y = 3\) c) \(- 2x + 0.\mathbf{\ }y =
4\)
Hướng dẫn giải chi tiết
a) Xét phương trình \(- 2x + y = 4\) \((1)\)
Ta viết phương trình \((1)\) thành \(y = 2x + 4\)
Như vậy mỗi cặp số \(\left( x;\mathbf{\ \
}y \right)\) hay \(\left( x;\mathbf{\ \
}2x + 4 \right)\) với mọi \(x\mathbb{\in R}\) đều là một nghiệm của phương trình \((1)\).
Khi đó ta nói rằng, phương trình \((1)\) có nghiệm tổng quát là \(\left( x;\mathbf{\ \ }2x + 4 \right)\) với mọi \(x\mathbb{\in R}\).
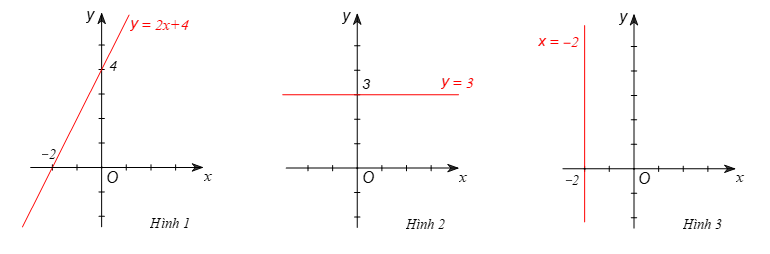
Tập hợp nghiệm của phương trình \((1)\) được biểu diễn bởi các điểm thuộc đường thẳng \(y = 2x +
4\) (Hình 1)
b) Xét phương trình \(0x + y = 3\) \((2)\)
Ta viết phương trình \((2)\) thành \(y = 3\).
Phương trình \((2)\) có nghiệm tổng quát là \(\left( x;\mathbf{\ \ }3
\right)\) với mọi \(x\mathbb{\in
R}\).
Tập hợp nghiệm của phương trình \((2)\) được biểu diễn bởi các điểm thuộc đường thẳng \(y = 3\) (Hình 2)
c) Xét phương trình \(- 2x + 0.\mathbf{\ }y
= 4\) \((3)\)
Ta viết phương trình \((3)\) thành \(- 2x = 4 \Rightarrow x = - 2\).
Phương trình \((3)\) có nghiệm tổng quát là \(\left( - 2;\mathbf{\ \ }y
\right)\) với mọi \(y\mathbb{\in
R}\).
Tập hợp nghiệm của phương trình \((3)\) được biểu diễn bởi các điểm thuộc đường thẳng \(x = - 2\) (Hình \(3\))
C. Bài tập vận dụng về phương trình bậc nhất hai ẩn
Bài tập 1: Trong các hệ thức sau, đâu là phương trình bậc nhất hai ẩn.
a) \(0.\mathbf{\ }x + 4y = 0\) b) \(\frac{3}{x} + \frac{1}{\sqrt{2}}y =
\frac{1}{4}\) c) \(2x^{2} - 4y = -
\frac{1}{5}\)
Bài tập 2: Cho phương trình bậc nhất hai ẩn \(2x - y = 3\).
a) Tính giá trị của \(y\) tương ứng trong bảng sau;
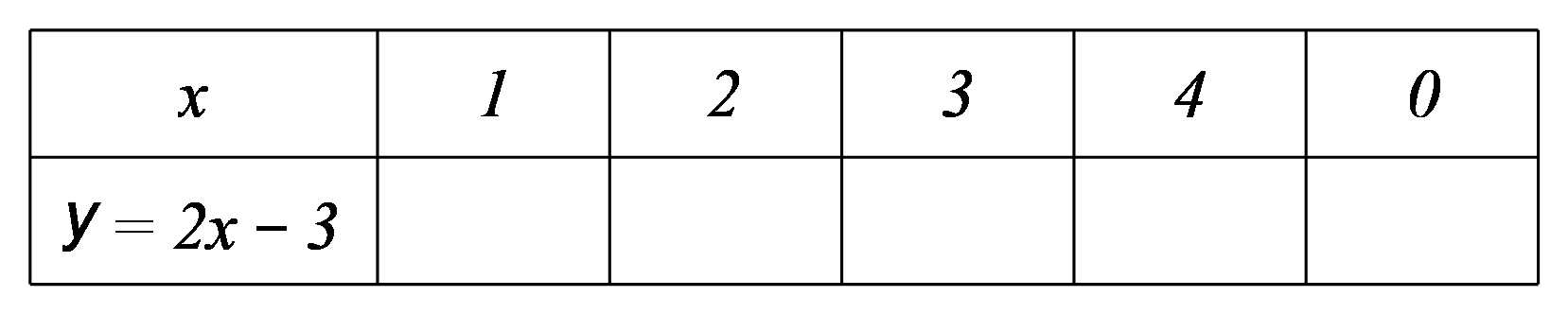
b) Viết nghiệm tổng quát của phương trình \(2x - y = 3\).
Bài tập 3: Cho phương trình bậc nhất hai ẩn \(- x + \frac{1}{3}y = 6\).
a) Trong các cặp số sau, cặp số nào là nghiệm của phương trình trên:
\(\left( 1;\mathbf{\ \ }3 \right),\mathbf{\
\ }\left( - 4;\mathbf{\ \ }6 \right),\mathbf{\ \ }\left( - 6;\mathbf{\ \
}0 \right)\) và \(\left( \frac{-
17}{3};\mathbf{\ \ }1 \right)\)
b) Viết nghiệm tổng quát của phương trình \(- x + \frac{1}{3}y = 6\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
---------------------------------
Qua bài viết trên, bạn đã nắm được kiến thức trọng tâm về phương trình bậc nhất hai ẩn trong Toán 9, bao gồm công thức, cách giải, ví dụ và bài tập có đáp án chi tiết. Hãy luyện tập thường xuyên để rèn tư duy logic và làm quen với dạng toán hệ phương trình bậc nhất hai ẩn – nền tảng quan trọng cho các chuyên đề Đại số nâng cao.
