Bài toán thực tế tam giác vuông – Hệ thức cạnh và góc có lời giải chi tiết

Trong chương trình Toán 9, các bài toán thực tế tam giác vuông thường gắn liền với kiến thức về hệ thức cạnh và góc. Đây là dạng toán quan trọng, không chỉ giúp học sinh củng cố kỹ năng vận dụng định lý Pythagore, các tỉ số lượng giác mà còn có ứng dụng rộng rãi trong thực tế như tính chiều cao, khoảng cách, độ dài… Bài viết này sẽ giới thiệu chi tiết phương pháp giải, kèm theo ví dụ minh họa có lời giải chi tiết, giúp các bạn học sinh lớp 9 rèn luyện tư duy logic, chuẩn bị vững vàng cho kỳ thi vào lớp 10 môn Toán.

A. Công thức hệ thức lượng trong tam giác vuông

Hình vẽ minh họa

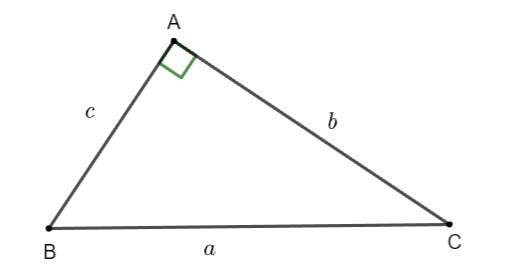
1. Hệ thức giữa cạnh huyền và cạnh góc vuông

2. Hệ thức giữa hai cạnh góc vuông

B. Bài tập thực tế minh họa áp dụng các hệ thức

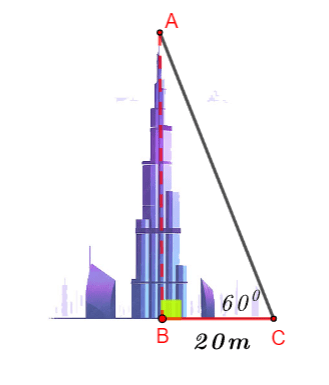
Hướng dẫn giải

Xét \(\Delta ABC\) vuông tại A có

\(\tan C = \frac{AB}{BC} \Rightarrow tan60^{\circ} = \frac{AB}{BC} \Rightarrow \sqrt{3} = \frac{AB}{20}\)

\(\Rightarrow AB = 20\sqrt{3}\ \approx 34,64\ \ \ (m)\)

Vậy chiều cao của tháp là \(34,64(m)\).

Hướng dẫn giải

a) Đường thẳng cắt trục tung tại 3630 nên \(b = 3630\).

\(\Rightarrow y = ax + 3630\ \ \ (d)\)

\((21;3000) \in (d):3000 = a.21 + 3630 \Leftrightarrow a = - 30\)

\(\Rightarrow\) Phương trình \((d):\ y = - 30\ x + 3630\)

b) Thế 2400 vào \(y\), ta có: \(2400 = - 30x + 3630 \Leftrightarrow x =41^0C\)

Vậy người thợ đó làm việc ở môi trường có nhiệt độ là 41°C.

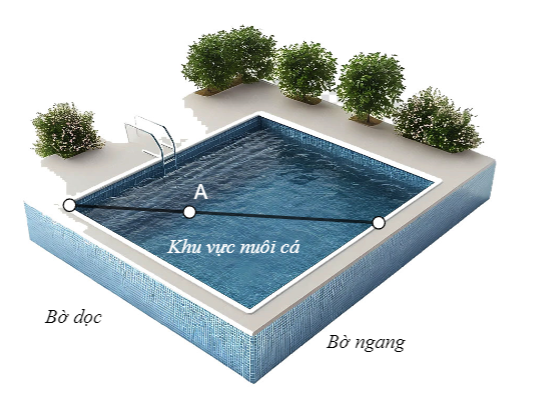
Hướng dẫn giải

Kí hiệu hình vẽ như sau :

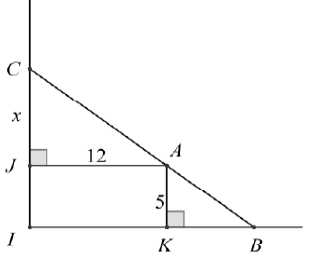
Đặt tên các điểm như hình vẽ. Đặt \(CJ = x,(x > 0).\)

Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên:

\(\frac{CJ}{AK} = \frac{JA}{KB}\Leftrightarrow \frac{x}{5}= \frac{12}{KB} \Leftrightarrow KB =\frac{60}{x}.\)

Diện tích của khu nuôi cá là:\(S = \frac{1}{2}(x + 5).\left( \frac{60}{x} + 12 \right).\)

\(\Leftrightarrow S(x) = \frac{1}{2}\left( 60 + 12x + \frac{300}{x} + 60 \right) \Leftrightarrow S(x) = 6x + \frac{150}{x} + 60\)

Áp dụng bất đẳng thức Cô si ta có:

\(6x + \frac{150}{x} \geq 2\sqrt{6x.\frac{150}{x}} = 60\)

Dấu bằng xảy ra khi \(6x = \frac{150}{x} \Leftrightarrow x^{2} = 25 \Leftrightarrow x = 5\).

Nên \(S(x) = 6x + \frac{150}{x} + 60 \geq 60 + 60 = 120\)

Suy ra diện tích nhỏ nhất có thể giăng là \(120(m^{2})\), đạt được khi \(x = 5\ m\).

Hướng dẫn giải

Tính chiều cao của cột cờ Hà Nội

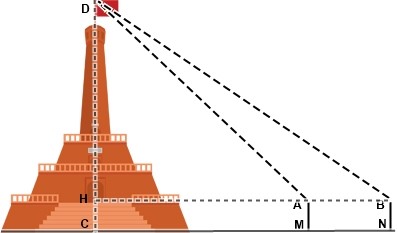
Gọi chiều cao của cột cờ là \(CD\) (m)

Theo đầu bài ta có: \(CH = AM = BN = 1\ m\); \(AB = 10\ m\); \(\widehat{DAH} = 50^{0}19'12''\)và \(\widehat{DBH} = 43^{0}16'\)

Xét \(\Delta AHD\) vuông tại \(H\), có

\(AH = DH.cot\widehat{DAH}\) (Hệ thức về cạnh và góc)

Xét \(\Delta BHD\) vuông tại \(H\), có

\(BH = DH.cot\widehat{DBH}\) (Hệ thức về cạnh và góc)

Mà \(AB = BH - AH\)\(\Rightarrow AB =DH.cot\widehat{DBH} - DH.cot\widehat{DAH}\)

\(\Leftrightarrow AB = DH.\left(\cot\widehat{DBH} - \cot\widehat{DAH} \right)\)\(\Leftrightarrow DH =\frac{AB}{\cot\widehat{DBH} - \cot\widehat{DAH}}\)

\(\Rightarrow DH = \frac{10}{cot43^{0}16' - cot50^{0}19'12''} \approx 42,96\)(m)

\(\Rightarrow CD = CH + HD \approx 1 + 42,96 = 43,96\) (m)

Vậy chiều cao của cột cờ Hà Nội xấp xỉ \(43,96\) m.

Hướng dẫn giải

Đưa bài toán về dữ kiện hình học: cho cây tre \(AB\) vuông góc mặt đất, đoạn tre \(BD\) bị gãy tại \(D\) và ngọn cây chạm đất tại \(C\); phần bị gãy \(CD\) tạo với mặt đất \(CA\) một góc 30 độ; người ta đo được \(AC\) bằng \(8,5\ m\). Tính chiều cao cây tre.

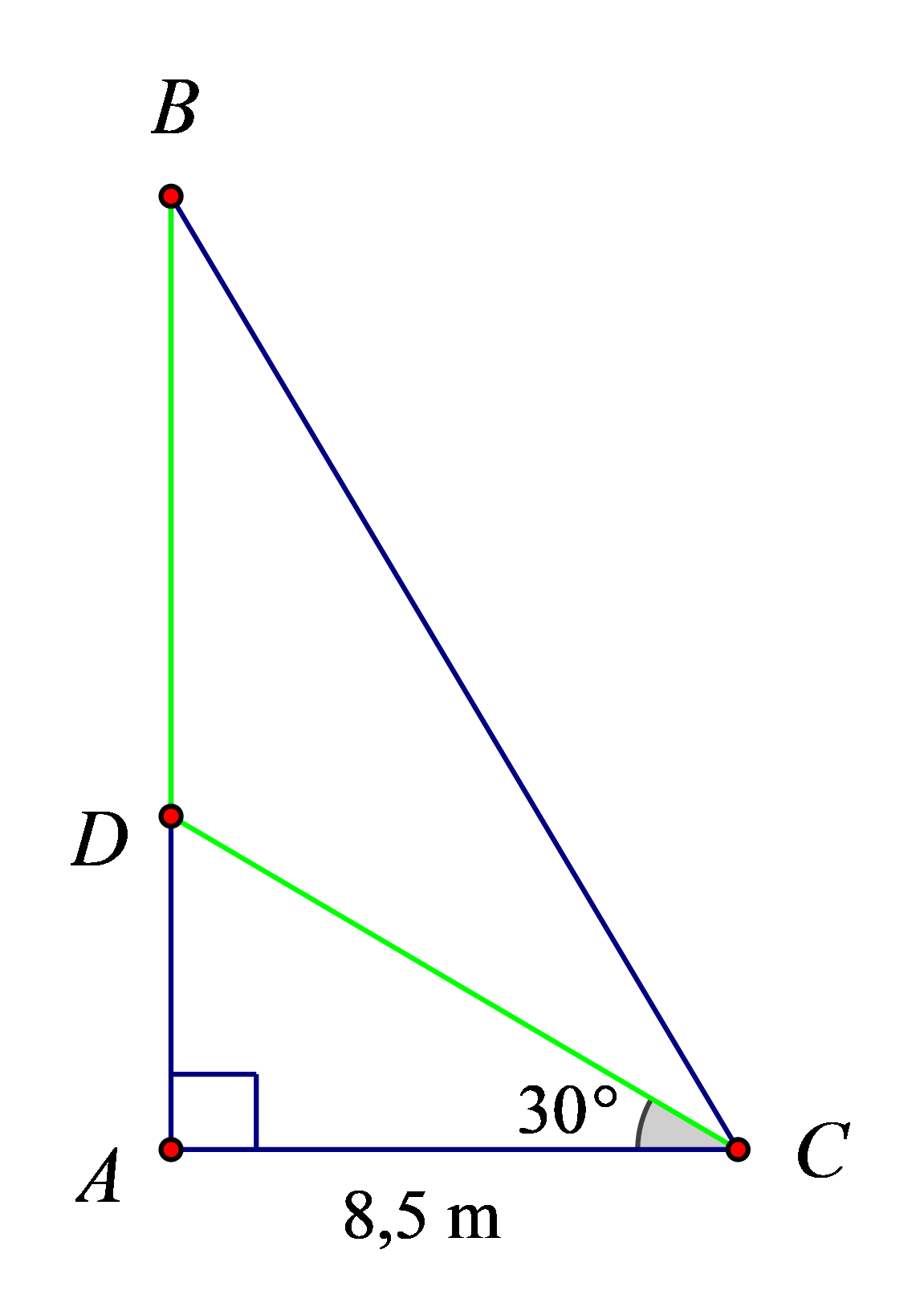
Tam giác \(ACD\) vuông tại \(A\) có \(AC = 8,5m;\ \widehat{ACD} = 30^{o}\)

Áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có:

\(AC = DC.cos\widehat{DCA}\)

\(\rightarrow CD =\frac{AC}{\cos\widehat{DCA}} = \dfrac{AC}{\cos30^{o}}\)\(=\dfrac{8,5}{\dfrac{\sqrt{3}}{2}} = \frac{17\sqrt{3}}{3}(m)\)

\(AD = AC.\tan\widehat{DCA} = 8,5.\tan30^{o}= \frac{17\sqrt{3}}{6}(m)\)

Suy ra \(AB = BD + AD = AD + CD\)

\(=\frac{17\sqrt{3}}{3} + \frac{17\sqrt{3}}{6} = \frac{17\sqrt{3}}{2}\approx 14,72\ (m)\)

Vậy cây tre cao \(14,72\ (m)\)

Bài tập 6. Một máy bay đang bay ở độ cao \(12\ km\). Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu cách sân bay \(320\ km\) máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?

b) Nếu phi công muốn tạo góc nghiêng \(5^0\) thì cách sân bay bao nhiêu kilômét phải bắt đầu cho máy bay hạ cánh (làm tròn đến chữ số thập phân thứ nhất)?

Hướng dẫn giải

a) Hình vẽ minh họa

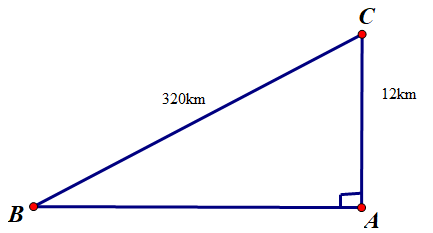
Xét \(\Delta ABC\) vuông tại \(A\), ta có:

\(\sin B = \frac{AC}{BC} = \frac{12}{320} = \frac{3}{80}\)

\(\Rightarrow \widehat{B} \approx 2^{{^\circ}}9'\)

Vậy góc nghiêng là \(2^{{^\circ}}9'\).

b) Hình vẽ minh họa

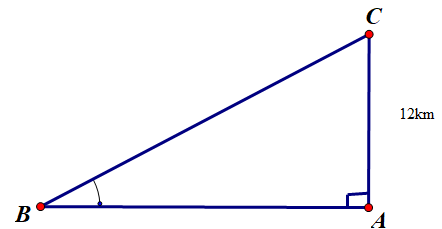
Xét \(\Delta ABC\) vuông tại \(A\), ta có:

\(sinB = \frac{AC}{BC}\)

\(\Rightarrow BC = \frac{AC}{sinB} = \frac{12}{\sin 5^{{^\circ}}} \approx 137,7\ km\).

Vậy phải bắt đầu cho máy bay hạ cánh khi máy bay cách sân bay \(137,7\ km\).

Bài tập 7. Hải đăng Kê Gà thuộc xã Tân Thành, huyện Hàm Thuận Nam, Bình Thuận là ngọn hải đăng được trung tâm sách kỷ luật Việt Nam xác nhận là ngọn hải đăng cao nhất và nhiều tuổi nhất. Hải đăng Kê Gà được xây dựng từ năm 1897-1899 và toàn bộ bằng đá. Tháp đèn có hình bát giác, cao \(66\ m\) so với mực nước biển. Ngọn đèn đặt trong tháp có thể phát sáng xa \(22\)hải lý (tương đương \(40\ km\)).

Một người đi thuyền thúng trên biển, muốn đến ngọn hải đăng có độ cao \(66\ m,\) người đó đứng trên mũi thuyền và dùng giác kế đo được góc giữa thuyền và tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là \(25{^\circ}.\) Tính khoảng cách của thuyền đến ngọn hải đăng (làm tròn đến \(m\)).

Hướng dẫn giải

Hình vẽ minh họa bài toán:

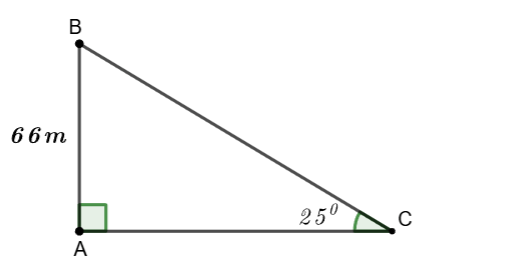
Xét \(\Delta ABC\) vuông tại \(A,\) ta có:

\(\tan C = \frac{AB}{AC}\)

\(\Rightarrow AC = \frac{AB}{\tan C} = \frac{66}{tan25{^\circ}} \approx 142\ (m)\)

Vậy khoảng cách của thuyền đến ngọn hải đăng là \(142\ m.\)

C. Bài tập vận dụng có đáp án chi tiết

Bài 1. Để do chiều cao của một ngọn tháp, không thể trèo lên đỉnh, người ta dùng thước dài, thước đo góc và đèn laser để thực hiện thao tác đó thu được kết quả như hình vẽ.

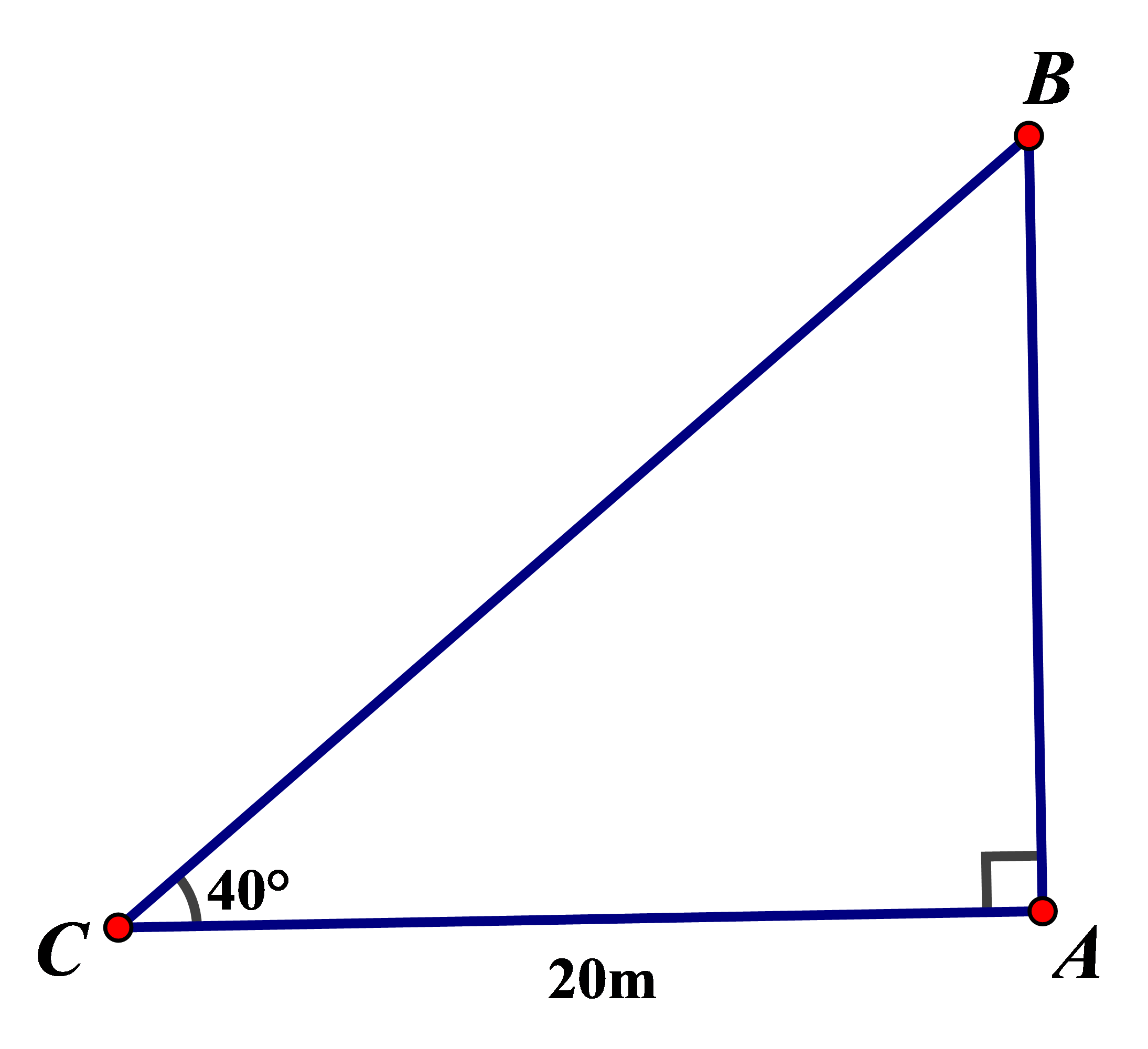
Hãy tính chiều cao của tháp.

Bài 2. Trong một buổi luyện tập, một tàu ngầm ở trên mặt biển bắt đầu lặn xuống và di

chuyển theo một đường thẳng tạo với mặt nước biển một góc \(21^{0}\). (Hình 30)

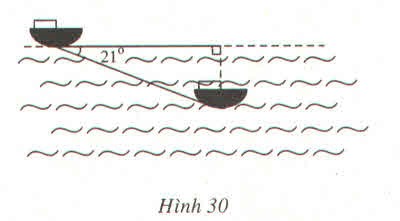
a) Khi tàu chuyển động theo hướng đó và đi được 250m thì tàu ở độ sâu bao nhiêu so với mặt nước (làm tròn đến hàng đơn vị).

b) Giả sử tốc độ trung bình của tàu là 9km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 mét (cách mặt nước biển 200m) (làm tròn đến phút).

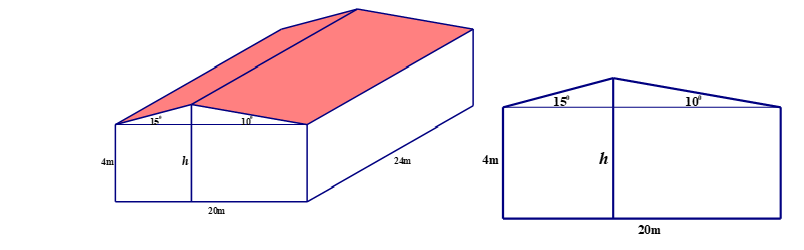
Bài 3. Một nhà xưởng với số liệu ghi trên hình (biết \(h\) là chiều cao từ mặt đất tới nóc nhà). Tính chiều cao \(h\) của nhà. Làm tròn kết quả đến chữ số thập phân thứ nhất.

Bài 4: Một khúc sông rộng khoảng \(250\ \ m\). Một chiếc đò chèo qua sông bị dòng nước đẩy lệch đi một góc \(40{^\circ}\). Hỏi con đò phải đi thêm bao nhiêu mét nữa so với dự định ban đầu để qua được khúc sông ấy?

Bài 5. Trên một khúc sông với hai bờ song song với nhau, có một chiếc đò dự định chèo qua sông từ vị trí \(A\) ở bờ bên này sang vị trí \(B\) ở bờ bên kia, đường thẳng \(AB\) vuông góc với các bờ sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cập bờ bên kia tại vị tri \(C\) cách \(B\) một khoảng bằng \(30\ \ m\). Biết khúc sông rộng \(150\ \ m\). Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây).

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

--------------------------------------------------------------

Qua việc luyện tập bài toán thực tế tam giác vuông – hệ thức cạnh và góc, học sinh không chỉ nắm chắc công thức lượng giác trong tam giác vuông mà còn:

• Thành thạo cách áp dụng vào các tình huống thực tế như đo độ cao, tính khoảng cách, xác định vị trí.

• Hiểu rõ mối liên hệ giữa toán học và đời sống, từ đó tăng hứng thú học tập.

• Rèn luyện kỹ năng trình bày logic, chặt chẽ và khoa học.

• Chuẩn bị nền tảng kiến thức quan trọng để bước vào chương trình hình học không gian ở bậc THPT.

👉 Việc giải quyết thành thạo dạng toán này sẽ giúp các em tự tin hơn trong đề kiểm tra, đề thi học kỳ và đặc biệt là kỳ thi tuyển sinh vào lớp 10. Hãy luyện tập thường xuyên, kết hợp học lý thuyết và bài tập thực tế để đạt kết quả cao nhất.