Các dạng bài toán Hình Trụ ôn thi vào 10 có lời giải chi tiết

Hình Trụ là một trong những dạng bài toán quan trọng trong chương trình Toán lớp 9, đặc biệt là khi ôn thi vào lớp 10. Việc hiểu rõ các dạng bài toán về hình trụ và luyện tập giải quyết các bài toán này sẽ giúp học sinh nắm vững kiến thức và tự tin trong kỳ thi sắp tới. Trong bài viết này, chúng tôi sẽ cung cấp cho bạn một cái nhìn tổng quan về các dạng bài toán hình trụ phổ biến, kèm theo lời giải chi tiết để bạn có thể luyện tập và cải thiện kỹ năng giải toán của mình. Cùng khám phá các bài toán hình trụ ôn thi vào 10 qua những ví dụ cụ thể và dễ hiểu!

A. Công thức tính hình trụ

Hình vẽ minh họa

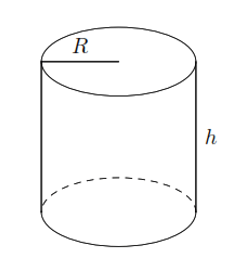
Công thức tính diện tích xung quanh hình trụ

\(S_{xq} = 2\pi Rh.\)

Công thức tính diện tích đáy hình trụ

\(S = \pi R^{2}.\)

Công thức tính diện tích toàn phần hình trụ

\(S_{tp} = 2\pi Rh + 2\pi R^{2}.\)

Công thức tính thể tích khối trụ

\(V = \pi R^{2}h.\)

B. Bài tập ví dụ minh họa Hình trụ có hướng dẫn chi tiết

Bài tập 1. Một xô nước inox hình trụ (không có nắp đậy) có chiều cao \(0,6\ m\), bán kính đáy \(0,2\ m\).

a) Tính diện tích inox để làm nên chiếc xô hình trụ trên (bỏ qua phần mép nối).

b) Trong xô có chứa nước, mực nước đó chiếm \(\frac{2}{3}\) chiều cao của xô. Tính thể tích nước có trong xô.

Hướng dẫn giải

a) Diện tích inox để làm nên chiếc xô hình trụ trên là:

S = S_{xung quanh} + S_đáy \(\approx 2.\pi.0,2.0,6 + 0,2^{2}.\pi = 0,28.\pi\left( m^{2} \right)\).

Vậy diện tích inox để làm nên chiếc xô hình trụ trên \(0,28\pi\ m^{2}\)

b) Thể tích nước có trong xô là

\(V = \pi.R^{2}.\frac{2}{3}h = \pi.0,2^{2}.\frac{2}{3}0,6 = 0,016.\pi(m^{3})\)

Bài tập 2: Một cái mũ bằng vải của nhà ảo thuật có dạng hình trụ và với kích thước mô phỏng như hình vẽ.

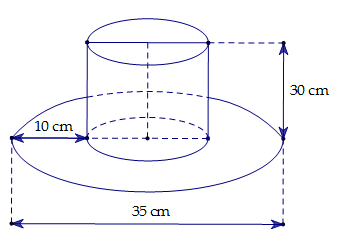
a) Hãy tính tổng diện tích vải cần có để làm nên cái mũ đó (không tính phần viền, mép dán) (làm tròn kết quả đến phần trăm).

b) Hãy tính thể tích phần có dạng hình nón của chiếc mũ đó (làm tròn kết quả đến phần trăm).

Hướng dẫn giải

a) Bán kính hình trụ của cái mũ là \(r = \frac{35 - 10 - 10}{2} = \frac{15}{2}\ \ (cm)\).

Đường cao hình trụ của cái mũ là \(30\ \ cm\).

Diện tích xung hình trụ là: \(S_{xq} = 2\pi rl = 2.\pi.\frac{15}{2}.30 = 450\pi\ \ \left( cm^{2} \right)\).

Diện tích vành mũ là: \(S_{v} = \pi\left( \frac{35}{2} \right)^{2} - \pi\left( \frac{15}{2} \right)^{2} = 250\pi\left( cm^{2} \right)\).

Vậy tổng diện tích vải cần có để làm nên cái mũ đó (không tính phần viền, mép dán) là: \(S = S_{xq} + S_{v} = 450\pi + 250\pi = 200\pi \approx \ \ 628,32\left( cm^{2} \right)\).

b) thể tích phần có dạng hình nón của chiếc mũ là

\(V = \pi r^{2}h = \pi\left( \frac{15}{2} \right)^{2}.30 = \frac{3375}{2}\pi \approx 5301,44\left( cm^{3} \right)\)

Bài tập 3: Một doanh nghiệp sản xuất vỏ hộp sữa ông thọ dạng hình trụ, có chiều cao bằng \(\mathbf{12}\mathbf{cm}\). Biết thể tích của hộp là \(192\pi cm^3\) Tính số tiền mà doanh nghiệp cần chi để sản xuất 10.000 vỏ hộp sữa ông thọ (kể cả hai nắp hộp), biết chi phí để sản xuất vỏ hộp đó là 80.000 đồng/m². (làm tròn kết quả đến hàng nghìn của \(m^2\)).

Hướng dẫn giải

Vì hộp sữa hình trụ có chiều cao h = 12cm và thể tích V_hộp =\(192\pi cm^3\) nên:

\(V = \pi r^{2}h\)

\(192\pi = 12\pi r^{2}\) suy ra \(r^{2} = 16\) suy ra \(r = 4cm\)

Vì hộp sữa hình trụ có r = 4cm  và chiều cao h = 12cm nên diện tích toàn phần của hộp sữa là:

\(S_{tp} = 2\pi r(h + r) \approx 402,124cm^{2} \approx 0,04m^{2}\)

Chi phí sản xuất 10.000 vỏ hộp sữa là : \(0,04.10000.80000=32000000\) đồng

Bài tập 4: Một cốc nước hình trụ có đường kính đáy là 10cm đang chứa nước nhưng chưa đầy. Người ta thả vào cốc 6 viên bi hình cầu giống hệt nhau thì thấy mực nước trong cốc dâng lên 5cm (và nước vẫn chưa đầy cốc). Tính bán kính của mỗi viên bi.

Hướng dẫn giải

Gọi \(R\) là bán kính viên bi. Thể tích \(6\) viên bi là thể tích nước dâng lên trong cốc. Khi đó thể tích \(6\) viên bi là \(V_{2} = 6.\frac{4}{3}\pi.R^{3} = 8\pi.R^{3}\)

Từ đó: \(8\pi.R^3 = 125\pi\Leftrightarrow R = \frac{5}{2}\) (cm)

C. Bài tập tự ôn tập có đáp án chi tiết

Bài tập 1: Một hộp đựng bóng tenis có dạng hình trụ. Biết rằng hộp chứa vừa khít ba quả bóng tenis được xếp theo chiều dọc, các quả bóng tenis có đường kính là \(6,2cm\) và có kích thức như nhau.

a) Tính thể tích hộp đựng bóng tenis.

b) Tính thể tích phần không gian còn trống bên trong là bao nhiêu? (Bỏ qua độ dày của vỏ hộp) (Lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ nhất).

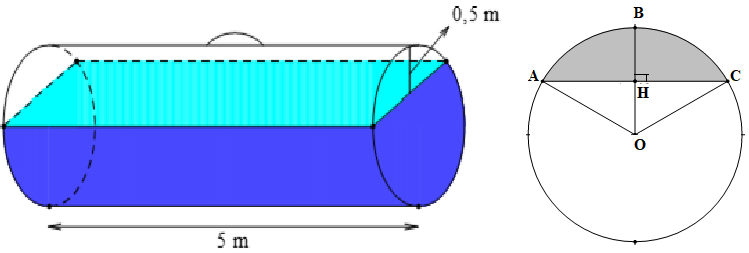
Bài tập 2: Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m, có bán kính đáy 1m, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn tương ứng với 0,5m của đường kính đáy. Tính thể tích gần dầu còn lại trong bồn (kết quả làm tròn 3 chữ số thập phân).

Bài tập 3: Gạch ống là một sản phẩm được tạo hình thành từ đất sét và nước, được kết hợp lại với nhau theo một công thức chung hợp lý mới có thể tạo ra hỗn hợp dẻo quánh, sau đó chúng được đổ vào khuôn, rồi đem phơi hoặc sấy khô và cuối cùng là đưa vào lò nung.

Một viên gạch hình hộp chữ nhật có kích thước dài \(20cm\), rộng \(8\ \ cm\). Bên trong có bốn lỗ hình trụ bằng nhau có đường kính \(2,5\ \ cm\).

a) Tính thể tích đất sét để làm một viên gạch. (lấy \(\pi = 3,14\))

b) Theo toán học, bác Ba muốn xây một ngôi nhà phải mua 10 thiên gạch, giá một viên là 1100 đồng.

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

------------------------------------------------

Việc làm quen và thực hành các dạng bài toán hình trụ sẽ giúp bạn làm chủ kiến thức và áp dụng vào bài thi vào lớp 10 một cách dễ dàng. Hy vọng bài viết này đã cung cấp cho bạn những phương pháp giải quyết bài toán hình trụ một cách rõ ràng và chi tiết. Đừng quên luyện tập thường xuyên để nâng cao kỹ năng và đạt kết quả cao trong kỳ thi vào 10. Chúc bạn học tốt và đạt thành tích xuất sắc trong kỳ thi sắp tới