Tìm vị trí điểm M trên đường tròn để biểu thức nhỏ nhất
Phương pháp giải bài toán cực trị hình học Toán 9
Trong chương trình Toán 9, chuyên đề tìm vị trí điểm M trên đường tròn để biểu thức nhỏ nhất là một dạng bài quen thuộc kết hợp giữa hình học và đại số. Dạng toán này giúp học sinh rèn luyện tư duy tối ưu hóa hình học, biết cách vận dụng định lý Pytago, hệ thức lượng trong đường tròn. Bài viết dưới đây sẽ hướng dẫn chi tiết cách xác định vị trí điểm M để biểu thức nhỏ nhất, kèm phân tích phương pháp giải, ví dụ minh họa và bài tập có đáp án, giúp bạn nắm chắc dạng toán đường tròn Toán 9 và tự tin trong các bài kiểm tra, đề thi vào lớp 10.
Bài tập 1. Cho nửa đường tròn 
\((O;R)\) đường kính \(AB\). Từ \(A\) và \(B\) vẽ hai tiếp tuyến \(Ax\) và \(By\). Một điểm \(M\) di động trên nửa đường tròn này qua \(M\) vẽ tiếp tuyến thứ ba cắt \(Ax\) và \(By\) lần lượt tại \(C\) và \(D\). Hãy xác định vị trí của điểm \(M\) trên nửa đường tròn \((O;R)\) sao cho \(AC + BD\) nhỏ nhất.
Hướng dẫn giải
Hình vẽ minh họa:
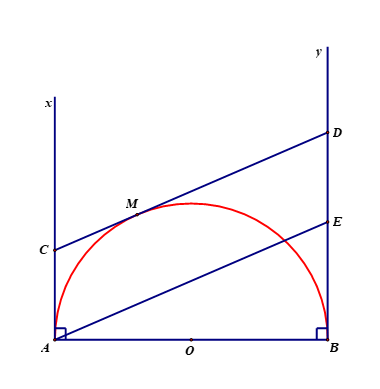
Kẻ \(AE//CD\) (E thuộc By)
Dễ thấy tứ giác ACDE là hình bình hành
\(\Rightarrow AE = CD\) mà \(AC = MC\) (tính chất 2 tiếp tuyến cắt nhau)
Tương tự \(BD = MD\) nên \(AC + BD = MC + MD = CD\)
Lại có \(AE \geq \ AB\)
\(\Leftrightarrow AC + BD \geq AB\) (không đổi)
Dấu “=” xảy ra \(\Leftrightarrow E \equiv
B\)
\(\Leftrightarrow CD//\ AB\) \(\Leftrightarrow OM\bot AB\).
Vậy khi \(M\) là giao điểm của đường thẳng vuông góc với AB thì \(AC + BD\) nhỏ nhất.
Bài tập 2. Cho nửa đường tròn \((O;R)\) đường kính \(AB\). Từ \(A\) và \(B\) vẽ hai tiếp tuyến \(Ax\) và \(By\). Một điểm \(M\) di động trên nửa đường tròn này qua \(M\) vẽ tiếp tuyến thứ ba cắt \(Ax\) và \(By\) lần lượt tại \(C\) và \(D\). Hãy xác định vị trí của điểm \(M\) trên nửa đường tròn \((O;R)\) sao cho \(3AC + BD\) nhỏ nhất.
Hướng dẫn giải
Hình vẽ minh họa:
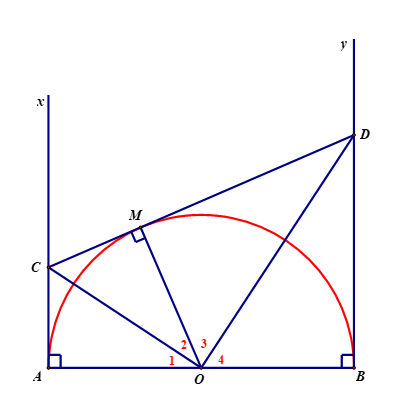
Ta có CM và CA là hai tiếp tuyến nên \(\widehat{O_{1}} = \widehat{O_{2}}\)
Tương tự \(\widehat{O_{3}} =
\widehat{O_{4}}\)
Mà \(\widehat{O_{1}} + \widehat{O_{2}} +
\widehat{O_{3}} + \widehat{O_{4}} = 180^{o}\)
\(\Rightarrow \widehat{O_{2}} +
\widehat{O_{3}} = 90^{o}\)
Hay tam giác COD vuông tại O
CD là tiếp tuyến tại M nên \(CD\bot
OM\)
Xét \(\Delta CMO\) và \(\Delta OMD\) có:
\(\widehat{CMO} = \widehat{DMO} =
90^{o}\), \(\widehat{O_{2}} =
\widehat{CDO}\) (cùng phụ với góc DCO)
Nên \(\Delta CMO\) \(\backsim \Delta OMD\) (g.g)
\(\Rightarrow \frac{CM}{OM} =
\frac{OM}{MD}\)
\(\Rightarrow CM.DM = OM^{2} =
R^{2}\) (không đổi)
Mà CM = AC, DM = BD \(\Rightarrow AC.BD =
R^{2}\)
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có: \(\frac{3AC + BD}{2} \geq
\sqrt{3.AC.BD}\)
\(\Leftrightarrow\) \(3AC + BD \geq 2\sqrt{3.AC.BD}
\Leftrightarrow\) \(3AC + BD \geq
2\sqrt{3}.R\)
Dấu “=” xảy ra \(\Leftrightarrow 3AC = BD =
\sqrt{3}.R\) \(\Leftrightarrow
\widehat{AOC} = 30^{0} \Leftrightarrow \widehat{AOM} =
60^{0}\)
Vậy M di động ở trên (O) sao cho \(\widehat{AOM} = 60^{o}\)thì \(3AC + BD\) nhỏ nhất.
Bài tập 3: Cho nửa đường tròn đường kính \(AB = 2R\). Từ A và B kẻ hai tiếp tuyến \(Ax, By\). Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến \(Ax, By\) lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N.
1. Chứng minh \(AC + BD = CD\). 2. Chứng minh \(\hat{COD } = 90^0\).
3. Chứng minh \(AC. BD =\) \(\frac{AB^{2}}{4}\). 4. Chứng minh \(OC // BM\).
5. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
6. Chứng minh \(MN ⊥ AB\).
7. Xác định vị trí của M để chu vi tứ giác ACDB đạt giá trị nhỏ nhất.
Hướng dẫn giải
Hình vẽ minh họa:
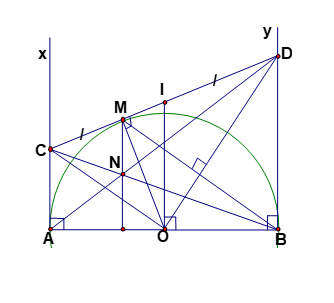
1. Theo tính chất hai tiếp tuyến cắt nhau ta có: \(CA = CM; DB = DM\)
\(=> AC + BD = CM + DM\).
Mà \(CM + DM = CD => AC + BD = CD\)
2. Theo tính chất hai tiếp tuyến cắt nhau ta có: OC là tia phân giác của góc AOM; OD là tia phân giác của góc BOM, mà ∠AOM và ∠BOM là hai góc kề bù => \(\hat{COD } = 90^0\).
3. Theo trên \(\hat{COD } = 90^0\) nên tam giác COD vuông tại O có OM ⊥ CD ( OM là tiếp tuyến ).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có OM2 = CM. DM.
Mà \(OM = R; CA = CM; DB = DM\) \(=> AC. BD =R^2\) => AC. BD = \(\frac{AB^{2}}{4}\).
4. Theo trên \(\hat{COD } = 90^0\) nên \(OC ⊥ OD\).(1)
Theo tính chất hai tiếp tuyến cắt nhau ta có: ; lại có \(OM = OB =R\) => OD là trung trực của BM => \(BM ⊥ OD\).(2).
Từ (1) và (2) \(=> OC // BM\) ( Vì cùng vuông góc với OD).
5. Gọi I là trung điểm của CD ta có I là tâm đường tròn ngoại tiếp tam giác COD đường kính CD có IO là bán kính.
Theo tính chất tiếp tuyến ta có \(AC ⊥ AB; BD ⊥ AB\) \(=> AC // BD\)
=> Tứ giác ACDB là hình thang. Lại có I là trung điểm của CD; O là trung điểm của AB => IO là đường trung bình của hình thang ACDB
\(\Rightarrow\) IO // AC , mà \(AC ⊥ AB => IO ⊥ AB\) tại O => AB là tiếp tuyến tại O của đường tròn đường kính CD
6. Theo trên \(AC // BD\) => \(\frac{CN}{BN}\ = \ \frac{AC}{BD}\), mà \(CA = CM; DB = DM\) nên suy ra \(\frac{CN}{BN}\ = \
\frac{CM}{DM}\)
\(=> MN // BD\) mà \(BD ⊥ AB => MN ⊥ AB\).
7. Ta có chu vi tứ giác ACDB bằng \(AB + AC + CD + BD\) mà \(AC + BD = CD\) nên suy ra chu vi tứ giác ACDB bằng \(AB + 2CD\) mà AB không đổi nên chu vi tứ giác ACDB nhỏ nhất khi CD nhỏ nhất , mà CD nhỏ nhất khi CD là khoảng cách giữ Ax và By tức là CD vuông góc với Ax và By. Khi đó CD // AB => M phải là trung điểm của cung AB.
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu
--------------------------------------------
Qua bài viết tìm vị trí điểm M trên đường tròn để biểu thức nhỏ nhất, bạn đã nắm được phương pháp phân tích, lập luận hình học và cách xử lý biểu thức hiệu quả. Hãy luyện thêm các bài tập mở rộng về cực trị hình học, quỹ tích điểm và tiếp tuyến của đường tròn để nâng cao kỹ năng giải nhanh và chính xác.
