Ứng dụng thực tế tỉ số lượng giác của góc nhọn

Trong chương trình Toán 9, chuyên đề hệ thức lượng trong tam giác vuông là một phần kiến thức quan trọng, gắn liền với các tỉ số lượng giác của góc nhọn. Không chỉ dừng lại ở lý thuyết và bài tập trên lớp, các công thức lượng giác còn có rất nhiều ứng dụng thực tế như tính chiều cao tòa nhà, độ dài bóng cây, khoảng cách giữa hai điểm hay góc nghiêng trong kỹ thuật. Bài viết này sẽ giúp học sinh hiểu rõ hơn về bản chất của tỉ số lượng giác, đồng thời vận dụng linh hoạt kiến thức để giải quyết các tình huống thực tiễn, từ đó học tập hiệu quả hơn và có hứng thú với môn Toán.

A. Bài tập ví dụ minh họa ứng dụng thực tế tỉ số lượng giác của góc nhọn

Hướng dẫn giải

Hình vẽ minh họa

Ta có chiều cao cột đèn là \(AC;AB = 6\ m\) và \(\widehat{ACB} = 38{^\circ}\)

Xét tam giác \(ACB\) vuông tại \(A\) có:

\(AC = AB.tanB = 7,5.tan38{^\circ} \simeq 4,69m\).

Vậy cột đèn cao \(4,69\ m\).

Hướng dẫn giải

Hình vẽ minh họa

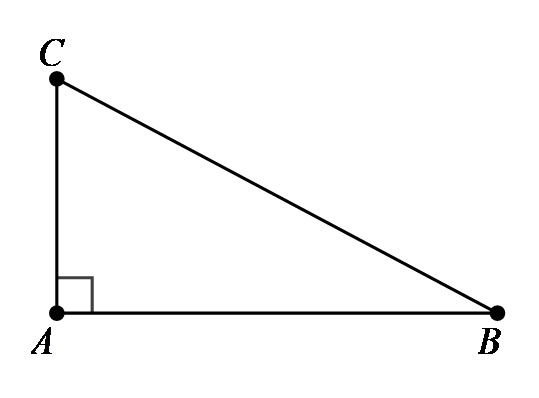
Đổi \(1,2' = \frac{1}{50}h\).

Sau \(1,2\) phút máy bay ở \(C\).

Quãng đường bay được là \(BC = 500.\frac{1}{50} = 10\ km\) và \(\widehat{B} = 30{^\circ}\)

Nên \(AC = BC.sin30{^\circ} = 5\ km\).

Vậy máy bay đạt được độ cao là \(5\ km\) sau \(1,2\) phút.

Hướng dẫn giải

Hình vẽ minh họa

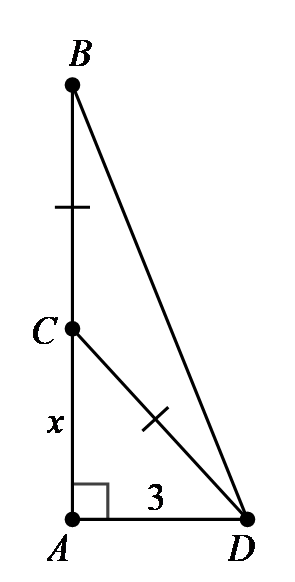
Giả sử \(AB\) là độ cao của cây tre, \(C\) là điểm gãy.

Đặt \(AC = x\ (0 < x < 9) \Rightarrow CB = CD = 9 - x\).

Vì \(\Delta ACD\) vuông tại \(A\).

Suy ra \(AC^{2} + AD^{2} = CD^{2}\)

\(\Leftrightarrow x^{2} + 3^{2} = (9 - x)^{2}\)

\(\Leftrightarrow x = 4\) thoả mãn.

Vậy điểm gãy cách gốc cây \(4\ m\).

B. Bài tập tự rèn luyện có hướng dẫn giải chi tiết

Bài tập 1: Hai bạn học sinh Trung và Dũng đang đứng ở mặt đất bằng phẳng, cách nhau \(100m\) thì nhìn thấy một chiếc diều (ở vị trí \(C\) giữa hai bạn). Biết góc “nâng” để nhìn thấy diều ở vị trí của Trung là \(50{^\circ}\) và góc “nâng” để nhìn thấy diều ở vị trí của Dũng là \(40{^\circ}\). Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai).

Bài tập 2: Một cầu trượt trong công viên có độ dốc là \(28{^\circ}\) và có độ cao là \(2,1\ m\). Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).

Bài tập 3: Một cột đèn điện \(AB\) cao \(7m\) có bóng in trên mặt đất là \(AC\) dài \(4m\). Hãy tính góc \(\widehat{BCA}\) (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.

Bài tập 4: Một cây tre cao \(8\ m\) bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc \(3,5\ m\). Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai) ?

Bài tập 5: Hai bạn học sinh \(A\) và \(B\) đang đứng ở mặt đất bằng phẳng, cách nhau \(80\ m\) thì nhìn thấy một máy bay trực thẳng điều khiển từ xa (ở trị ví \(C\) nằm trên tia \(AB\) và \(AC > AB\)). Biết góc “nâng” để nhìn thấy máy bay ở vị trí của \(B\) là \(55{^\circ}\) góc “nâng” để nhìn thấy máy bay ở vị trí của \(B\) là \(40{^\circ}\). Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai).

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

--------------------------------------------------------------

Có thể khẳng định rằng, việc nắm vững và biết cách ứng dụng tỉ số lượng giác của góc nhọn không chỉ giúp học sinh học tốt chuyên đề hệ thức lượng trong tam giác vuông, mà còn mở rộng khả năng tư duy và gắn kết kiến thức với đời sống. Qua đó, học sinh sẽ thấy rằng Toán học không hề khô khan mà rất gần gũi và hữu ích trong nhiều lĩnh vực: từ đo đạc, xây dựng, kiến trúc, cho đến khoa học tự nhiên và công nghệ.

Để đạt kết quả cao, các em nên thường xuyên luyện tập dạng bài toán thực tế, kết hợp cùng việc ghi nhớ công thức cơ bản và rèn kỹ năng phân tích tình huống. Nhờ đó, kiến thức sẽ trở nên vững chắc hơn, giúp học sinh tự tin chinh phục các kỳ thi quan trọng, đặc biệt là kỳ thi tuyển sinh vào lớp 10.