Hệ phương trình bậc nhất hai ẩn – Định nghĩa và ví dụ minh họa dễ hiểu
Hệ phương trình Toán 9
Trong chương trình Toán 9, hệ phương trình bậc nhất hai ẩn là một phần kiến thức trọng tâm của chuyên đề Đại số. Đây là dạng toán thường xuyên xuất hiện trong đề kiểm tra và đề thi vào 10, đòi hỏi học sinh hiểu rõ khái niệm, cách giải và ứng dụng thực tế. Bài viết này sẽ giúp bạn nắm vững định nghĩa, dạng tổng quát và ví dụ minh họa dễ hiểu về hệ phương trình bậc nhất hai ẩn, kèm bài tập có đáp án chi tiết. Cùng khám phá ngay để học tốt chuyên đề Toán 9 có đáp án nhé!
A. Định nghĩa hệ phương trình bậc nhất hai ẩn
Mỗi cặp gồm hai phương trình bậc nhất hai ẩn 
\(\left\{ \begin{matrix}
ax + by = c \\
a'x + b'y = c'
\end{matrix} \right.\ (1)\) được gọi là một hệ phương trình bậc nhất hai ẩn.
Mỗi cặp số \(\left( x_{0};\ \ y_{0}
\right)\) được gọi là một nghiệm của hệ \((1)\) nếu nó đồng thời là nghiệm của hai phương trình của hệ \((1)\).
Ví dụ: Cho hệ phương trình \(\left\{
\begin{matrix}
2x - y = 0 \\
x + y = 3
\end{matrix} \right.\).
Nhận thấy cặp số \((1;\ \ 2)\) vừa là nghiệm của phương trình
\(2x - y = 0\) vừa là nghiệm của phương trình \(x + y = 3\) nên cặp \((1;\ \ 2)\) là nghiệm của phương trình trên.
Biểu diễn tập nghiệm của hệ phương trình trên mặt phẳng tọa độ như hình vẽ.
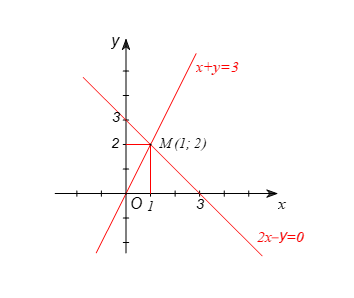
Ví dụ: Trong các cặp số \((1;\ \ - 3),\ \
( - 1;\ \ 3)\) cặp nào là nghiệm của hệ phương trình \(\left\{ \begin{matrix}
4x - y = 7 \\
5x + y = 2
\end{matrix} \right.\).
Hướng dẫn giải
Thay cặp số \((1;\ \ - 3)\) vào hệ phương trình ta được \(\left\{ \begin{matrix}
4.\ 1 - ( - 3) = 7 \\
5.\ 1 + ( - 3) = 2
\end{matrix} \right.\) (thỏa mãn)
Nên \((1;\ \ - 3)\) là nghiệm của hệ phương trình.
Thay cặp số \(( - 1;\ \ 3)\) vào hệ phương trình, ta được \(\left\{ \begin{matrix}
4.\ ( - 1) - 3 = 7 \\
5.\ ( - 1) + 3 = 2
\end{matrix} \right.\) (vô lý)
Nên \(( - 1;\ \ 3)\) không phải là nghiệm của hệ phương trình.
B. Bài tập vận dụng có hướng dẫn chi tiết
Bài 1: Cho hệ phương trình \(\left\{
\begin{matrix}
3x + y = 3 \\
2x - y = 7
\end{matrix} \right.\). Cặp số nào sau đây là nghiệm của hệ phương trình trên
a) \((5;\ \ 1)\) b) \((1;\ \ - 5)\) c) \((2;\ \ - 3)\)
Bài 2: Cho hệ phương trình sau \(\left\{
\begin{matrix}
y = 3 \\
2x + y = 1
\end{matrix} \right.\). Hãy tìm nghiệm của hệ phương trình trên.
Bài 3: Cho hệ phương trình \(\left\{
\begin{matrix}
x = - 2 \\
- x + 3y = 1
\end{matrix} \right.\). Hãy tìm nghiệm của hệ phương trình trên.
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
------------------------------------------------
Trên đây là toàn bộ kiến thức cơ bản về hệ phương trình bậc nhất hai ẩn trong Toán 9, bao gồm định nghĩa, dạng tổng quát và ví dụ minh họa dễ hiểu. Hy vọng bài viết giúp bạn hiểu rõ bản chất, rèn luyện kỹ năng giải nhanh và chính xác các dạng bài tập liên quan.
