Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc của tam giác vuông

Hệ thức lượng trong tam giác vuông

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách tính cạnh và góc tam giác vuông

A. Công thức tỉ số lượng giác của góc nhọn
- Định lý Pythagore cho tam giác vuông
B. Bài tập tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc của tam giác
C. Bài tập tự rèn luyện có hướng dẫn đáp án

Trong chương trình Toán 9, chuyên đề hệ thức lượng trong tam giác vuông giữ vai trò quan trọng, giúp học sinh hiểu rõ mối liên hệ giữa cạnh và góc, từ đó vận dụng vào nhiều dạng bài tập. Việc tính tỉ số lượng giác của góc nhọn, hay tìm cạnh và góc của tam giác vuông, không chỉ củng cố kiến thức lượng giác cơ bản mà còn là kỹ năng cần thiết trong các kỳ kiểm tra và ôn thi vào lớp 10. Bài viết này sẽ cung cấp hệ thống kiến thức, ví dụ minh họa và hướng dẫn giải chi tiết, giúp học sinh học nhanh – hiểu sâu – vận dụng hiệu quả.

A. Công thức tỉ số lượng giác của góc nhọn

Với $\alpha$ $\alpha$ là góc nhọn trong tam giác vuông ta có:

$\sin\alpha = \frac{canh\ doi}{canh\ huyen}$ $\sin\alpha = \frac{canh\ doi}{canh\ huyen}$; $\cos\alpha = \frac{canh\ ke\ }{canh\ huyen}$ $\cos\alpha = \frac{canh\ ke\ }{canh\ huyen}$;

$\tan\alpha = \frac{canh\ doi}{canh\ ke}$ $\tan\alpha = \frac{canh\ doi}{canh\ ke}$; $\cot\alpha = \frac{canh\ ke}{canh\ doi\ }$ $\cot\alpha = \frac{canh\ ke}{canh\ doi\ }$.

$\tan\alpha = \frac{\sin\alpha}{\cos\alpha}$ $\tan\alpha = \frac{\sin\alpha}{\cos\alpha}$; $\cot\alpha = \frac{\cos\alpha}{\sin\alpha}$ $\cot\alpha = \frac{\cos\alpha}{\sin\alpha}$; $\tan\alpha.cot\alpha = 1$ $\tan\alpha.cot\alpha = 1$;

Định lý Pythagore cho tam giác vuông

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

B. Bài tập tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc của tam giác

Ví dụ 1: Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,BC = 13cm$.

a) Tính tỉ số lượng giác của góc $\widehat{ACB}$ $\widehat{ACB}$.

b) Vẽ hai tia phân giác $BE,CF$ cắt nhau tại $I$.Tính $AE,EC,AF, BF$.

Hướng dẫn giải

Hình vẽ minh họa

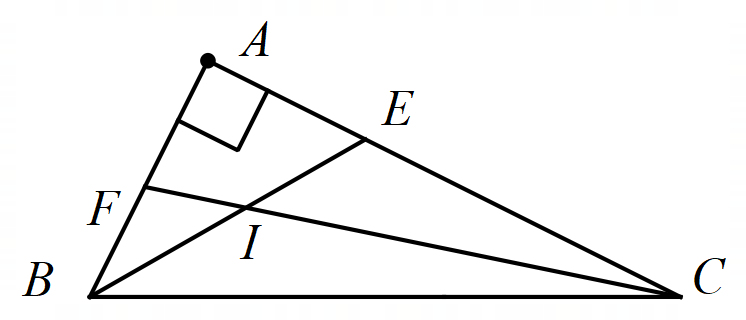
a. Xét $\Delta ABC$ $\Delta ABC$ vuông tại $A$ có:

$AC = \sqrt{BC^{2} - BA^{2}} = \sqrt{13^{2} - 5^{2}} = 12cm$ $AC = \sqrt{BC^{2} - BA^{2}} = \sqrt{13^{2} - 5^{2}} = 12cm$

Trong $\Delta ABC$ $\Delta ABC$ vuông tại $A$ có:

$\sin\widehat{ACB} = \frac{AB}{BC} = \frac{5}{13}$ $\sin\widehat{ACB} = \frac{AB}{BC} = \frac{5}{13}$; $\cos\widehat{ACB} = \frac{AC}{BC} = \frac{12}{13}$ $\cos\widehat{ACB} = \frac{AC}{BC} = \frac{12}{13}$

$\tan\widehat{ACB} = \frac{\sin\widehat{ACB}}{\cos\widehat{ACB}} = \frac{5}{12}$ $\tan\widehat{ACB} = \frac{\sin\widehat{ACB}}{\cos\widehat{ACB}} = \frac{5}{12}$; $\cot\widehat{ACB} = \frac{1}{\tan\widehat{ACB}} = \frac{12}{5}$ $\cot\widehat{ACB} = \frac{1}{\tan\widehat{ACB}} = \frac{12}{5}$.

b) Áp dụng tính chất đường phân giác trong $\Delta ABC$ $\Delta ABC$ ta có:

$\frac{AB}{AE} = \frac{BC}{CE} \Rightarrow \frac{AE}{5} = \frac{CE}{13} = \frac{AE + CE}{5 + 13} = \frac{AC}{18} = \frac{2}{3}$ $\frac{AB}{AE} = \frac{BC}{CE} \Rightarrow \frac{AE}{5} = \frac{CE}{13} = \frac{AE + CE}{5 + 13} = \frac{AC}{18} = \frac{2}{3}$

Vậy $AE = \frac{10}{3}cm.CE = \frac{26}{3}cm.$ $AE = \frac{10}{3}cm.CE = \frac{26}{3}cm.$

$\frac{AC}{AF} = \frac{CB}{BF} \Rightarrow \frac{AF}{12} = \frac{BF}{13} = \frac{AF + BF}{12 + 13} = \frac{AC}{25} = \frac{1}{5}$ $\frac{AC}{AF} = \frac{CB}{BF} \Rightarrow \frac{AF}{12} = \frac{BF}{13} = \frac{AF + BF}{12 + 13} = \frac{AC}{25} = \frac{1}{5}$

Vậy $AF = \frac{12}{5}cm;BF = \frac{13}{5}cm$ $AF = \frac{12}{5}cm;BF = \frac{13}{5}cm$.

Ví dụ 2: Cho hình vuông $ABCD$ có $AD = \ 12cm$ $AD = \ 12cm$, điểm $M$ trên $BC$, điểm $N$ trên $AB$sao cho$AN = BM = 5cm$.

a) Tính tỉ số lượng giác của góc $\widehat{AMB}$ $\widehat{AMB}$

b) Nối $DN$ cắt$AM$ tại$K$. Chứng minh$AM = DN$.

c) Chứng minh $AM\bot DN$ $AM\bot DN$.

Hướng dẫn giải

Hình vẽ minh họa

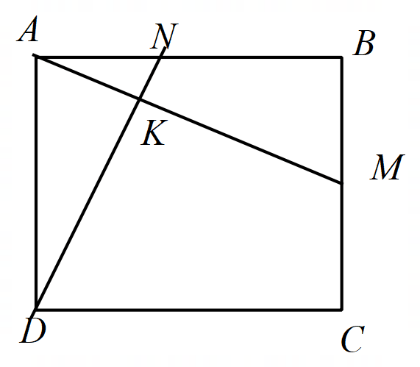
a) Xét $\Delta AMB$ $\Delta AMB$ vuông tại $B$có: $AM = \sqrt{BA^{2} - BM^{2}} = \sqrt{5^{2} + 12^{2}} = 13cm$ $AM = \sqrt{BA^{2} - BM^{2}} = \sqrt{5^{2} + 12^{2}} = 13cm$

Ta có:

$\sin\widehat{AMB} = \frac{AB}{AM} = \frac{12}{13}$ $\sin\widehat{AMB} = \frac{AB}{AM} = \frac{12}{13}$; $cos\widehat{AMB} = \frac{BM}{AM} = \frac{5}{13}$ $cos\widehat{AMB} = \frac{BM}{AM} = \frac{5}{13}$;

$\tan\widehat{AMB} =\frac{AB}{BM} =\frac{12}{5}$ $\tan\widehat{AMB} =\frac{AB}{BM} =\frac{12}{5}$; $\cot\widehat{AMB} = \frac{1}{\tan\widehat{AMB}} = \frac{5}{12}$ $\cot\widehat{AMB} = \frac{1}{\tan\widehat{AMB}} = \frac{5}{12}$.

b) Xét $\Delta AMB = \Delta DNA(c.g.c) \Rightarrow AM = DN$ $\Delta AMB = \Delta DNA(c.g.c) \Rightarrow AM = DN$.

c) Ta có: $\tan\widehat{BAM} = \frac{BM}{AB}$ $\tan\widehat{BAM} = \frac{BM}{AB}$; $\cot\widehat{AND} = \frac{AN}{AD}$ $\cot\widehat{AND} = \frac{AN}{AD}$.

Do $BM = AN;AB = AD$

$\Rightarrow \tan\widehat{BAM} = \cot\widehat{AND}$ $\Rightarrow \tan\widehat{BAM} = \cot\widehat{AND}$ nên trong $\Delta AKN$ $\Delta AKN$ có: $\widehat{BAM}$ $\widehat{BAM}$ và $\widehat{AND}$ $\widehat{AND}$ phụ nhau.

Suy ra $\widehat{AKN} =90^0$ $\widehat{AKN} =90^0$.

Vậy $AM\bot DN$ $AM\bot DN$.

Ví dụ 3. Cho $\Delta ABC$ $\Delta ABC$, đường cao $BM$ và $CN$ cắt nhau tại $H$.

a) Biết $MA = 6cm$,$AB = 10cm$. Tính tỉ số lượng giác của $\widehat{A}$ $\widehat{A}$.

b) Chứng tỏ rằng $\widehat{ABM} = \widehat{ACN}$ $\widehat{ABM} = \widehat{ACN}$; $AH\bot BC$ $AH\bot BC$.

c) Gọi $I,J$ lần lượt là trung điểm của $AH,\ BC$ $AH,\ BC$. Chứng tỏ rằng: $IJ\bot MN$ $IJ\bot MN$

Hướng dẫn giải

a) Ta có: $\sin\widehat{MAB} = \frac{4}{5}$ $\sin\widehat{MAB} = \frac{4}{5}$; $\cos\widehat{MAB} = \frac{3}{5}$ $\cos\widehat{MAB} = \frac{3}{5}$; $\tan\widehat{MAB} = \frac{4}{3}$ $\tan\widehat{MAB} = \frac{4}{3}$; $\cot\widehat{MAB} = \frac{3}{4}$ $\cot\widehat{MAB} = \frac{3}{4}$

b) Ta có : $\widehat{ABM} = \widehat{ACN}$ $\widehat{ABM} = \widehat{ACN}$( cùng phụ với $\widehat{BAC}$ $\widehat{BAC}$)

Chứng tỏ $H$ là trực tâm của $\Delta ABC$ $\Delta ABC$. Nên $AH\bot BC$ $AH\bot BC$.

c) Ta chứng minh : $MI = NI = \frac{AH}{2}$ $MI = NI = \frac{AH}{2}$ và $MJ = NJ = \frac{BC}{2}$ $MJ = NJ = \frac{BC}{2}$ nên $I,J$ thuộc trung trực của $MN$. Vậy $IJ\bot MN$ $IJ\bot MN$.

C. Bài tập tự rèn luyện có hướng dẫn đáp án

Bài tập 1: Cho $\alpha$ $\alpha$ là một góc nhọn. Hãy giải thích:

a) $sin\ \alpha < \ tan\ \ \alpha;$ $sin\ \alpha < \ tan\ \ \alpha;$ b) $cos\ \ \alpha < \ \cot\ \alpha$ $cos\ \ \alpha < \ \cot\ \alpha$ .

Bài tập 2: Cho tam giác vuông tại A, trong đó AC = 0,9m; AB = 1,2 m. Tính các tỉ số lượng giác của góc B, từ đó suy ra tỉ số lượng giác của góc C.

Bài tập 3. Cho tam giác ABC vuông tại A, đường cao AH. Tính $\sin B,\ \ \sin C$ $\sin B,\ \ \sin C$ biết rằng:

a) AB = 13 và BH = 5; b) BH = 3 và CH = 4.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

----------------------------------------------------------------------

FAQ – Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc của tam giác vuông

1. Tỉ số lượng giác của góc nhọn là gì?

Tỉ số lượng giác của góc nhọn là các tỉ số giữa độ dài các cạnh trong tam giác vuông, bao gồm sin, cos, tan (tg) và cot (cotg) . Đây là kiến thức trọng tâm của chương Hệ thức lượng trong tam giác vuông và được sử dụng để tính cạnh, tính góc cũng như giải nhiều bài toán thực tế.

2. Muốn tính tỉ số lượng giác của một góc nhọn cần biết những gì?

Để tính được tỉ số lượng giác, học sinh cần xác định đúng:

Cạnh huyền.
Cạnh đối với góc đang xét.
Cạnh kề với góc đang xét.

Sau đó áp dụng đúng công thức của sin, cos, tan hoặc cot để tìm kết quả.

3. Làm thế nào để tính cạnh của tam giác vuông bằng tỉ số lượng giác?

Khi biết một góc nhọn và một cạnh của tam giác vuông, học sinh có thể sử dụng các công thức lượng giác để tính cạnh còn lại. Việc lựa chọn sin, cos hay tan phụ thuộc vào dữ kiện của bài toán và cạnh cần tìm.

4. Cách tính góc của tam giác vuông như thế nào?

Nếu biết hai cạnh hoặc biết một tỉ số lượng giác, học sinh sử dụng máy tính cầm tay hoặc bảng giá trị lượng giác để tìm số đo góc. Sau khi xác định một góc nhọn, góc còn lại được tính bằng tổng hai góc nhọn bằng 90° .

5. Những dạng bài tập thường gặp về tỉ số lượng giác lớp 9 là gì?

Các dạng bài phổ biến gồm:

Tính sin, cos, tan, cot của góc nhọn.
Tính cạnh của tam giác vuông.
Tính số đo góc.
Chứng minh hệ thức lượng giác.
Giải bài toán thực tế liên quan đến chiều cao, khoảng cách.
Bài tập tổng hợp có đáp án chi tiết.

6. Học sinh thường mắc lỗi gì khi giải bài tập lượng giác trong tam giác vuông?

Một số lỗi phổ biến gồm:

Xác định nhầm cạnh đối và cạnh kề.
Áp dụng sai công thức lượng giác.
Đổi sai đơn vị góc trên máy tính.
Làm tròn kết quả không đúng yêu cầu.
Chọn nhầm tỉ số lượng giác khi tính cạnh hoặc góc.

---------------------------------------

Như vậy, việc nắm vững cách tính tỉ số lượng giác của góc nhọn, cùng phương pháp tính cạnh và tính góc của tam giác vuông, sẽ giúp học sinh chủ động hơn khi giải toán hình học. Đây là nền tảng quan trọng để giải quyết các dạng toán nâng cao hơn trong chương trình THCS cũng như trong đề thi vào lớp 10.

Để học tốt phần này, học sinh nên luyện tập nhiều dạng bài từ cơ bản đến nâng cao, kết hợp ghi nhớ công thức lượng giác và áp dụng vào giải quyết các bài toán thực tế. Chỉ cần kiên trì luyện tập, các em sẽ dễ dàng chinh phục chuyên đề hệ thức lượng trong tam giác vuông, đạt điểm cao trong học tập và kỳ thi.

Tải về

Chọn file muốn tải về: