Chứng minh một đường thẳng luôn đi qua một điểm cố định khi điểm M di động
Cách xác định điểm cố định khi M di chuyển
Trong chương trình Toán 9, dạng bài chứng minh một đường thẳng luôn đi qua một điểm cố định khi điểm M di động là một chuyên đề hình học nâng cao, giúp học sinh phát triển tư duy suy luận hình học và kỹ năng chứng minh quỹ tích. Bài toán thường xuất hiện trong đề thi học sinh giỏi và ôn thi vào lớp 10, yêu cầu vận dụng định nghĩa, hệ thức lượng và tính chất đường tròn, tam giác để chỉ ra rằng một đường thẳng có vị trí không đổi dù điểm M thay đổi vị trí.
Bài tập 1. Cho đường tròn 
\((O;R)\) một đường thả̉ng \(d\) cắt đường tròn \((O)\) tại hai điểm \(D\) và \(E\). Một điểm \(A\) di động trên đường thả̉ng \(d\) và \(A\) nằm ngoài đường tròn \((O)\), kẻ hai tiếp tuyến \(AB\), \(AC\) đến đường tròn (\(B\), \(C\) là hai tiếp điểm). Gọi \(I\) là trung điểm của \(DE\), đường thẳng \(OI\) cắt đường thẳng \(BC\) tại \(N\). Chứng minh rằng: Khi \(A\) di động trên đường thả̉ng \(d\) thì \(BC\) luôn đi qua một điểm cố định.
Hướng dẫn giải
Hình vẽ minh họa:
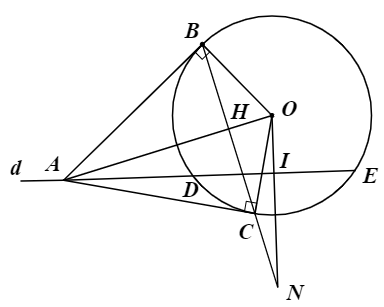
Ta có: \(I\) là trung điểm của \(DE(gt)\)
\(\Rightarrow OI\bot DE\) hay \(\Delta OIA\) vuông tại \(I\)
Gọi \(H\) là giao điểm của \(OA\) và \(BC\).
Ta có \(\Delta OHN\) vuông tại \(H\)
Ta có \(\Delta OHN\sim\Delta OIA\) (g.g) \(\Rightarrow \frac{ON}{OA} =
\frac{OH}{OI} \Rightarrow ON = \frac{OA.OH}{OI}\).
Xét \(\Delta ABO\) và \(\Delta HBO\) có: \(\widehat{ABO} = \widehat{BOH} =
90^{\circ}\), \(\widehat{AOB}\) chung
Do đó \(\Delta ABO\sim\Delta BHO\) (g.g) \(\Rightarrow \frac{OB}{OH} =
\frac{OA}{OB}\) \(\Rightarrow OA.OH =
OB^{2} = R^{2}\)
Do đó \(ON = \frac{R^{2}}{OI}\) (không đổi), \(d\) cho trước, \(O\) cố định \(\Rightarrow I\) cố định \(\Rightarrow N\) cố định.
Bài tập 2: Cho đường tròn \((O;R)\), từ một điểm \(A\) trên \((O)\) kẻ tiếp tuyến d với \((O)\). Trên đường thẳng d lấy điểm M bất kì (M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ \(AC\bot MB,\ BD\bot
MA\), gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.
1. Chứng minh tứ giác AMBO nội tiếp.
2. Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn .
3. Chứng minh: \(OI.OM = R^{2};OI.\ IM =
IA^{2}\).
4. Chứng minh OAHB là hình thoi.
5. Chứng minh ba điểm \(O,H,M\) thẳng hàng.
6. Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d.
Hướng dẫn giải
Hình vẽ minh họa:
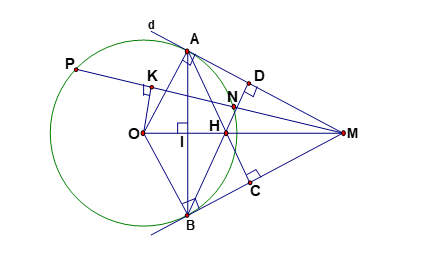
1. (Học sinh tự chứng minh)
2. Vì K là trung điểm NP nên \(OK\bot
NP\) (quan hệ đường kính và dây cung)
\(\ \Rightarrow \widehat{OKM} =
90^{0}\).
Theo tính chất tiếp tuyến ta có \(\widehat{OAM} = 90^{0};\widehat{OBM} =
90^{0}\).
Như vậy \(K;A,B\) cùng nhìn OM dưới một góc 900 nên cùng nằm trên đường tròn đường kính OM.
Vậy năm điểm \(O,K,A,M,B\) cùng nằm trên một đường tròn.
3. Ta có \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau); \(OA = OB =
R\)
OM là trung trực của AB \(\Rightarrow
OM\bot AB\) tại I .
Theo tính chất tiếp tuyến ta có \(\widehat{OAM} = 90^{0}\) nên tam giác OAM vuông tại A có AI là đường cao.
Áp dụng hệ thức giữa cạnh và đường cao \(\Rightarrow OI.\ IM = OA^{2}\) hay\(OI.OM = R^{2}\); và \(OI.\ IM = IA^{2}\).
4. Ta có \(OB\bot MB\) (tính chất tiếp tuyến) và \(AC\bot MB\); (gt)
\(\Rightarrow OB//AC\) hay \(OB\ //\ AH\).
OA ⊥ MA (tính chất tiếp tuyến) ; BD ⊥ MA (gt)
=> OA // BD hay OA // BH.
Tứ giác OAHB là hình bình hành; lại có OA = OB (= R) => OAHB là hình thoi.
5. Theo trên OAHB là hình thoi. => OH ⊥ AB; cũng theo trên OM ⊥ AB
=> O, H, M thẳng hàng (vì qua O chỉ có một đường thẳng vuông góc với AB).
6. Theo trên OAHB là hình thoi.
=> AH = AO = R.
Vậy khi M di động trên d thì H cũng di động nhưng luôn cách A cố định một khoảng bằng R.
Do đó quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A bán kính AH = R
Bài tập 3. Cho đường tròn (O) bán kính R có hai đường kính AB và CD vuông góc với nhau. Trên đoạn thẳng AB lấy điểm M (M khác O). CM cắt (O) tại N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở P. Chứng minh:
1. Tứ giác OMNP nội tiếp.
2. Tứ giác CMPO là hình bình hành.
3. CM. CN không phụ thuộc vào vị trí của điểm M.
4. Khi M di chuyển trên đoạn thẳng AB thì P chạy trên đoạn thẳng cố định nào.
Hướng dẫn giải
Hình vẽ minh họa:
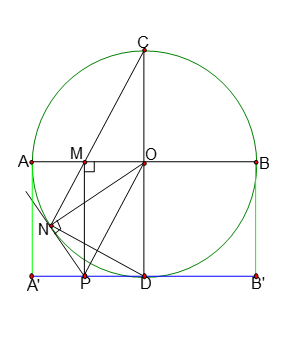
1. Ta có \(\widehat{OMP} = 90^{0}\) (vì PM ⊥ AB ); \(\widehat{ONP} =
90^{0}\) (vì NP là tiếp tuyến).
Như vậy M và N cùng nhìn OP dưới một góc bằng 900
=> M và N cùng nằm trên đường tròn đường kính OP => Tứ giác OMNP nội tiếp.
2. Tứ giác OMNP nội tiếp \(\Rightarrow
\widehat{OPM} = \widehat{ONM}\) (nội tiếp chắn cung OM)
Tam giác ONC cân tại O vì có \(ON = OC = R
= > \widehat{ONC} = \widehat{OCN}\)
\(\Rightarrow \widehat{OPM} =
\widehat{OCM}\).
Xét hai tam giác OMC và MOP ta có:
\(\widehat{MOC} = \widehat{OMP} =
90^{0}\)
\(\widehat{OPM} = \widehat{OCM}
\Rightarrow \widehat{CMO} = \widehat{POM}\)
MO là cạnh chung
\(\Rightarrow \Delta OMC = \Delta MOP
\Rightarrow OC = MP\ \ (1)\)
Theo giả thiết ta có: \(CD\bot AB;\ PM\bot
AB \Rightarrow CO//PM\ \ \ (2)\)
Từ (1) và (2) => Tứ giác CMPO là hình bình hành.
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
--------------------------------------------------
Bài toán chứng minh đường thẳng luôn đi qua điểm cố định khi điểm M di động là một nội dung quan trọng trong chuyên đề hình học Toán 9 nâng cao. Khi hiểu rõ bản chất và phương pháp chứng minh, bạn sẽ dễ dàng nhận dạng và giải quyết các bài toán quỹ tích, cực trị và chứng minh hình học tương tự.
