Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Tính các yếu tố còn lại của tam giác vuông khi biết một số yếu tố

Bài tập Toán 9 Hệ thức lượng trong tam giác có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Loại File: Word

Phân loại: Tài liệu Tính phí

Giải bài tập hệ thức lượng trong tam giác vuông Toán 9

Trong chương trình Toán 9, chuyên đề Hệ thức lượng trong tam giác vuông là nền tảng giúp học sinh rèn kỹ năng tính toán nhanh và chính xác. Bài viết Tính các yếu tố còn lại của tam giác vuông khi biết một số yếu tố tổng hợp các dạng bài tập điển hình, hướng dẫn chi tiết cách áp dụng công thức hệ thức lượng, kèm đáp án giải chi tiết giúp học sinh hiểu bản chất và tự tin vận dụng vào các bài toán thực tế.

A. Phương pháp giải toán

Phương pháp: Dùng các hệ thức lượng trong tam giác vuông

Cho tam giác $ABC$ vuông tại $A,$ $AH$ là đường cao.

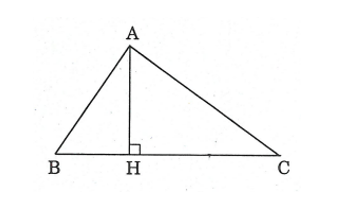
Ta có các hệ thức sau:

$BC^{2} + AB^{2} + AC^{2}$ $BC^{2} + AB^{2} + AC^{2}$ (định lý Pythagore)

$AB^{2} = BH.BC$ $AB^{2} = BH.BC$

$AC^{2} = CH.BC$ $AC^{2} = CH.BC$

$AH^{2} = HB.HC$ $AH^{2} = HB.HC$

$AH.BC = AB.AC$

$\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}}$ $\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}}$

$AC = BC.\sin B$ $AC = BC.\sin B$;

$AB = BC.\sin C$ $AB = BC.\sin C$;

$AC = BC.\cos C$ $AC = BC.\cos C$;

$AB = BC.\cos B$ $AB = BC.\cos B$;

$AB = AC.\tan C = AC.\cot B$ $AB = AC.\tan C = AC.\cot B$

$AC = AB.\tan B = AB.\cot C$ $AC = AB.\tan B = AB.\cot C$

B. Ví dụ minh họa tìm các yếu tố còn lại của tam giác vuông

Ví dụ 1: Cho $\Delta ABC$ $\Delta ABC$ vuông tại $A,$ $AH$ là đường cao và có $BH = 1,AC = 2\sqrt{5}$ $BH = 1,AC = 2\sqrt{5}$. Tính $AB,BC,AH$.

Hướng dẫn giải

Hình vẽ minh họa:

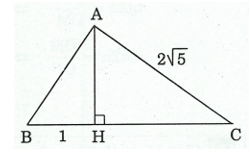
Ta có:

$CA^{2} = CB.CH = CH(CH + HB)$ $CA^{2} = CB.CH = CH(CH + HB)$

$\Rightarrow 20 = CH.(CH + 1) \Rightarrow CH = 4$ $\Rightarrow 20 = CH.(CH + 1) \Rightarrow CH = 4$

$\Rightarrow BC + BH + HC = 1 + 4 = 5$ $\Rightarrow BC + BH + HC = 1 + 4 = 5$

$AB^{2} = BH.BC \Rightarrow AB = \sqrt{5}$ $AB^{2} = BH.BC \Rightarrow AB = \sqrt{5}$

$\Rightarrow AH = \frac{AB.AC}{BC} = 2$ $\Rightarrow AH = \frac{AB.AC}{BC} = 2$.

Ví dụ 2: Tam giác $ABC$ vuông tại $A$ có đường cao $AH = \frac{12}{5}cm$ $AH = \frac{12}{5}cm$ và $\frac{AB}{AC} = \frac{3}{4}$ $\frac{AB}{AC} = \frac{3}{4}$. Tính bán kính $R$ của đường tròn ngoại tiếp tam giác $ABC$.

Hướng dẫn giải

Tam giác $ABC$ vuông tại $A,$ có đường cao $AH \Rightarrow AB.AC = AH^{2}\ \ \ (*)$ $AH \Rightarrow AB.AC = AH^{2}\ \ \ (*)$

Mặt khác $\frac{AB}{AC} = \frac{3}{4} \Leftrightarrow AB = \frac{3}{4}AC$ $\frac{AB}{AC} = \frac{3}{4} \Leftrightarrow AB = \frac{3}{4}AC$ thế vào $(*),$ ta được:

$\frac{3}{4}AC^{2} = \left( \frac{12}{5} \right)^{2} \Leftrightarrow AC = \frac{8\sqrt{3}}{5}$ $\frac{3}{4}AC^{2} = \left( \frac{12}{5} \right)^{2} \Leftrightarrow AC = \frac{8\sqrt{3}}{5}$.

Suy ra $AB = \frac{3}{4}.\frac{8\sqrt{3}}{5} = \frac{6\sqrt{3}}{5} \Rightarrow BC = \sqrt{AB^{2} + AC^{2}} = 2\sqrt{3}$ $AB = \frac{3}{4}.\frac{8\sqrt{3}}{5} = \frac{6\sqrt{3}}{5} \Rightarrow BC = \sqrt{AB^{2} + AC^{2}} = 2\sqrt{3}$.

Vậy bán kính cần tìm là $R = \frac{BC}{2} = \sqrt{3}cm$ $R = \frac{BC}{2} = \sqrt{3}cm$

Ví dụ 3: Cho $\Delta ABC$ $\Delta ABC$ vuông tại $A,$ có đường cao $AH$ ($H$ ở trên $BC).$ Tính $AH,\ \ CH,\ \ BH,\ \ BC$ $AH,\ \ CH,\ \ BH,\ \ BC$ nếu biết $AB = 3,$ $AC = 4.$

Hướng dẫn giải

Hình vẽ minh họa:

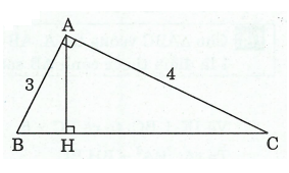
Ta có:

$\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}} = \frac{1}{9} + \frac{1}{16} = \frac{25}{144}$ $\frac{1}{AH^{2}} = \frac{1}{AB^{2}} + \frac{1}{AC^{2}} = \frac{1}{9} + \frac{1}{16} = \frac{25}{144}$

$\Rightarrow AH^{2} = \frac{144}{25} \Rightarrow AH = \frac{12}{5}$ $\Rightarrow AH^{2} = \frac{144}{25} \Rightarrow AH = \frac{12}{5}$

Xét $\Delta AHC:$ $\Delta AHC:$

$AC^{2} = AH^{2} + HC^{2}$ $AC^{2} = AH^{2} + HC^{2}$

$\Leftrightarrow HC^{2} = AC^{2} - AH^{2}$ $\Leftrightarrow HC^{2} = AC^{2} - AH^{2}$

$\Leftrightarrow HC^{2} = 16 - \frac{144}{25} = \frac{256}{25} \Rightarrow HC = \frac{16}{5}$ $\Leftrightarrow HC^{2} = 16 - \frac{144}{25} = \frac{256}{25} \Rightarrow HC = \frac{16}{5}$

Xét $\Delta ABH:$ $\Delta ABH:$ $BH^{2} = AB^{2} - AH^{2} = 9 - \frac{144}{25} = \frac{225 - 144}{25} = \frac{81}{5} \Rightarrow BH = \frac{9}{5}$ $BH^{2} = AB^{2} - AH^{2} = 9 - \frac{144}{25} = \frac{225 - 144}{25} = \frac{81}{5} \Rightarrow BH = \frac{9}{5}$

Ta có: $BC^{2} = AB^{2} + AC^{2} = 9 + 16 = 25$ $BC^{2} = AB^{2} + AC^{2} = 9 + 16 = 25$ $\Rightarrow BC = 5$ $\Rightarrow BC = 5$.

Ví dụ 4: Cho hình thang $ABCD$ với đường cao $AB.$ Biết rằng $AD = 3a,$ $BC = 4a,$ $\widehat{BDC} = 90{^\circ}.$ $\widehat{BDC} = 90{^\circ}.$ Tính $AB,$ $CD,$ $AC.$

Hướng dẫn giải

Hình vẽ minh họa:

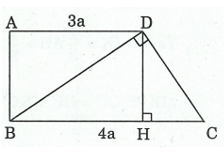
Vẽ $DH\bot BC$ $DH\bot BC$ ($H$ ở trên $BC)$ thì $ADHB$ là hình chữ nhật nên

$BH = AD = 3a$ và $AB = DH$

Xét tam giác vuông $BDC,$ ta có:

$DH^{2} = HB.HC = HB(BC - BH) = 3a(4a - 3a) = 3a^{2}$ $DH^{2} = HB.HC = HB(BC - BH) = 3a(4a - 3a) = 3a^{2}$

$\Rightarrow DH = a\sqrt{3} \Rightarrow AB = DH = a\sqrt{3}$ $\Rightarrow DH = a\sqrt{3} \Rightarrow AB = DH = a\sqrt{3}$

Ta lại có: $DC^{2} = CH.CB = a.4a = 4a^{2}$ $DC^{2} = CH.CB = a.4a = 4a^{2}$

Suy ra $DC = 2a.$

Ta lại có: $AC = \sqrt{AB^{2} + BC^{2}} = \sqrt{3a^{2} + 16a^{2}} = a\sqrt{19}.$ $AC = \sqrt{AB^{2} + BC^{2}} = \sqrt{3a^{2} + 16a^{2}} = a\sqrt{19}.$

Ví dụ 5: Cho $\Delta ABC$ $\Delta ABC$ vuông tại $C,$ $CD$ là đường cao, $DA = 9,$ $DB = 16.$ Tính $CD,\ \ AC,\ \ BC.$ $CD,\ \ AC,\ \ BC.$

Hướng dẫn giải

Hình vẽ minh họa:

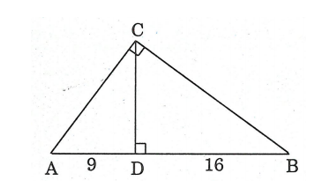
Ta có:

$DC^{2} = DA.DB = 9.16 = 144 \Rightarrow DC = 12$ $DC^{2} = DA.DB = 9.16 = 144 \Rightarrow DC = 12$

Ta có:

$AC^{2} = AB.AD = 25.9 = 225 \Rightarrow AC = 5.3 = 15$ $AC^{2} = AB.AD = 25.9 = 225 \Rightarrow AC = 5.3 = 15$

Ta có:

$CB^{2} = AB.DB = 25.16 = 400 \Rightarrow CB = 20$ $CB^{2} = AB.DB = 25.16 = 400 \Rightarrow CB = 20$

C. Bài tập tự rèn luyện có đáp án chi tiết

Bài tập 1: Cho $\Delta ABC$ $\Delta ABC$ vuông tại $A,$ $\frac{AB}{AC} = \frac{2}{3}.$ $\frac{AB}{AC} = \frac{2}{3}.$ Đường cao $AH = 6.$ Tính $HB,\ \ HC,\ \ AB,\ \ AC.$ $HB,\ \ HC,\ \ AB,\ \ AC.$

Bài tập 2: Cho $\Delta ABC$ $\Delta ABC$ vuông tại $C,$ $AD$ là đường phân giác trong, $BD = x,$ $m$ Tính $AB,\ \ BC,\ \ AC.$ $AB,\ \ BC,\ \ AC.$

Bài tập 3: Cho nửa đường tròn đường kính $AB = 2R,$ $m$ chạy trên đường tròn, đặt $\widehat{BAM} = \alpha,$ $\widehat{BAM} = \alpha,$ tiếp tuyến tại $M$ cắt $AB$ tại $N.$ Hãy tính các cạnh của tam giác $AMN.$

Bài tập 4: Cho hình thang vuông $ABCD,$ đường cao $AB.$ Ngoại tiếp đường tròn đường kính $r,$ cho $\widehat{C} = \frac{\pi}{3}.$ $\widehat{C} = \frac{\pi}{3}.$ Tính các cạnh của hình thang.

------------------------------------

Qua bài viết Tính các yếu tố còn lại của tam giác vuông khi biết một số yếu tố, học sinh sẽ nắm vững cách áp dụng hệ thức lượng trong tam giác vuông để giải các dạng bài tập nhanh và chính xác. Hãy luyện tập thường xuyên và tham khảo thêm các bài tập Toán 9 có đáp án chi tiết khác để củng cố kiến thức, chuẩn bị tốt cho các kỳ thi sắp tới!

Tải về

Chọn file muốn tải về: