Tìm điều kiện độ dài cạnh để hình khối đạt diện tích và thể tích lớn nhất

Trong quá trình học Toán, đặc biệt ở phần Hình học không gian, các dạng bài toán tìm điều kiện độ dài cạnh để hình khối đạt diện tích và thể tích lớn nhất thường xuyên xuất hiện trong đề kiểm tra và đề thi. Việc hiểu rõ phương pháp giải và các bước biến đổi không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện tư duy logic và kỹ năng tính toán nhanh. Bài viết dưới đây sẽ hướng dẫn chi tiết cách giải, kèm ví dụ minh họa cụ thể, giúp bạn dễ dàng vận dụng để đạt điểm cao.

A. Bài tập tìm điều kiện độ dài cạnh để diện tích, thể tích hình đạt max

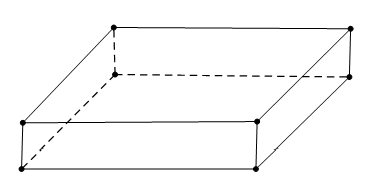
Hướng dẫn giải

Gọi chiều rộng là \(x(cm)(0 < x < 12)\)

Chiều dài là \(12 - x(cm)\)

Chiều cao là \(24 - x(cm)\)

Ta có thể tích chiếc hộp là: \(V = x(12 - x)(24 - x)\left( cm^{3} \right)\)

Bất đẳng thức Cauchy 3 số không âm \(a,b,c\) ta có:  

\(a + b + c \geq 3\sqrt[3]{abc}\)      

Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)

Thật vậy, đặt \(x = \sqrt[3]{a},y = \sqrt[3]{b},z = \sqrt[3]{c}\)

\(\Rightarrow x,y,z \geq 0 \Rightarrow x + y + z \geq 0\)

Ta phái chứng minh:

\(x^{3} + y^{3} + z^{3} \geq 3xyz\)

\((x + y)^{3} - 3xy(x + y) + z^{3} - 3xyz \geq 0\)

\((x + y + z)\left\lbrack (x + y)^{2} - (x + y)z + z^{2} \right\rbrack - 3xy(x + y + z) \geq 0\)

\((x + y + z)\left\lbrack x^{2} + y^{2} + z^{2} + 2xy - xz - yz \right\rbrack - 3xy(x + y + z) \geq 0\)

\((x + y + z)\left\lbrack x^{2} + y^{2} + z^{2} - xy - xz - yz \right\rbrack \geq 0\)

\(x^{2} + y^{2} + z^{2} - xy - xz - yz \geq 0\) (vì \(x + y + z \geq 0\))

\((x - y)^{2} + (y - z)^{2} + (z - x)^{2} \geq 0\) (luôn đúng)

Dấu “=” xảy ra khi \(x = y = z\) hay \(a = b = c\)

Áp dụng bất đẳng thức Cauchy cho 3 số không âm ta có:

\(V = x(12 - x)(24 - x)\left( cm^{3} \right)\)

\(\frac{1}{\left( \sqrt{3} - 1 \right)\left( 2 - \sqrt{3} \right)}.x.\left( \sqrt{3} - 1 \right)\left( 2 - \sqrt{3} \right)(12 - x)(24 - x)\)

\(\leq \frac{1}{\left( \sqrt{3} - 1 \right)\left( 2 - \sqrt{3} \right)}.\left\lbrack \frac{x + \left( \sqrt{3} - 1 \right)(12 - x) + \left( 2 - \sqrt{3} \right)(24 - x)}{3} \right\rbrack^{3}\)

\(= \frac{1}{\left( \sqrt{3} - 1 \right)\left( 2 - \sqrt{3} \right)}.\left\lbrack \frac{x + 12\sqrt{3} - \sqrt{3}x - 12 + x + 48 - 2x - 24\sqrt{3} + \sqrt{3}x}{3} \right\rbrack^{3}\)

\(= \frac{1}{\left( \sqrt{3} - 1 \right)\left( 2 - \sqrt{3} \right)}.\left\lbrack \frac{36 - 12\sqrt{3}}{3} \right\rbrack^{3} = 384\sqrt{3}\)

Dấu “=” xảy ra khi và chỉ khi:

\(x = \left( \sqrt{3} - 1 \right)(12 - x) = \left( 2 - \sqrt{3} \right)(24 - x)\)

\(\Leftrightarrow x = 12 - 4\sqrt{3}\)

Vậy \(V_{\max} = 384\sqrt{3} \Leftrightarrow x = 12 - 4\sqrt{3}\)

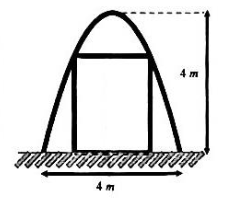
Hướng dẫn giải

Hình vẽ minh họa

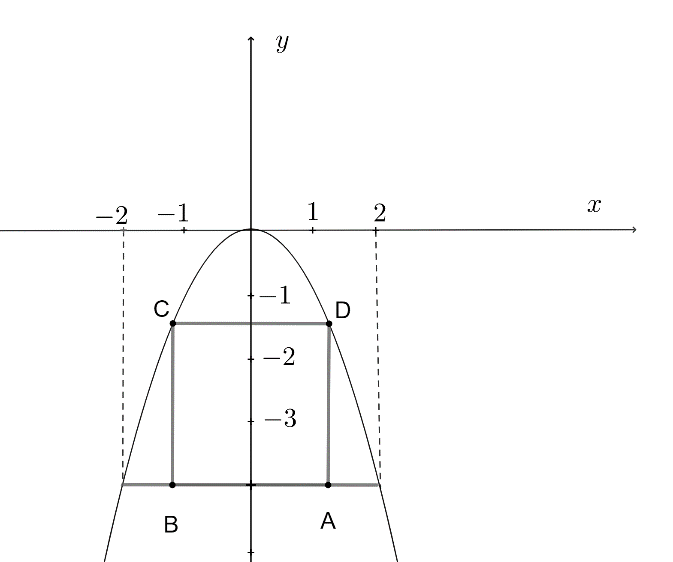
Đặt hệ trục tọa độ Oxy như hình vẽ. Parabol có dạng \(y = ax^{2}(a < 0)\)

Khoảng cách từ điểm cao nhất của cửa đến mặt đất là 4 mét, khoảng cách giữa hai chân cửa là 4 mét nên parabol đi qua điểm \((2; - 4)\)

Suy ra: \(- 4 = a.2^{2} \Leftrightarrow a = - 1\)

Parabol có dạng \(y = - x^{2}\)

Giả sử\(ABCD\) là hình chữ nhật có độ dài \(AB = CD = 2k\)

Khi đó 4 đỉnh của khung thép hình chữ nhật có tọa độ là:

\(A(k;\ - 4);\ \ B( - k; - 4);C\left( - k;\ \ k^{2} \right);D\left( k;\ \ k^{2} \right)(k > 0)\)

Suy ra \(AB = 2k;\ \ BC = 4 - k^{2}\)

Khi đó diện tích hình chữ nhật ABCD bằng \(2k\left( 4 - k^{2} \right)\)

Ta có:

\(2k\left( 4 - k^{2} \right) - \frac{32}{3\sqrt{3}} = - 2\left( k^{3} - 4k + \frac{16}{3\sqrt{3}} \right)\)

\(= - 2\left( k^{2} - 2k.\frac{2}{\sqrt{3}} + \frac{4}{3} \right).\left( k + \frac{4}{\sqrt{3}} \right)\)

\(= - 2\left( k - \frac{2}{\sqrt{3}} \right)^{2}\left( k + \frac{4}{\sqrt{3}} \right) \leq 0\) với \(k > 0\)

Suy ra \(2k\left( 4 - k^{2} \right) \leq \frac{32}{3\sqrt{3}}\)

Dấu “=” có khi \(k = \frac{2}{\sqrt{3}}\).

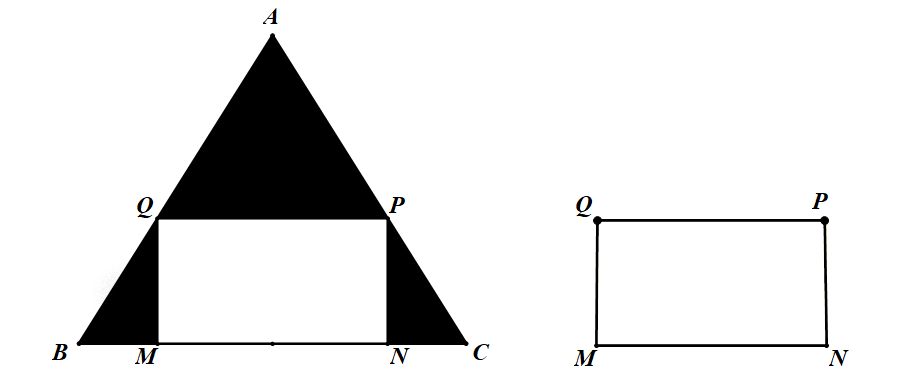
Hướng dẫn giải

Gọi độ dài đoạn \(MB\) là \(x(cm)\), ta có:

Độ dài đoạn \(NC\) là \(x(cm)\)

Độ dài đoạn \(MN\) là \(20 - x - x = 20 - 2x(cm)\)

Tam giác \(BQM\) vuông tại \(M\) có: \(\tan B = tan60^{0} = \frac{QM}{BM} = \frac{QM}{x}\)

\(QM = x.tan60^{0} = x.\sqrt{3}\)

Diện tích hình chữ nhật \(MNPQ\) là: \(S = MN.QM = (20 - 2x).x\sqrt{3}\)

Áp dụng bất đẳng thức Cauchy ta có:

\(S = (20 - 2x).x\sqrt{3} = 2\sqrt{3}(10 - x).x \leq 2\sqrt{3}\left( \frac{10 - x + x}{2} \right)^{2}\)

\(S \leq 2\sqrt{3}.25 = 50\sqrt{3}\)

Dấu bằng xảy ra khi \(10 - x = x \Leftrightarrow x = 5\)

Vậy \(MB = 5cm\) để hình chữ nhật \(MNPQ\) có diện tích lớn nhất.

B. Bài tập tự rèn luyện tìm điều kiện cạnh hình khối có hướng dẫn chi tiết

Bài tập 1. Một hình hộp chữ nhật có các kích thước a; b; c như hình vẽ:

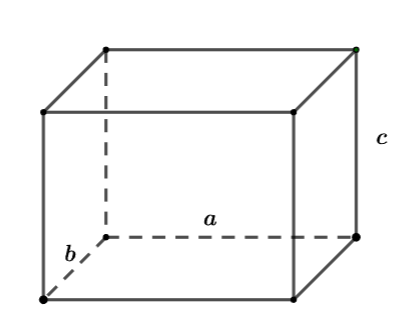
Biết tổng diện tích tất cả các mặt bằng 36 và \(a^{2} + b^{2} + c^{2} = 36,c = 2\sqrt{2}\). Tìm \(a,\ \ b\) để thể tích khối hộp là lớn nhất, khi đó thể tích khối hộp là bao nhiêu?

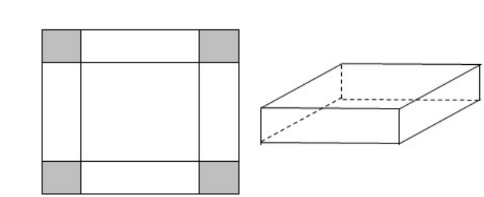
Bài tập 2. Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x ( cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để thể tích của hộp là lớn nhất.

Bài tập 3. Người ta cần làm một cái bồn chứa dạng hình trụ có thể tích \(1000\)lít bằng inox để chứa nước, tính bán kính của hình trụ đó sao cho diện tích toàn phần của bồn chứa đó là nhỏ nhất?

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

---------------------------------------------------------------

Qua bài viết, chúng ta đã tìm hiểu cách tìm điều kiện cạnh để diện tích và thể tích hình khối đạt giá trị lớn nhất, đồng thời nắm rõ phương pháp áp dụng vào từng dạng toán cụ thể. Đây là kiến thức quan trọng không chỉ giúp giải nhanh các bài tập mà còn là nền tảng để xử lý các đề nâng cao. Hãy luyện tập thường xuyên để thành thạo và đạt kết quả tốt nhất trong các kỳ thi Toán.