VnDoc.com

Bài Toán Xác Suất Thống Kê Ôn Thi Vào 10 Có Đáp Án – Tổng Hợp Các Dạng Hay Gặp

Chuyên đề Toán 9 ôn thi vào 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Ôn thi vào 10: Các dạng bài xác suất thống kê lớp 9

Phần I. Đề bài toán thống kê, xác suất
Phần II. Đáp án bài tập thống kê xác suất

Xác suất – thống kê là chuyên đề quan trọng trong chương trình Toán 9 ôn thi vào 10, xuất hiện thường xuyên trong đề thi của các trường công lập và chuyên. Nhiều học sinh gặp khó khăn khi phân loại bài, đặc biệt là các dạng liên quan đến tổ hợp, biến cố, không gian mẫu và tính xác suất. Bài viết này tổng hợp trọn bộ bài toán xác suất – thống kê có đáp án chi tiết, kèm phương pháp giải dễ hiểu và các dạng bài hay gặp nhất giúp bạn học nhanh, ôn kỹ và làm bài thi tự tin hơn.

Phần I. Đề bài toán thống kê, xác suất

Bài tập 1. 1). Một cuộc điều tra về thời gian một nhóm học sinh làm một bài kiểm tra trắc nghiệm cho kết quả như sau:

Thời gian (phút)	$\lbrack 0;5)$ $\lbrack 0;5)$	$\lbrack 5;10)$ $\lbrack 5;10)$	$\lbrack 10;15)$ $\lbrack 10;15)$	$\begin{matrix} \lbrack 15,20) \end{matrix}$ $\begin{matrix} \lbrack 15,20) \end{matrix}$
Tần số	1	5	9	5

Cho biết có bao nhiêu học sinh tham gia điều tra và lập bảng tần số tương đối ghép nhóm cho kết quả điều tra

2) Một toà nhà chung cư có 30 tầng, được đánh số lần lượt từ 1 đến 30. Bạn Bình vào thang máy ở tầng 1, bấm chọn ngẫu nhiên số một tầng để đi lên. Tính xác suất của các biến cố A: “Bình đi lên tầng có số là một số nguyên tố”.

Bài tập 2. Một bác thợ đóng giày thống kê lại độ dài bàn chân (đơn vị: cm) của 60 khách hàng ở bảng tần số ghép nhóm như sau:

Nhóm	$\lbrack 27;28)$ $\lbrack 27;28)$	$\lbrack 28;29)$ $\lbrack 28;29)$	$\lbrack 29;30)$ $\lbrack 29;30)$	$\lbrack 30;31)$ $\lbrack 30;31)$	Cộng
Tần số $(n)$	$8$	$18$	$24$	$10$	$60$

1) Tìm tần số tương đối của mỗi nhóm.

2) Lập bảng tần số tương đối ghép nhóm cho mẫu số liệu trên.

3) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột biểu diễn mẫu số liệu trên.

Bài tập 3. Xúc xắc là một khối nhỏ hình lập phương được đánh dấu

chấm tròn với số lượng từ một đến sáu chấm cho cả sáu mặt. Bạn Khôi gieo viên xúc xắc được làm bằng gỗ nguyên khối hai lần liên tiếp và theo dõi số chấm xuất hiện trên viên xúc xắc.

Kết quả được xác định bởi một cặp số $(x,y)$; $\left( x,y \in N^{*};x,y \leq 6 \right)$ $\left( x,y \in N^{*};x,y \leq 6 \right)$tương ứng với số chấm xuất hiện trên viên xúc xắc sau hai lần gieo.

Ví dụ: Lần thứ nhất gieo được mặt $2$ chấm, lần thứ hai gieo được mặt $5$chấm thì kết quả là $(2;5)$

a) Liệt kê các kết quả có thể xảy ra để số chấm xuất hiện sau hai lần gieo là giống nhau.

b) Tính xác xuất để tổng số chấm xuất hiện sau hai lần gieo bằng $7$. Biết rằng xác suất P được tính theo công thức:

P(A) = (Số khả năng xảy ra của A) : (Tất cả các khả năng xảy ra)

Bài tập 4. Sau khi thống kê độ dài (đơn vị: centimét) của $60$ lá dương xỉ trưởng thành, người ta có bảng tần số ghép nhóm như sau:

Nhóm	$\lbrack 10;20)$ $\lbrack 10;20)$	$\lbrack 20;30)$ $\lbrack 20;30)$	$\lbrack 30;40)$ $\lbrack 30;40)$	$\lbrack 40;50\rbrack$ $\lbrack 40;50\rbrack$	Cộng
Tần số $(n)$	$8$	$18$	$24$	$10$	$60$

a) Tìm tần số tương đối của mỗi nhóm.

b) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.

c) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.

Bài tập 5.

1) Bảng thống kê sau cho biết số lượng các thiên tai xảy ra tại Việt Nam giai đoạn 1990 - 2021.

Loại thiên tai	Hạn hán	Bệnh dịch	Lũ lụt	Sạt lở đất	Bão
Số lượng	6	9	71	6	94

(Theo Vietnam.opendevelopmentmekong.net)

Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng biểu điễn số liệu đã cho.

Bài tập 6. Có năm đoạn thẳng có độ dài lần lượt là $2;4;6;8;10(cm)$. Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng trên. Tính xác suất của biến cố $E$: “Ba đoạn thẳng được lấy ra lập thành ba cạnh của một tam giác”

Bài tập 7.Kết quả đo chiều cao của $100$ cây keo $3$ năm tuổi tại một nông trường được cho ở bảng sau:

Chiều cao (m)	$\lbrack 8,4;8,6)$ $\lbrack 8,4;8,6)$	$\lbrack 8,6;8,8)$ $\lbrack 8,6;8,8)$	$\lbrack 8,8;9,0)$ $\lbrack 8,8;9,0)$	$\lbrack 9,0;9,2)$ $\lbrack 9,0;9,2)$	$\lbrack 9,2;9,4)$ $\lbrack 9,2;9,4)$	Tổng
Số cây	$5$	$12$	$25$	$44$	$14$	$100$

a) Lập bảng tần số tương đối ghép nhóm.

b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê thu được ở câu a.

Bài tập 8. Một hộp có $20$ thể cùng loại, mỗi thẻ được ghi một trong các số $1;\ 2;\ 3;\ 4;\ 5;\ \ldots\ ;\ 20$ $1;\ 2;\ 3;\ 4;\ 5;\ \ldots\ ;\ 20$, hai thẻ khác nhau thì ghi số khác nhau .Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:

a) Biến cố A: “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng là $2$”.

b) Biến cố B: “Số xuất hiện trên thẻ được rút ra là số nguyên tố”.

c) Biến cố C: “Số xuất hiện trên thẻ được rút ra là số có hai chữ số với tích các chữ số bằng $4$”.

Bài tập 9. 1) Biểu đồ bên biểu diễn tỉ lệ đại biểu tham dự hội nghị theo độ tuổi. Biết rằng có $54$ đại biểu từ $25$ đến $35$ tuổi.

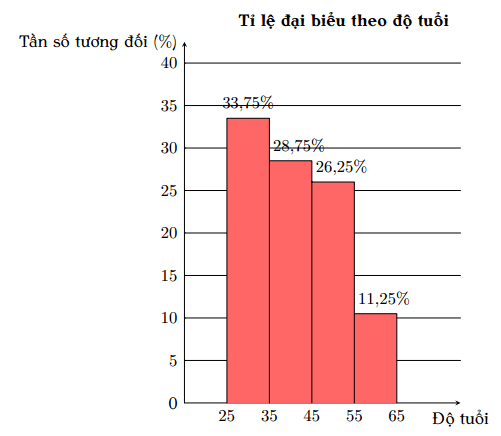
Có bao nhiêu đại biểu tham dự hội nghị? Lập bảng tần số ghép nhóm tương ứng.

2) Xét phép thử quay bánh xe và quan sát xem khi nó dừng thì mũi kim (được gắn cố định) chỉ vào ô số mấy. Tính xác suất của các biến cố A: “Kim chỉ vào ô có số là bội của 3”?

Bài tập 10. 1) Biểu đồ hình quạt tròn dưới đây biểu diễn tần số tương đối của các môn thể thao được yêu thích của học sinh THCS của $1$ trường hiện nay:

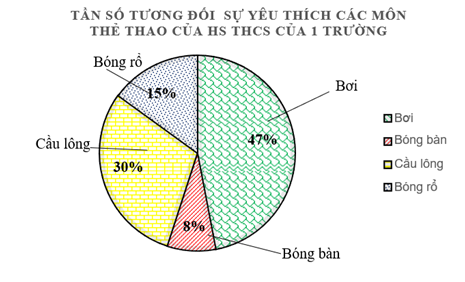
a) Hãy lập bảng tần số tương đối của biểu đồ trên.

b) Môn thể thao nào được học sinh THCS của $1$ trường yêu thích nhất? Vì sao?

2) Một hộp chứa $1$ viên bi xanh, $1$ viên bi đỏ và $1$ viên bi trắng. Các viên bi có cùng kích thước và khối lượng. An lần lượt lấy ra ngẫu nhiên từng viên bi từ trong hộp cho đến khi hết bi.

a. Xác định không gian mẫu của phép thử.

b. Tính xác suất của mỗi biến cố sau:

A: “Viên bi màu đỏ được lấy ra sau cùng”.

B: “Viên bi màu trắng được lấy ra trước viên bi màu đỏ”.

C: “Viên bi lấy ra đầu tiên không phải màu xanh”.

Còn tiếp

Phần II. Đáp án bài tập thống kê xác suất

Bài tập 1.

1). Có tất cả: $1 + 5 + 9 + 5 = 20$ học sinh tham gia

Bảng tần số tương đối ghép nhóm cho kết quả trên là:

Thời gian (phút)	$\lbrack 0;5)$ $\lbrack 0;5)$	$\lbrack 5;10)$ $\lbrack 5;10)$	$\lbrack 10;15)$ $\lbrack 10;15)$	$\lbrack 15,20)$ $\lbrack 15,20)$
Tần số tương đối	$5\%$ $5\%$	$25\%$ $25\%$	$45\%$ $45\%$	$25\%$ $25\%$

2). Không gian mẫu của phép thử là $\Omega = \left\{ 2;3;...;29;30 \right\}$ $\Omega = \left\{ 2;3;...;29;30 \right\}$. $\Omega$ $\Omega$ có $29$ phần tử.

Các kết quả của phép thử là đồng khả năng.

Có 10 kết quả thuận lợi cho biến cố A là: $2;\ 3;\ 5;\ 7;\ 11;\ 13;\ 17;\ 19;\ 23;\ 29$ $2;\ 3;\ 5;\ 7;\ 11;\ 13;\ 17;\ 19;\ 23;\ 29$.

Xác suất của biến cố A là $P(A) = \frac{10}{29}$ $P(A) = \frac{10}{29}$.

Bài tập 2.

1) Tần số tương đối của các nhóm lần lượt là:

$f_{1} = \frac{8.100}{60}\% = 13,33\%;f_{2} = \frac{18.100}{60}\% = 30\%$ $f_{1} = \frac{8.100}{60}\% = 13,33\%;f_{2} = \frac{18.100}{60}\% = 30\%$

$f_{3} = \frac{24.100}{60}\% = 40\%;f_{4} = \frac{10.100}{60}\% = 16,67\%$ $f_{3} = \frac{24.100}{60}\% = 40\%;f_{4} = \frac{10.100}{60}\% = 16,67\%$

2) Bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó:

Nhóm	$\lbrack 27;28)$ $\lbrack 27;28)$	$\lbrack 28;29)$ $\lbrack 28;29)$	$\lbrack 29;30)$ $\lbrack 29;30)$	$\lbrack 30;31)$ $\lbrack 30;31)$	Cộng
Tần số tương đối $(\%)$ $(\%)$	$13,33$	$30$	$40$	$16,67$	$100$

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-------------------------------------------

Hy vọng tài liệu tổng hợp bài toán xác suất – thống kê ôn thi vào 10 kèm lời giải chi tiết ở trên đã giúp bạn củng cố kiến thức, nắm chắc phương pháp và rèn luyện kỹ năng phân dạng bài. Đây là những dạng toán cơ bản nhưng rất dễ ghi điểm trong đề thi tuyển sinh lớp 10. Bạn hãy tiếp tục luyện tập theo từng chuyên đề Toán 9 để đạt kết quả cao và hoàn thành mục tiêu vào trường mong muốn.

Xem thử Tải về

Chọn file muốn tải về: