Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Tìm vị trí điểm M để tam giác có diện tích lớn nhất, nhỏ nhất

Chuyên đề ôn thi Toán 9 vào 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập Toán 9: Tìm M để diện tích tam giác lớn nhất, nhỏ nhất

Trong chương trình Toán lớp 9, các bài toán liên quan đến tìm giá trị lớn nhất và nhỏ nhất trong hình học là dạng bài thường xuyên xuất hiện trong các đề kiểm tra và đặc biệt là đề thi tuyển sinh vào lớp 10 môn Toán. Một trong những dạng toán tiêu biểu mà học sinh thường gặp là tìm vị trí điểm M để tam giác có diện tích lớn nhất hoặc nhỏ nhất.

Dạng toán này không chỉ yêu cầu học sinh nắm vững kiến thức về diện tích tam giác, đường cao, quan hệ hình học, mà còn cần biết vận dụng linh hoạt các phương pháp như biến đổi hình học, sử dụng bất đẳng thức, hoặc khai thác tính chất đường vuông góc. Nếu hiểu đúng bản chất bài toán, học sinh có thể tìm ra lời giải ngắn gọn và chính xác.

Trong bài viết này, chúng tôi sẽ tổng hợp phương pháp giải dạng toán tìm vị trí điểm M để tam giác có diện tích lớn nhất, nhỏ nhất, kèm theo các ví dụ minh họa và bài tập vận dụng. Đây là chuyên đề ôn thi Toán 9 vào 10 quan trọng, giúp học sinh rèn luyện tư duy hình học và nâng cao kỹ năng giải bài toán cực trị trong hình học.

A. Công thức tính diện tích cần nhớ

Diện tích tam giác

$S = \frac{1}{2}a.h$
$S = \frac{1}{2}ab\sin C = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A$
$S = \sqrt{p(p - a)(p - b)(p - c)}$ với $p = \frac{a + b + c}{2}$
$a = 2R\sin A$ , $b = 2R\sin B,c = 2R\sin C$ …

Diện tích hình chữ nhật

Diện tích hình thang

$S = \frac{1}{2}(a + b)h$

Diện tích hình vuông

$S = a^{2}$

B. Các công thức bất đẳng thức

Ở cấp THCS, các em học sinh được làm quen với bất đẳng thức Cauchy dạng 2 số hoặc 3 số. Để giải quyết tốt các bài toán hình học: Ta cần nắm chắc một số kết quả quan trọng sau:

Cho các số thực dương a; b

$a + b \geq 2\sqrt{ab} \Leftrightarrow ab \leq \left( \frac{a + b}{2} \right)^{2} \Leftrightarrow (a + b)^{2} \geq 4ab$

Dấu bằng xảy ra khi và chỉ khi a = b

$\frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b} \geq \frac{2\sqrt{2}}{\sqrt{a^{2} + b^{2}}}$ ; $\frac{x^{2}}{a} + \frac{y^{2}}{b} \geq \frac{(x + y)^{2}}{a + b}$
$a^{2} + ab + b^{2} = \frac{3}{4}(a + b)^{2} + \frac{1}{4}(a - b)^{2} \geq \frac{3}{4}(a + b)^{2}$
$a^{2} - ab + b^{2} = \frac{1}{4}(a + b)^{2} + \frac{3}{4}(a - b)^{2} \geq \frac{1}{4}(a + b)^{2}$

Cho các số thực dương a; b; c:

$a + b + c \geq 3\sqrt[3]{abc} \Leftrightarrow abc \leq \left( \frac{a + b + c}{3} \right)^{3}$

Dấu bằng xảy ra khi và chỉ khi a = b = c.

$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq \frac{9}{a + b + c} \geq \frac{3\sqrt{3}}{\sqrt{a^{2} + b^{2} + c^{2}}}$

$ab + bc + ca \leq \frac{(a + b + c)^{2}}{3} \leq a^{2} + b^{2} + c^{2}$

$\frac{x^{2}}{a} + \frac{y^{2}}{b} + \frac{z^{2}}{c} \geq \frac{(x + y + z)^{2}}{a + b + c}$

C. Bài tập tìm điểm M để diện tích tam giác lớn nhất, nhỏ nhất

Bài 1: Cho tam giác ABC có AB = a, CA = b, AB = c. M là một điểm thuộc miền trong tam giác ABC. Gọi E; F; K lần lượt là hình chiếu vuông góc của M trên .BC; CA, AB Xác định vị trí điểm M để tích ME, MF, MK đạt giá trị lớn nhất.

Hướng dẫn giải

Hình vẽ minh họa

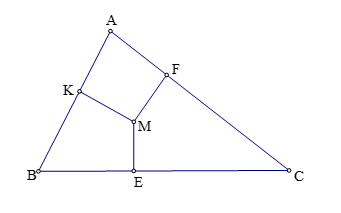
Ta có:

$2S_{ABC} = 2\left( S_{MBC} + S_{MCA} + S_{MAB} \right)$ .

= a.ME + b.MF + c.MK

Do đó áp dụng bất đẳng thức Cô-si

với bộ 3 số a.ME, b.MF, c.MK.

Ta có:

$a.b.c.ME.MF.MK = (a.ME).(b.MF).(c.MK) \leq \frac{1}{27}(a.ME + b.MF + c.MK)^{3} = 8S_{ABC}^{3}$

$\Rightarrow ME.MF.MK \leq \frac{8S_{ABC}^{3}}{abc}$ .

Dấu “=” xảy ra khi và chỉ khi a.ME = b.MF = c.MK

$\Leftrightarrow S_{MBC} = S_{MCA} = S_{MAB} \Leftrightarrow M$ là trọng tâm tam giác ABC.

Vậy $\max(ME.MF.MK) = \frac{8S_{ABC}^{3}}{abc}$ khi M là trọng tâm tam giác ABC.

Bài 2: Cho tam giác ABC cân đỉnh A. Gọi O là trung điểm của BC. Đường tròn (O) tiếp xúc với AB ở E tiếp xúc với AC ở F. Điểm H chạy trên cung nhỏ $\widehat{E F}$ tiếp tuyến của đường tròn tại H cắt AB, AC lần lượt tại M, N. Xác định vị trí của điểm H để diện tích tam giác AMN đạt giá trị lớn nhất.

Hướng dẫn giải

Hình vẽ minh họa

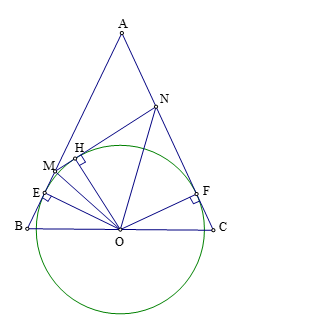
Dễ thấy OM, ON lần lượt là phân giác $\widehat{EOM},\widehat{FOH}$ .

Từ đó ta có:

$\widehat{MON} = \frac{180^{0} - \widehat{BAC}}{2} = \widehat{ABC} \Rightarrow \Delta MBO\sim\Delta OCN$ (g - g) $\Rightarrow \frac{MB}{OC} = \frac{BO}{CN} \Rightarrow BM.CN = OB.OC = \frac{BC^{2}}{4} = const$ (1)

Ta lại có $S_{AMN} = S_{ABC} - S_{BMNC}$ nên $S_{AMN}$ đạt giá trị lớn nhất khi và chỉ khi $S_{BMNC}$ đạt giá trị nhỏ nhất.

Gọi R là bán kính của đường tròn (O), ta có:

$S_{BMNC} = S_{BOM} + S_{MON} + S_{NOC}$

$= \frac{1}{2}R(BM + MN + NC)$

$=\frac{1}{2}R\left\lbrack BE + CF + 2(EM + FN) \right\rbrack$ (vì MN = EM + FN = R(BE + EM + FN); BE = CF)

= R(BE + BM + CN - 2BE) = R(BM + CN - BE) (2)

Áp dụng bất đẳng thức Cauchy, từ (1) và (2) suy ra:

$S_{BMNC} \geq R\left( \sqrt{BM.CN} - BE \right) = R\left( \frac{BC}{2} - BE \right)$ .

Dấu “=” xảy ra khi và chỉ khi BM = CN ⇔MN / / BC khi và chỉ khi H là giao điểm của đường trung trực của BC với đường tròn (O).

Vậy diện tích tam giác AMN đạt giá trị lớn nhất khi H là giao của đường trung trực của BC với đường tròn (O).

C. Bài tập tự rèn luyện có đáp án chi tiết

Bài 1: Cho tam giác ABC trên trung tuyến AD lấy điểm I cố định. Đường thẳng d đi qua I lần lượt cắt cạnh AB, AC tại M, N. Tìm vị trí của đường thẳng d để diện tích tam giác AMN đạt giá trị nhỏ nhất.

Bài 2: Cho góc nhọn xOy và điểm I cố định nằm ở trong các góc đó. Đường thẳng d đi qua I và cắt Ox; Oy lần lượt tại M,N. Xác định đường thẳng d để diện tích tam giác OMN đạt giá trị nhỏ nhất.

Bài 3: Cho ba điểm A; I; B thẳng hàng theo thứ tự. Gọi $d_{1},d_{2}$ là hai nửa đường thẳng vuông góc với AB tại A; B và nằm về cùng một phía đối với đường thẳng AB. Góc vuông $\widehat{xIy}$ quay xung quanh đỉnh I sao cho hai cạnh của góc tương ứng cắt $d_{1}$ ở M, cắt $d_{2}$ ở N. Tìm vị trí của M, N để diện tích tam giác IMN đạt giá trị nhỏ nhất.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

----------------------------------------

Dạng toán tìm vị trí điểm M để tam giác có diện tích lớn nhất hoặc nhỏ nhất là một trong những chuyên đề quan trọng của hình học Toán lớp 9. Thông qua việc phân tích mối quan hệ giữa đáy và chiều cao của tam giác, học sinh có thể xác định được vị trí thích hợp của điểm M để đạt giá trị diện tích cực trị.

Để giải tốt dạng toán này, học sinh cần nắm chắc các kiến thức cơ bản về diện tích tam giác, đường vuông góc, khoảng cách từ điểm đến đường thẳng, đồng thời rèn luyện kỹ năng phân tích hình vẽ và lập luận hình học chặt chẽ. Khi luyện tập nhiều bài toán cùng dạng, học sinh sẽ dễ dàng nhận ra các phương pháp giải quen thuộc và áp dụng linh hoạt trong các bài thi.

Hy vọng rằng chuyên đề tìm vị trí điểm M để tam giác có diện tích lớn nhất, nhỏ nhất sẽ giúp các bạn củng cố kiến thức và nâng cao khả năng giải bài tập Toán 9. Đây cũng là tài liệu hữu ích trong quá trình ôn thi vào lớp 10 môn Toán, giúp học sinh tự tin hơn khi gặp các bài toán cực trị trong hình học.

Tải về

Chọn file muốn tải về: