Tổng hợp bài tập hình học ôn thi vào 10 có đáp án – Bộ đề trọng tâm giải chi tiết

Hình học 9 là phần kiến thức quan trọng và chiếm tỷ trọng lớn trong đề thi tuyển sinh vào lớp 10. Các dạng bài như đường tròn, tam giác, hệ thức lượng, góc – cung – dây, tiếp tuyến đều đòi hỏi học sinh nắm chắc lý thuyết và biết vận dụng linh hoạt vào từng bài tập. Bài viết này tổng hợp đầy đủ bài tập hình học trọng tâm ôn thi vào 10, kèm đáp án và lời giải chi tiết, giúp bạn luyện tập theo đúng cấu trúc đề thi, tránh các lỗi sai thường gặp và nâng cao khả năng tư duy hình học.

Phần I. Đề bài các bài tập hình học luyện thi vào lớp 10

Bài tập 1. Cho nửa đường tròn \((O)\), đường kính \(AB\). Từ điểm \(M\) bất kì trên tiếp tuyến \(Ax\) của nửa đường tròn \((O)\) vẽ tiếp tuyến thứ hai \(MC\) (\(C\) là tiếp điểm). Gọi \(I\)là giao điểm của \(OM\) và \(AC\).

a) Chứng minh bốn điểm \(A\), \(M\), \(C\), \(O\) cùng thuộc một đường tròn.

b) Chứng minh \(OI.OM = OA^{2}\) và \(OM\ //\ BC\).

c) Gọi \(H\) là chân đường vuông góc kẻ từ \(C\) đến \(AB\), \(MB\) cắt đường tròn \((O)\) tại \(D\) và cắt \(CH\) tại \(K\). Chứng minh \(K\) là trung điểm của \(CH\).

Bài tập 2. Cho tứ giác ABCD có AB nhỏ hơn AD; BC nhỏ hơn CD nội tiếp đường tròn đường kính BD, AB cắt DC tại E; CB cắt DA tại F, DB cắt EF tại G.

a) Chứng minh rằng \(BD\bot EF\) tại G

b) Chứng minh bốn điểm F, G, B, A cùng thuộc một đường tròn.

c) Chứng minh rằng \(BA.BE = BC.BF = BD.BG\)

d) Chứng minh rằng B là tâm đường tròn nội tiếp \(\Delta ACG\).

Bài tập 3. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H.

a) Chứng minh bốn điểm A, B, D, E cùng thuộc một đường tròn.

b) Chứng minh \(DB.DC = DH.DA\).

c) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.

d) Tính \(\frac{AH}{AD} + \frac{BH}{BE} + \frac{CH}{CF}\).

Bài tập 4. Cho tam giác \(ABC\) có ba góc đều nhọn. Các đường cao \(AK\), \(BE\) và \(CF\) cắt nhau tại \(H\). Gọi \(I\) là trung điểm của đoạn \(AH\), \(N\) là trung điểm của đoạn \(BC\)

a) Chứng minh bốn điểm \(A\), \(E\), \(H\), \(F\) nằm trên cùng một đường tròn.

b) Chứng minh \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\).

c) Chứng minh \(CI^{2} - IE^{2} = CK.CB\).

Bài tập 5. Cho đường tròn \((O)\) và dây cung \(AB\). Trên tia đối của tia \(AB\)lấy điểm C. Từ điểm chính giữa \(P\) của cung lớn \(AB\) kẻ đường kính \(PQ\) của đường tròn (O) cắt dây \(AB\) tại \(D\). Tia \(CP\) cắt đường tròn \((O)\) tại điểm \(I\)( điểm \(I\) khác điểm \(P\)). Các dây \(AB\) và \(QI\) cắt nhau tại \(K\)

a) Chứng minh tứ giác \(PDKI\) nội tiếp

b) Chứng minh rằng \(CI.CP = CK.CD\) và \(IC\) là phân giác góc ngoài tại đỉnh \(I\) của tam giác \(AIB\) .

c) Giả sử ba điểm\(A;B;C\) cố định. Chứng minh khi đường tròn \((O)\) thay đổi nhưng vẫn đi qua hai điểm\(A\) và \(B\) thì đường thẳng \(QI\) luôn đi qua một điểm cố định.

Bài tập 6. Cho đường tròn \((O)\), từ điểm \(A\)ở ngoài đường tròn vẽ hai tiếp tuyến \(AB\)và\(AC\)(\(B,\ \ C\)là các tiếp điểm), \(OA\) cắt \(BC\) tại E.

a) Chứng minh tứ giác \(ABOC\) nội tiếp.

b) Chứng minh \(BC\) vuông góc với \(OA\) và \(BA.BE = AE.BO\).

c) Gọi \(I\) thuộc đoạn thẳng \(BE\), đường thẳng qua \(I\)và vuông góc \(OI\) cắt các tia \(AB,\ \ AC\) theo thứ tự tại \(D\) và \(F\). Chứng minh \(F\) là trung điểm của\(AC\).

Bài tập 7. Cho tam giác \(ABC\) nhọn nội tiếp đường trong \((O)\), các đường cao \(AD,\ BE,CF\) cắt nhau tại \(H\). Kẻ đường kính \(AQ\) của đường tròn \((O)\) cắt cạnh \(BC\) tại \(I.\)

1) Chứng minh bốn điểm \(A,F,H,E\) cùng thuộc một đường tròn.

2) Gọi \(P\) là giao điểm của \(AH\) và \(EF\). Chứng minh \(\widehat{BAD}\) = \(\widehat{CAQ}\)

3) Chứng minh rằng: \(\Delta AEP\)∽\(\Delta ABI\) và \(PI//HQ\)

Bài tập 8. Cho tam giác \(ABC\) có ba góc nhọn nội tiếp đường tròn tâm \(O\) bán kính \(R\) và \(AH\) là đường cao của tam giác \(ABC\). Gọi \(M,\ N\) lần lượt là chân đường vuông góc kẻ từ \(H\) đến \(AB\) và \(AC\).

a) Chứng minh bốn điểm \(A,\ M,\ H,\ N\) cùng thuộc một đường tròn.

b) Chứng minh \(\widehat{ABC} = \widehat{ANM}\) và \(OA\) vuông góc với \(MN\).

c) Cho biết\(\ AH = R\sqrt{2}\). Chứng minh \(M,\ O,\ N\) thẳng hàng.

Bài tập 9. Cho đường tròn \((O;R)\) và dây \(BC\) cố định không đi qua tâm. Gọi \(A\) là một điểm bất kì trên cung lớn \(BC\) sao cho tam giác \(ABC\) nhọn \((AB < AC)\). Kẻ các đường cao \(AD,BE\) của tam giác \(ABC\).

a) Chứng minh: Bốn điểm \(A,E,D,B\) cùng nằm trên một đường tròn.

b) Kẻ đường kính \(AK\) của đường tròn tâm \(O\). Gọi F là hình chiếu của điểm \(B\) trên \(AK\). Chứng minh rằng: \(AB.AC = AK.AD\) và \(DF\bot AC\)

c) Gọi \(M\) là trung điểm của \(BC\). Chứng minh: ba điểm \(E;F;M\) thẳng hàng.

Bài tập 10. Cho tam giác \(ABC\) nhọn \((AB < AC)\) có đường cao \(AD\) và đường phân giác trong \(AO\) (\(D,\ O\) thuộc cạnh \(BC\)). Kẻ \(OM\) vuông góc với \(AB\) tại \(M\), \(ON\) vuông góc với \(AC\)tại \(N\).

a) Chứng minh: Tứ giác \(AMON\) nội tiếp

b) Chứng minh \(\widehat{BDM} = \widehat{ODN}\)

c) \(Sin\frac{BAC}{2} \leq \frac{BC}{AB + AC}\).

(Còn tiếp)

Phần II. Đáp án bài tập ôn luyện

Bài tập 1.

Hình vẽ minh họa:

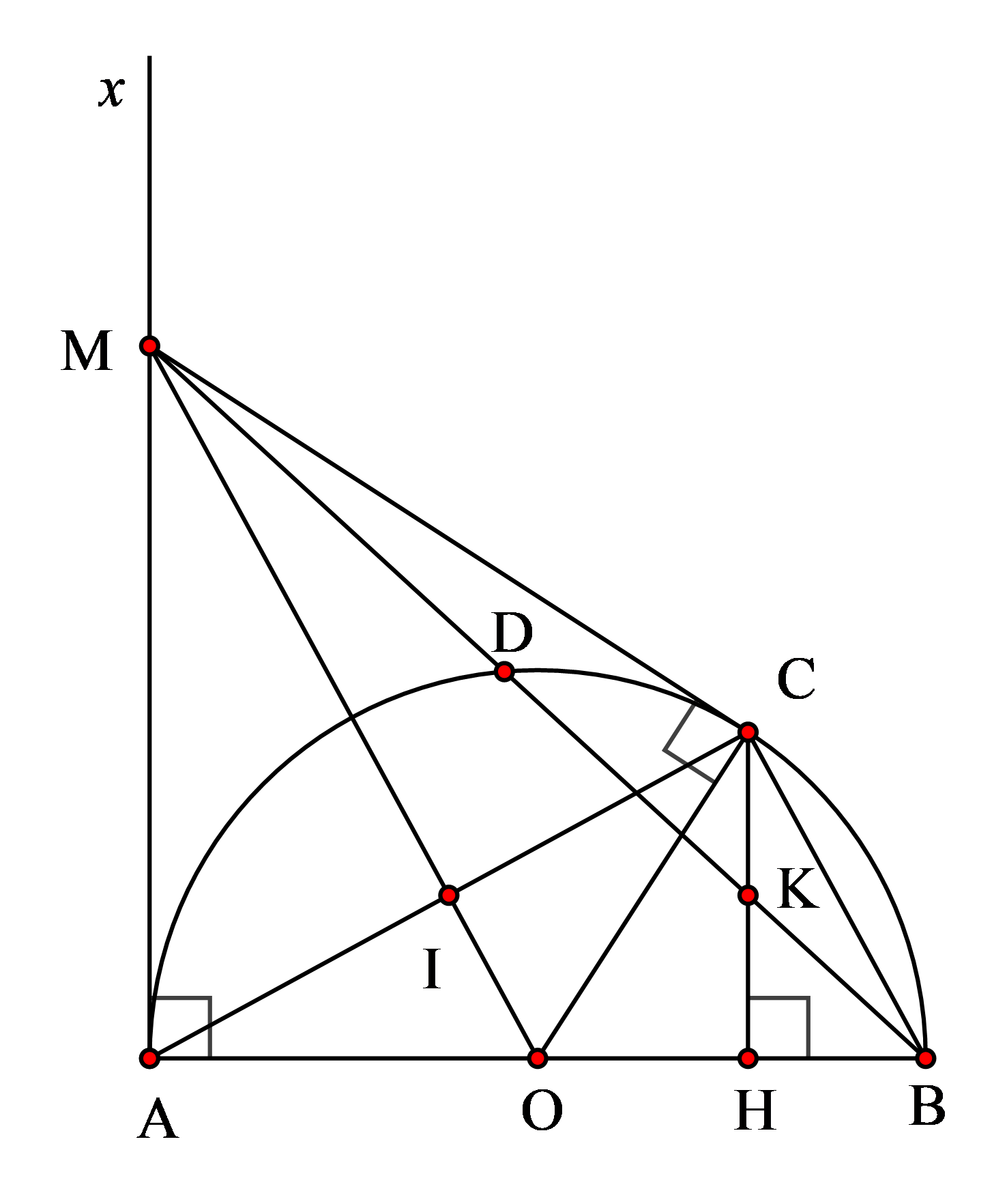
a) Chứng minh bốn điểm \(A\), \(M\), \(C\), \(O\) cùng thuộc một đường tròn.

Xét đường tròn \((O)\),

+ Do \(AM\) là tiếp tuyến của \((O)\) nên \(MA\bot OA\). Suy ra \(\widehat{MAO} = 90^{0}\).

Suy ra \(A\) thuộc đường tròn đường kính \(MO\) (1)

+ Do \(MC\) là tiếp tuyến của \((O)\)nên \(MC\bot OC\). Suy ra \(\widehat{MCO} = 90^{0}\).

Suy ra \(C\) thuộc đường tròn đường kính \(MO\) (2)

Từ (1) và (2) suy ra 4 điểm \(A\), \(M\), \(C\), \(O\)cùng thuộc một đường tròn (đpcm)

b) Chứng minh \(OI.OM = OA^{2}\) và \(OM\ //\ BC\).

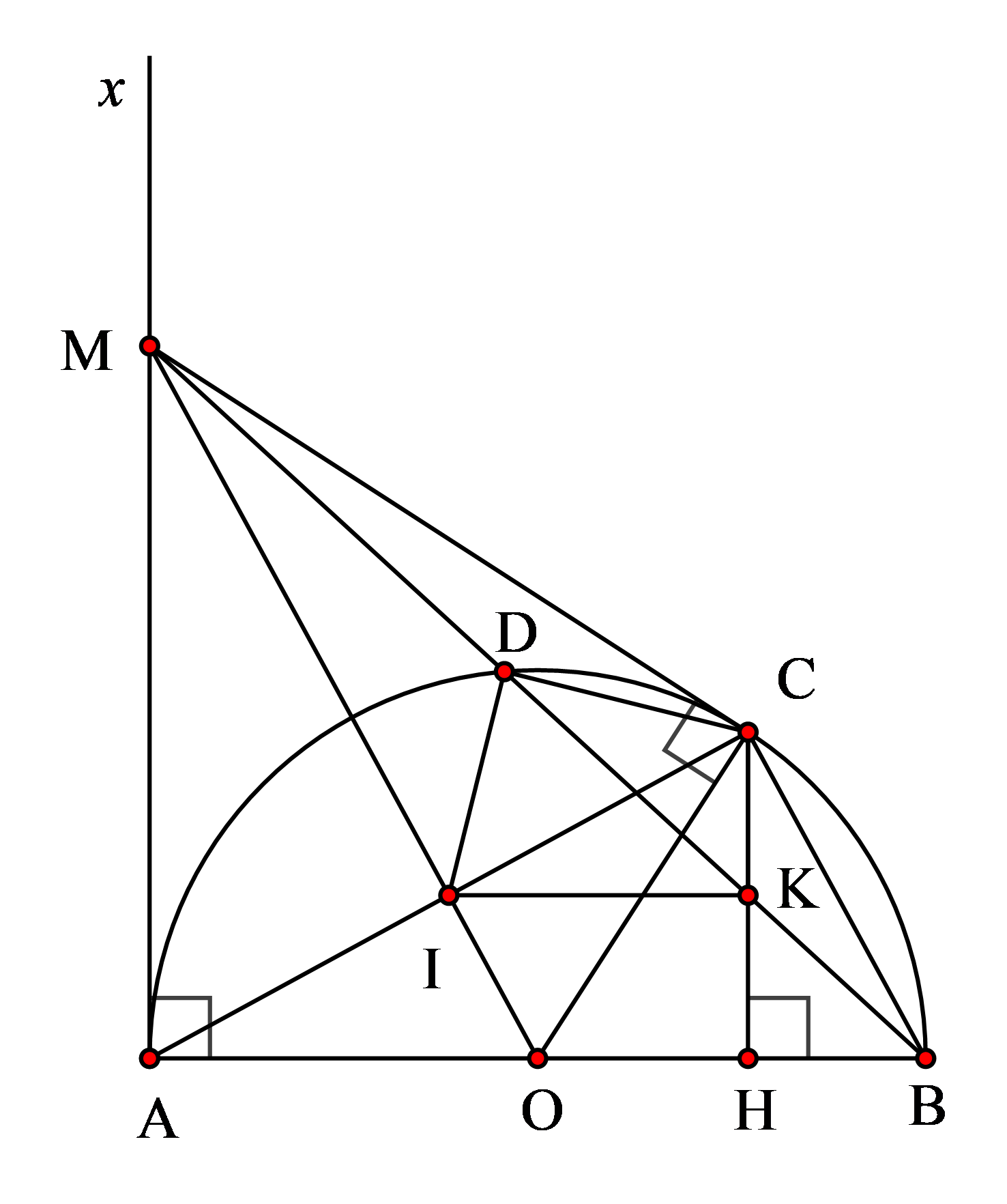
Xét đường tròn \((O)\) có hai tiếp tuyến \(MA\), \(MC\) cắt nhau tại \(M\) suy ra \(MA = MC\)

Mà \(OA = OC = R\)

Suy ra \(OM\) là đường trung trực của \(AC\).

Suy ra \(OM\bot AC\ \ \ (3)\). Mà \(I \in AC\) nên \(AI\bot OM\).

Xét \(\Delta OIA\) và \(\Delta OAM\) có:

\(\left. \ \begin{matrix} \widehat{OIA} = \widehat{OAM} = 90^{0} \\ \widehat{AOM}\ \ chung \end{matrix} \right\} \Rightarrow \Delta OAI\mathbf{\backsim}\Delta OAM\) (g - g)

Suy ra \(\frac{OI}{OA} = \frac{OA}{OM}\) hay \(OI.OM = OA^{2}\)(điều phải chứng minh)

Ta có \(\widehat{ACB} = 90^{0}\) (góc nội tiếp chắn nửa đường tròn)

\(\Rightarrow AC\bot BC\)  (4)

Từ (3) và (4) \(\Rightarrow OM\ //\ BC\) (điều phải chứng minh)

c) Chứng minh \(K\) là trung điểm của \(CH\).

Do \(CH\ //\ AM\) (cùng vuông góc với \(AB\)).

\(\widehat{HCA} = \widehat{CAM}\) (hai góc so le trong) (5)

Mà \(MA = MC\) (cmt) nên \(\Delta MAC\) cân tại \(M\).

\(\Rightarrow \widehat{MAC} = \widehat{MCA}\) (tính chất tam giác cân) (6)

Từ (5) và (6) suy ra \(\widehat{MCA} = \widehat{HCA}\).

Suy ra \(AC\) là tia phân giác \(\widehat{MCH}\).

Mà \(AC\bot CB(cmt)\)

Suy ra \(CB\)là phân giác ngoài tại \(C\) của \(\Delta KCM \Rightarrow \frac{BK}{BM} = \frac{CK}{CM}(7)\)

Xét \(\Delta ABM\) có \(KH\ //\ AM\) (cùng vuông góc với \(AB\))

Suy ra \(\frac{BK}{BM} = \frac{KH}{AM}\ \ \ \ (8)\)

Từ (7) và (8) suy ra \(\frac{CK}{CM} = \frac{KH}{AM}\).

Mà \(CM = AM(cmt)\) nên \(CK = KH\).

Vậy \(K\) là trung điểm của \(CH\) (điều phải chứng minh)

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

----------------------------------------------

Bộ bài tập hình học ôn thi vào 10 được tổng hợp ở trên không chỉ giúp bạn củng cố kiến thức nền tảng mà còn rèn kỹ năng giải bài một cách chắc chắn và khoa học. Hãy luyện tập đều đặn, phân tích từng dạng bài và áp dụng đúng phương pháp để nâng cao hiệu quả ôn thi. Chúc bạn tự tin đạt điểm cao trong kỳ thi tuyển sinh lớp 10 và chinh phục các bài hình học khó một cách nhẹ nhàng.