Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Bài toán tương giao đồ thị hàm số bậc nhất với bậc nhất

Chuyên đề Toán 9 ôn thi vào 10

Bài trước

Bài sau

Lớp: Lớp 9

Môn: Toán

Mức độ: Trung bình

Phân loại: Tài liệu Tính phí

Cách giải bài toán tương giao đồ thị bậc nhất

Trong chương trình Toán 9, dạng bài tương giao đồ thị hàm số bậc nhất với bậc nhất là một chủ đề quan trọng, thường xuyên xuất hiện trong đề thi vào lớp 10. Nắm vững phương pháp giải không chỉ giúp học sinh hiểu rõ hơn về hàm số bậc nhất mà còn rèn luyện kỹ năng vẽ và phân tích đồ thị. Bài viết này sẽ hướng dẫn chi tiết cách nhận biết, phương pháp giải và đưa ra ví dụ minh họa cụ thể, giúp bạn học chắc và làm bài hiệu quả.

Bài tập 1. Cho các hàm số bậc nhất: y = 0,5x + 3; y = 6 - x và y = mx có đồ thị lần lượt là các đường thẳng (d₁), (d₂) và (∆_m). Với những giá trị nào của tham số m thì đường thẳng (∆_m) cắt hai đường thẳng (d₁) và (d₂) lần lượt tại hai điểm A và B sao cho điểm A có hoành độ âm còn điểm B có hoành độ dương?

Hướng dẫn giải

Điều kiện để (∆_m) là đồ thị hàm số bậc nhất là m ≠ 0

Phương trình hoành độ giao điểm của (d₁) và (∆_m) là:

0,5x + 3 = mx ⇔ (m - 0,5)x = 3

Điều kiên để phương trình này có nghiệm âm là m - 0,5 < 0 hay m < 0,5

Phương trình hoành độ giao điểm của (d₂) và (∆_m) là:

6 - x = mx ⇔ (m + 1)x = 6

Điều kiên để phương trình này có nghiệm dương là m + 1 > 0 hay m > -1

Vậy điều kiện cần tìm là: $- 1 < m < 0,5;m \neq 0$ .

Bài tập 2. Trong mặt phẳng tọa độ Oxy, gọi (D) và (L) lần lượt là đồ thị của hai hàm số: $y = - \frac{1}{2}x + \frac{3}{2}$ và .

a) Vẽ đồ thị (D) và (L).

b) (D) và (L) cắt nhau tại M và N. Chứng minh OMN là tam giác vuông.

Hướng dẫn giải

Đồ thị $y = - \frac{1}{2}x + \frac{3}{2}$ có: $\left\{ \begin{matrix} x = 0 \Rightarrow y = \frac{3}{2} \\ y = 0 \Rightarrow x = 3 \end{matrix} \right.$

Đồ thị $y = |x| = \left\{ \begin{matrix} x\ khi\ x \geq 0 \\ - x\ khi\ x \leq 0 \end{matrix} \right.$

Đồ thị như hình vẽ:

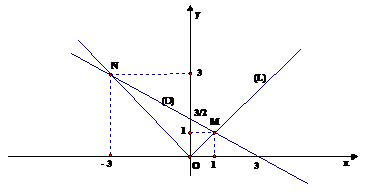
Đồ thị (D) và (L) cắt nhau tại hai điểm có tọa độ M(1; 1) và N( - 3; 3)

Ta có: OM = $\sqrt{1^{2} + 1^{2}} = \sqrt{2} \Rightarrow$ OM² = 2

ON = $\sqrt{3^{2} + ( - 3)^{2}} = 3\sqrt{2} \Rightarrow$ ON² = 18

MN = $\sqrt{(1 - 3)^{2} + (1 + 3)^{2}} = \sqrt{20} \Rightarrow$ MN² = 20

Vì: OM² + ON² = MN²

Vậy: tam giác OMN vuông tại O.

Bài tập 3. Cho hai đường thẳng d₁ và d₂ lần lượt có phương trình y = -2x + 4 và y = 2x - 2

a) Tìm tọa độ giao điểm A của hai đường thẳng trên.

b) Vẽ trên cùng một hệ trục tọa độ các đường thẳng d₁ và d₂

c) Gọi B và C lần lượt là giao điểm của d₁ và d₂ với trục hoành; D và E lần lượt là giao điểm của d₁ và d₂ với trục tung. Tính diện tích các tam giác ABC, ADE, ABE.

d) Tính các góc tạo bởi đường thẳng d₁ và d₂ với trục hoành.

Hướng dẫn giải

a) Giao điểm của hai đường thẳng là nghiệm của hệ phương trình sau:

$\left\{ \begin{matrix} y = - 2x + 4 \\ y = 2x - 2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{4 - y}{2} \\ 2y = 2 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{3}{2} \\ y = 1 \end{matrix} \right.$

Vậy giao điểm A của hai đường thẳng là $A\left( \frac{3}{2};1 \right)$

b) Xét đường thẳng (d₁): y = -2x + 4

Với x = 0=> y = 4 ; y = 0 => x = 2. Đường thẳng (d₁) đi qua hai điểm (0 ; 4) và (2; 0)

Xét đường thẳng (d₂) : y = 2x - 2

Với x = 0 => y = -2 ; y = 0 => x = 1. Đường thẳng (d₁) đi qua hai điểm (0 ; -2) và (1; 0)

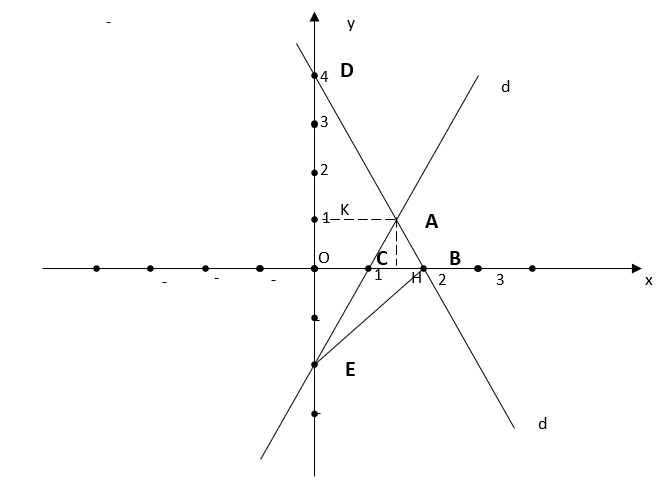
c) Ta có: $A\left( \frac{3}{2};1 \right)$ , B(2; 0), C(1; 0), D(0; 4) và E(0; -2)

Do đó: BC = | 2 – 1| = 1 , DE = | 4 - (-2)| = 6 , BO = | 2 – 0 | = 2

Gọi AH là đường cao của $\Delta$ ABC , AK là đường cao của $\Delta$ ADE => AH = 1 , AK = $\frac{3}{2}$

Gọi $S_{ABC};S_{ADE};S_{BDE};S_{ABE}$ lần lượt là diện tích của các tam giác ABC , ADE , BDE , ABE.

Ta có :

$S_{ABC} = \frac{1}{2}AH.BC = \frac{1}{2}.1.1 = \frac{1}{2}$ (đơn vị diện tích)

$S_{ADE} = \frac{1}{2}AK.DE = \frac{1}{2}.\frac{3}{2}.6 = \frac{9}{2}$ (đơn vị diện tích)

$S_{BDE} = \frac{1}{2}BO.DE = \frac{1}{2}.2.6 = 6$ (đơn vị diện tích)

$S_{ABE} = S_{BDE} - S_{ADE} = \frac{3}{2}$ (đơn vị diện tích)

d) Góc tạo bởi đường thẳng d₁ và d₂ với trục hoành lần lượt là $\widehat{DBx};\widehat{ACx}$

Tam giác OBD vuông tại O có: $\tan\widehat{OBD} = \frac{OD}{OB} = 2 \Rightarrow \widehat{OBD} = 63^{0}4'$

$\Rightarrow \widehat{BDx} = 180^{0} - 63^{0}4' = 116,6^{0}$

Tam giác OCE vuông tại O có: $\tan\widehat{OCE} = \frac{OE}{OC} = 2 \Rightarrow \widehat{OCE} = 63^{0}4'$

$\Rightarrow \widehat{ACx} = 63^{0}4'$

Vậy góc tạo bởi đường thẳng d₁ và d₂ với trục hoành cùng là 63,4⁰.

Bài tập 4. Cho hàm số bậc nhất : y = (2m – 5)x + 3 với $m \neq \frac{5}{2}$ có đồ thị là đường thẳng d. Tìm giá trị của m để:

a. Góc tạo bởi (d) và và trục Ox là góc nhọn, góc tù ( hoặc hàm số đồng biến, nghịch biến)

b. (d) đi qua điểm (2 ; -1)

c. (d) song song với đường thẳng y = 3x – 4

d. (d) song song với đường thẳng 3x + 2y = 1

e. (d) luôn cắt đường thẳng 2x – 4y – 3 = 0

f. (d) cắt đường thẳng 2x + y = -3 tại điểm có hoành độ là -2

g. (d) cắt trục hoành tại điểm ở bên trái trục tung (có hoành độ âm)

h. (d) cắt đường thẳng y = 3x + 1 tại điểm có hoành độ âm (hoặc ở bên trái trục tung)

i. (d) cắt đường thẳng y = 5x – 3 tại điểm có tung độ dương (hoặc ở trên trục hoành)

k. Chứng tỏ (d) luôn đi qua một điểm cố định trên trục tung

Hướng dẫn giải

Hàm số có a = 2m – 5 ; b = 3

a. Góc tạo bởi đường thẳng d và và trục Ox là góc nhọn, góc tù

Góc tạo bởi đường thẳng d và và trục Ox là góc nhọn khi đường thẳng d có hệ số a > 0 $\Leftrightarrow$ 2m – 5 >0 $\Leftrightarrow$ $m > \frac{5}{2}$ (thỏa mãn)

Góc tạo bởi đường thẳng d và và trục Ox là góc tù khi đường thẳng d có hệ số a < 0 $\Leftrightarrow$ 2m – 5 <0 $\Leftrightarrow$ $m < \frac{5}{2}$ (thỏa mãn)

Vậy góc tạo bởi đường thẳng d và và trục Ox là góc nhọn khi $m > \frac{5}{2}$

Góc tạo bởi đường thẳng d và và trục Ox là góc tù khi $m < \frac{5}{2}$

b. (d) đi qua điểm (2 ; -1)

Thay x = 2 ; y = -1 vào phương trình đường thẳng d ta có

-1 = 2. (2m - 5) + 3 $\Leftrightarrow$ 4m – 10 + 3 = -1 $\Leftrightarrow$ $m = \frac{3}{2}$ (thỏa mãn)

Vậy với $m = \frac{3}{2}$ thì (d) đi qua điểm (2 ; -1)

Chú ý: Phải viết là “Thay x = 2 ; y = -1 vào phương trình đường thẳng d ”, không được viết là “Thay x = 2 ; y = -1 vào đường thẳng d ”

c. (d) song song với đường thẳng y = 3x - 4

(d) song song với đường thẳng y = 3x - 4 $\Leftrightarrow \left\{ \begin{matrix} 2m - 5 = 3 \\ 3 \neq - 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m = 4 \\ 3 \neq - 4 \end{matrix} \right.\ \Leftrightarrow m = 4$ (thỏa mãn)

Vậy m = 4 là giá trị cần tìm

d. (d) song song với đường thẳng 3x + 2y = 1

Ta có 3x + 2y = 1 $\Leftrightarrow$ $y = - \frac{3}{2}x + \frac{1}{2}$

(d) song song với đường thẳng 3x + 2y = 1 $\Leftrightarrow$ (d) song song với đường thẳng $y = - \frac{3}{2}x + \frac{1}{2}$

$\Leftrightarrow \left\{ \begin{matrix} 2m - 5 = - \frac{3}{1} \\ 3 \neq \frac{1}{2} \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} m = \frac{7}{4} \\ 3 \neq \frac{1}{2} \end{matrix} \right.\ \Leftrightarrow m = \frac{7}{4}$ (thỏa mãn) .

Vậy $m = \frac{7}{4}$ là giá trị cần tìm

e. (d) luôn cắt đường thẳng 2x - 4y - 3 = 0

Ta có 2x - 4y - 3 = 0 $\Leftrightarrow y = \frac{1}{2}x - \frac{3}{4}$

(d) luôn cắt đường thẳng 2x - 4y - 3 = 0 $\Leftrightarrow$ (d) luôn cắt đường thẳng $y = \frac{1}{2}x - \frac{3}{4}$ $\Leftrightarrow 2m - 5 \neq \frac{1}{2} \Leftrightarrow m \neq \frac{11}{4}$ .

Kết hợp với điều kiên ta có: $m \neq \frac{5}{2};m \neq \frac{11}{4}$ là giá trị cần tìm.

f. (d) cắt đường thẳng 2x + y = -3 tại điểm có hoành độ là -2

Thay x = -2 vào phương trình đường thẳng 2x + y = -3 ta được 2. (-2) + y = -3 $\Leftrightarrow$ y = 1

=> (d) cắt đường thẳng 2x + y = -3 tại điểm (-2 ; 1).

Thay x = -2 ; y = 1 vào phương trình đường thẳng d ta có 1 = ( 2m – 5 ). (-2) + 3 $\Leftrightarrow$ -4m + 10 +3 = 1 $\Leftrightarrow$ m = 3 (thỏa mãn).

Vậy m = 3 là giá trị cần tìm.

g. (d) cắt trục hoành tại điểm ở bên trái trục tung ( có hoành độ âm)

Thay y = 0 vào phương trình đường thẳng d ta có 0 = (2m - 5)x + 3 $\Leftrightarrow x = \frac{- 3}{2m - 5}$

(d) cắt trục hoành tại điểm ở bên trái trục tung $\Leftrightarrow \frac{- 3}{2m - 5} < 0 \Leftrightarrow 2m - 5 > 0 \Leftrightarrow m > \frac{5}{2}$ (thỏa mãn).

Vậy $m > \frac{5}{2}$ là giá trị cần tìm.

h. (d) cắt đường thẳng y = 3x + 1 tại điểm có hoành độ âm (hoặc ở bên trái trục tung)

(d) cắt đường thẳng y = 3x + 1 $\Leftrightarrow$ 2m – 5 $\neq$ 3 $\Leftrightarrow$ m $\neq$ 4

Hoành độ giao điểm của (d) và đường thẳng y = 3x + 1 là nghiệm của phương trình ẩn x sau :

( 2m – 5 )x + 3 = 3x + 1 $\Leftrightarrow$ ( 2m - 8)x = -2 $\Leftrightarrow x = - \frac{2}{2m - 8}$ ( vì m $\neq$ 4 )

(d) cắt đường thẳng y = 3x + 1 tại điểm có hoành độ âm

$\Leftrightarrow - \frac{2}{2m - 8} < 0 \Leftrightarrow 2m - 8 > 0 \Leftrightarrow m > 4$ (thỏa mãn các điều kiện $m \neq \frac{5}{2}$ và m $\neq$ 4 )

Vậy m > 4 là giá trị cần tìm.

i. (d) cắt đường thẳng y = 5x - 3 tại điểm có tung độ dương ( hoặc ở trên trục hoành)

* (d) cắt đường thẳng y = 5x - 3 $\Leftrightarrow$ 2m – 5 $\neq$ 5 $\Leftrightarrow$ m $\neq$ 5

* Hoành độ giao điểm của (d) và đường thẳng y = 5x - 3 là nghiệm của phương trình ẩn x sau :

( 2m – 5 )x + 3 = 5x - 3 $\Leftrightarrow$ (2m - 10)x = -6 $\Leftrightarrow x = \frac{- 6}{2m - 10} = \frac{- 3}{m - 5}$ ( vì m $\neq$ 5 )

Thay $x = \frac{- 3}{m - 5}$ vào phương trình đường thẳng y = 5x - 3 ta có:

y = $5.\frac{- 3}{m - 5} - 3 = \frac{- 15 - 3m + 15}{m - 5} = \frac{- 3m}{m - 5}$

(d) cắt đường thẳng y = 5x - 3 tại điểm có tung độ dương

$\Leftrightarrow \frac{- 3m}{m - 5} > 0 \Leftrightarrow - 3m.(m - 5) > 0 \Leftrightarrow m(m - 5) < 0 \Leftrightarrow 0 < m < 5$

Kết hợp với các điều kiện ta có 0 < m < 5 và $m \neq \frac{5}{2}$ là giá trị cần tìm

k. Chứng tỏ (d ) luôn đi qua một điểm cố định trên trục tung

Giả sử (d) luôn đi qua điểm cố định có tọa độ ( x₀ ; y₀). Khi đó :

y₀ = ( 2m – 5 )x₀ + 3 với mọi m $\Leftrightarrow$ 2x₀m – 5x₀ – y₀ + 3 = 0 với mọi m

$\Leftrightarrow \left\{ \begin{matrix} 2x_{0} = 0 \\ - 5x_{0} - y_{0} + 3 = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{0} = 0 \\ y_{0} = 3 \end{matrix} \right.$

Vậy (d) luôn đi qua một điểm cố định trên trục tung có tọa độ là (0 ; 3).

-------------------------------------------------------

Qua chuyên đề tương giao đồ thị hàm số bậc nhất với bậc nhất, học sinh có thể hệ thống lại kiến thức về hàm số bậc nhất, kỹ năng lập phương trình đường thẳng và cách tìm tọa độ giao điểm. Đây là kiến thức nền tảng để tự tin bước vào kỳ thi tuyển sinh lớp 10. Để đạt kết quả cao, bạn nên kết hợp việc luyện tập nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao. Hy vọng bài viết đã mang lại cho bạn tài liệu hữu ích trong hành trình ôn thi Toán 9 vào 10.

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Ma Kết

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Đấu Trường Tri Thức

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bài toán tương giao đồ thị hàm số bậc nhất với bậc nhất

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Cách giải bài toán tương giao đồ thị bậc nhất

Có thể bạn quan tâm

Bộ chuyên đề Toán 9 ôn thi vào lớp 10 đầy đủ các dạng bài

Chuyên đề Toán 9 Kết nối tri thức

Chuyên đề Toán 9 Chân trời sáng tạo

Chuyên đề Toán 9 ôn thi vào 10