Bài tập về các góc trong đường tròn (Có đáp án)

Bài tập về các góc trong đường tròn được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 hiệu quả hơn. Mời các bạn tham khảo.

• Chuyên đề Phương trình bậc hai chứa tham số Toán 9 (Có đáp án)
• Chuyên đề Tứ giác nội tiếp Toán 9 (Có đáp án)
• Các bài toán về tiếp tuyến và cát tuyến (Có đáp án)

Đây là phần bài tập về Các loại góc trong đường tròn Toán lớp 9 được chia làm ba phần: Lý thuyết, bài tập trắc nghiệm và tự luận, đáp án. Phần đầu tiên sẽ tổng hợp lại kiến thức về các loại góc có trong đường tròn bao gồm: góc ở tâm, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung, góc có đỉnh nằm bên trong đường tròn và góc có đỉnh nằm bên ngoài đường tròn. Phần bài tập được sưu tầm và chọn lọc để các bạn học sinh có thể áp dụng lý thuyết phía trên để làm bài. Qua đó sẽ giúp cho các bạn học sinh ôn tập và củng cố lại kiến thức về phần góc trong đường tròn nói riêng và Hình học lớp 9 nói chung để chuẩn bị cho kì thi tuyển sinh vào lớp 10.

I. Các dạng bài tập về góc trong đường tròn

A. Góc ở tâm

Câu 1. Hai tiếp tuyến tại hai điểm A, B của đường tròn (O) cắt nhau tại M, tạo thành góc AMB bằng 50⁰. Số đo của góc ở tâm chắn cung AB là:

A. 50⁰ . B. 40⁰ . C. 130⁰. D. 310⁰.

Câu 2. Cho (O; 4 cm), vẽ cung MN có số đo 60⁰ thì độ dài NM bằng:

A. 2 cm. B. 4 cm. C. 4 cm. D. 4 cm.

Câu 3. Cho (O; 2 cm), vẽ cung MN có số đo 90⁰ thì độ dài NM bằng:

A. 2 cm. B. 3 cm. C. 2 cm. D. 2 cm.

Câu 4. Cho (O; 3 cm), vẽ cung MN có số đo 120⁰ thì độ dài NM bằng:

A. 2 cm. B. 3 cm. C. 3 cm. D. 3 cm.

Câu 5. Cho (O; R cm), vẽ cung MN có số đo 120⁰ biết NM = 5 cm thì độ dài R bằng:

A. 2 cm. B. 5 cm. C. cm. D. 5 cm.

Câu 6. Cho (O; R cm), vẽ cung AB có số đo 90⁰ biết AB = 2 cm thì độ dài R bằng:

A. 2 cm. B. 5 cm. C. cm. D. cm.

Câu 7. Tam giác ABC đều nội tiếp đường tròn (O) thì số đo cung nhỏ BC bằng:

A. 60⁰. B. 120⁰. C. 90⁰. D. 100⁰.

Câu 8. Cho đường tròn (O, R), từ A sao cho OA = 2R, vẽ các tiếp tuyến AB và AC thì số đo cung nhỏ BC bằng:

A. 120⁰. B. 60⁰. C. 90⁰. D. 100⁰.

Câu 9. Khẳng định nào sai?

A. Trong một đường tròn nếu hai cung bằng nhau thì số đo bằng nhau.

B. Trong một đường tròn nếu số đo cung nhỏ bằng 150⁰ thì số đo cung lớn có cùng hai đầu mút với cung nhỏ có số đo bằng 210⁰.

C. Trong một đường tròn nếu hai cung có số đo bằng nhau thì bằng nhau.

D. Trong đường tròn cung nào lớn hơn thì số đo lớn hơn.

Câu 10. Cho đường tròn (O,R) cho cung MN có số đo 200⁰ , thì góc ở tâm MÔN bằng

A. 160⁰. B. 200⁰. C. 180⁰. D. 100⁰.

B. Góc nội tiếp

Bài 1: Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B . Vẽ cát tuyến CAD vuông góc với AB. Tia CB cắt (O’) tại E, tia BD cắt (O) tại F. Chứng minh rằng:

a) ∠CAF = ∠DAE.

b) AB là tia phân giác của ∠EAF.

c) CA.CD = CB.CE.

d) CD² = CB.CE + BD.CF.

Bài 2: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh rằng:

a) MA.MB = MC.MD.

b) Tứ giác ABEC là hình thang cân.

c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Bài 3: Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM.

a) Chứng minh ΔACN = ΔBCM.

b) Chứng minh ΔCMN vuông cân.

c) Tứ giác ANCD là hình gì? Vì sao?

C. Góc tạo bởi tiếp tuyến và dây cung

Bài 1: Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA² = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).

Bài 2: Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với (O) tại A và B. Qua A vẽ đường thẳng song song với MB cắt đường tròn tại C. Nối C với M cắt đường tròn (O) tại D. Nối A với D cắt MB tại E. Chứng minh rằng:

a) ΔABE ∼ ΔBDE; ΔMEA ∼ ΔDEM.

b) E là trung điểm của MB.

Bài 3: Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đọan AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt lại E và F. Tiếp tuyến C với nửa đường tròn cắt EF tại M và cắt AB tại N.

a) Chứng minh M là trung điểm của EF.

b) Tìm vị trí của điểm C trên đường tròn (O) sao cho ΔACN cân tại C.

Bài 4: Cho nửa đường tròn (O) đường kính AB = 2R. Gọi M là một điểm thay đổi trên tiếp tuyến Bx của (O). Nối AM cắt (O) tại N. Gọi I là trung điểm của AN.

a) Chứng minh: ΔAIO ∼ ΔBMN; ΔOBM ∼ ΔINB.

b) Tìm vị trí của điểm M trên tia Bx để diện tích ΔAIO có giá trị lớn nhất.

Bài 5: Cho đường tròn (O; R) và dây AB, gọi I là trung điểm của dây AB. Trên tia dối của tia BA lấy điểm M. Kẻ hai tiếp tuyến MC, MD với đường tròn, (C, D ≠ (O)).

a) Chứng minh rằng: Năm điểm O, I, C, M, D cùng nằm trên một đường tròn.

b) Gọi N là giao điểm của tia OM với (O). Chứng minh rằng N là tâm đường tròn nội tiếp.

D. Góc có đỉnh nằm bên trong đường tròn và góc có đỉnh nằm bên ngoài đường tròn

Câu 1: Trong hình 1, Biết số đo cung LK bằng 100⁰ thì số đo góc C bằng:

A.30⁰. B. 40⁰. C. 45⁰. D. 50⁰

Câu 2: Trong hình 1 Biết số đo cung LK bằng 100⁰ thì số đo góc AMB bằng:

A.120⁰. B. 140⁰. C. 145⁰. D. 160⁰

Câu 3: Trong hình 2, cho đường tròn (O; R), dây cung LK = R thì số đo góc C bằng:

A.50⁰. B. 100⁰. C. 60⁰. D. 40⁰

Câu 4: Trong hình 2, cho đường tròn (O; R), dây cung LK = R thì số đo góc LMK bằng:

A.120⁰. B. 140⁰. C. 145⁰. D. 160⁰

Câu 5: Trong hình 3, biết sđ +sđ = 170⁰ thì số đo góc bằng:

A.120⁰. B. 140⁰. C. 145⁰. D. 95⁰

Câu 6: Trong hình 3, biết sđ - sđ = 62⁰ thì số đo góc  bằng:

A.20⁰. B. 40⁰. C. 31⁰. D. 62⁰

II. Đáp án bài tập góc thuộc đường tròn

1. Góc ở tâm

Câu	1	2	3	4	5	6	7	8	9	10
Đáp án	C	B	C	D	B	C	B	A	A	A

2. Góc nội tiếp

Bài 1:

Hình vẽ minh họa:

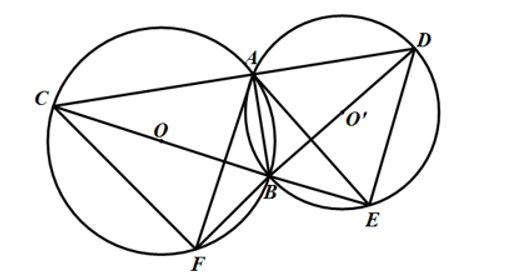
Vì CD ⊥ AB => ∠CAB = 90^o

Mà ∠CAB = 1/2 sđ => sđ = 180^o

Vậy ba điểm B, O, C thằng hàng.

Chứng minh tương tự ta có B, O’, D thẳng hàng.

a) Chứng minh ∠CAF = ∠DAE

Trong (O) ta có: ∠CAF = ∠CBF (góc nội tiếp cùng chắn cung CF )

Trong (O’) ta có: ∠DAE = ∠DBE (góc nội tiếp cùng chắn cung DE )

Mà ∠CBF = ∠DBE (đối đỉnh)

=> ∠CAF = ∠DAE.

b) AB là tia phân giác của ∠EAF

Nối CF và DE ta có: ∠CFB = 90^o (góc nội tiếp chắn nửa đường tròn (O))

∠BED = 90^o (góc nội tiếp chắn nửa đường tròn (O’))

Xét ΔCFB và ΔDEB có:

∠CFB = ∠BED = 90^o

∠CBF = ∠DBE (đối đỉnh)

=> ∠FCB = ∠EDB

Mặt khác: ∠FAB = ∠FCB (góc nội tiếp (O) cùng chắn cung FB)

∠EAB = ∠EDB (góc nội tiếp (O’) cùng chắn cung EB) s

=> ∠FAB = ∠EAB hay AB là phân giác của góc ∠EAF.

c) Chứng minh CA.CD = CB.CE

Xét ΔCAE và ΔCBD có:

∠C chung

∠CEA = ∠BDA (góc nội tiếp (O’) cùng chắn cung AB)

=> ΔCAE ∼ ΔCBD (g.g) => CA/CB = CE/CD hay CA.CD = CB.CE (1)

d) Chứng minh CD² = CB.CE + BD.CF

Chứng minh tương tự câu c) ta có: DA.DC = DB.DF (2)

Từ (1) và (2) suy ra:

CA.CD + DA.DC = CB.CE + DB.DF

⇔ (CA + DA)CD = CB.CE + DB.DF

⇔ CD² = CB.CE + DB.DF

Bài 2:

Hình vẽ minh họa:

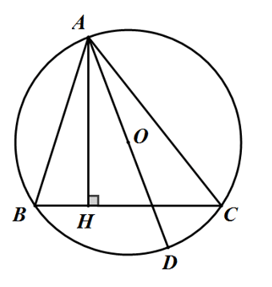
a) Chứng minh MA.MB = MC.MD.

Xét ΔAMC và ΔDMB có:

∠ACD = ∠ABD (góc nội tiếp cùng chắn cung AD)

∠AMC = ∠BMD = 90^o (gt)

=> ΔAMC ∼ ΔDMB (g.g)

=> MA/MD = MC/MB => MA.MB = MC.MD

b) Chứng minh tứ giác ABEC là hình thang cân.

Vì ∠DCE = 90^o (góc nội tiếp chắn nửa đường tròn)

=> CD ⊥ CE CD ⊥ AB (gt) => AB // CE.

=> Tứ giác ABEC là hình thang (1).

Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE

=> (2)

Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân.

c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Ta có (cmt) => EA = BC .

Mặt khác: ∠DAE = 90^o (góc nội tiếp chắn nửa đường tròn)

Do đó: MA² + MB² + MC² + MD² = (MA²+ MD²) + (MB² + MC²)

= AD² + BC² = DE² = 4R² không đổi

📚 Phần tiếp theo của tài liệu đã được tổng hợp trong file đính kèm, mời bạn tải về để đọc tiếp.

-----------------------------------------------------

Ngoài Bài tập về các góc trong đường tròn, để giúp bạn đọc có thêm nhiều tài liệu học tập hơn nữa, VnDoc.com mời các bạn học sinh tham khảo thêm đề thi học kì 2 môn Toán 9, đề cương ôn tập môn Toán 9 học kì 2 hay một số đề thi ôn thi vào lớp 10 như 40 Đề thi Toán vào lớp 10 chọn lọc, 21 Đề thi vào lớp 10 môn Toán,... mà chúng tôi đã sưu tầm và chọn lọc. Với các bài tập về các góc trong đường tròn này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!

Để giúp bạn đọc có thể giải đáp được những thắc mắc và trả lời được những câu hỏi khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt câu hỏi tại mục hỏi đáp học tập của VnDoc. Chúng tôi sẽ hỗ trợ trả lời giải đáp thắc mắc của các bạn trong thời gian sớm nhất nhé.