Các bài toán về tiếp tuyến và cát tuyến (Có đáp án)
Các bài toán về tiếp tuyến và cát tuyến
Các bài toán về tiếp tuyến và cát tuyến được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9 luyện thi vào lớp 10 hiệu quả hơn. Mời các bạn tham khảo.
Đây là phần bài tập về Tiếp tuyến và Cát tuyến Toán lớp 9 được chia làm hai phần: Lý thuyết và bài tập vận dụng. Phần đầu tiên sẽ tổng hợp lại kiến thức về Tiếp tuyến và Cát tuyến cũng như đưa ra các tính chất giúp các bạn học sinh hiểu sâu hơn về lý thuyết. Phần bài tập được sưu tầm và chọn lọc để các bạn học sinh có thể áp dụng các tính chất phía trên để làm bài. Qua đó sẽ giúp cho các bạn học sinh ôn tập và củng cố, nâng cao thêm kiến thức về phần Tiếp tuyến nói riêng và Hình học lớp 9 nói chung để chuẩn bị cho kì thi tuyển sinh vào lớp 10.
Lưu ý: Nếu không tìm thấy nút Tải về bài viết này, bạn vui lòng kéo xuống cuối bài viết để tải về.
Học trực tuyến lớp 9 môn Toán chuyên đề: Tiếp tuyến với đường tròn
Các bài toán về tiếp tuyến và cát tuyến
1. Những tính chất cần nhớ về tiếp tuyến và cát tuyến
+ Nếu hai đường thẳng chứa các dây AB, CD, KCD của một đường tròn cắt nhau tại M thì MA.MB = MC . MD
+ Đảo lại nếu hai đường thẳng AB, CD cắt nhau tại M và MA.MB = MC.MD thì bốn điểm a, B, C, D thuộc một đường tròn.
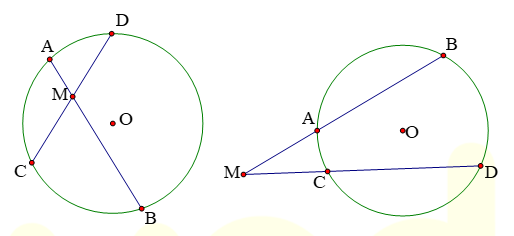
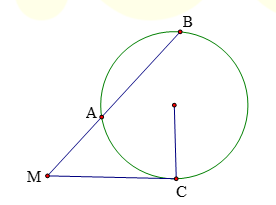
+ Nếu MC là tiếp tuyến và MAB là cát tuyến thì MC² = MA.MB = MO² - R²
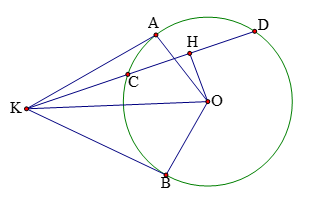
+ Từ điểm K nằm ngoài đường tròn ta kẻ các tiếp tuyến KA, KB cát tuyến KCD, H là trung điểm CD thì năm điểm K, A, H, O, B nằm trên một đường tròn.
+ Từ điểm K nằm ngoài đường tròn ta kẻ các tiếp tuyến KA, KB cát tuyến KCD thì ![]() .
.
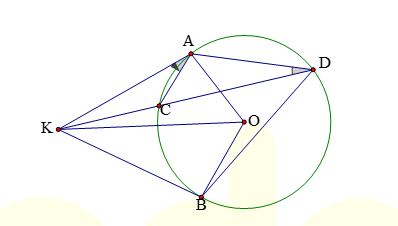
2. Một số bài toán về tiếp tuyến và cát tuyến
Bài 1: Từ điểm A nằm ngoài đường tròn O, kẻ tiếp tuyến AB, AC và cát tuyến ADE. Dây cung EN song song với BC. I là giao điểm của DN và BC. Chứng minh rằng IB = IC.
Hướng dẫn giải
Hình vẽ minh họa
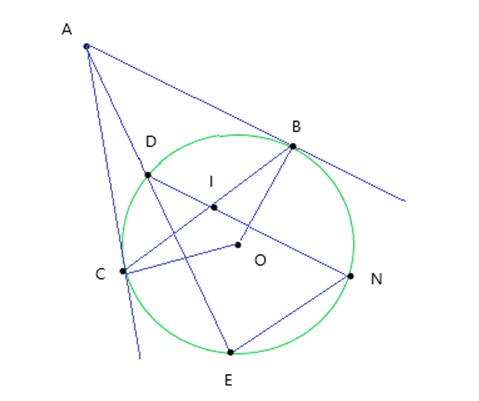
Xét tứ giác ABOC có:
![]() (tính chất tiếp tuyến)
(tính chất tiếp tuyến)
![]()
Mà 2 góc này ở vị trí đối nhau nên tứ giác ABOC nội tiếp đường tròn
Xét tam giác CIK và tam giác BIC ta có
![]() chung
chung
![]() (góc tạo bởi tia tiếp tuyến và dây cung bằng góc nội tiếp chắn cùng cung đó)
(góc tạo bởi tia tiếp tuyến và dây cung bằng góc nội tiếp chắn cùng cung đó)
Suy ra tam giác CIK đồng dạng với tam giác BIC
![]()
Vì AC // BD nên ![]() (góc trong cùng phía)
(góc trong cùng phía)
![]()
Mà tam giác BOD cân ở O (OB = OD = R)
![]()
Áp dụng tính chất tiếp tuyến cắt nhau suy ra ![]()
![]()
Nhận thấy ![]()
Mà 2 góc ở vị trí kề nhau suy ra A, O, D thẳng hàng
Bài 2: Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a, Chứng minh rằng ta luôn có MI² = MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b, Khi cho MT = 20cm, MB = 50cm, tính bán kính đường tròn?
Hướng dẫn giải
Hình vẽ minh họa
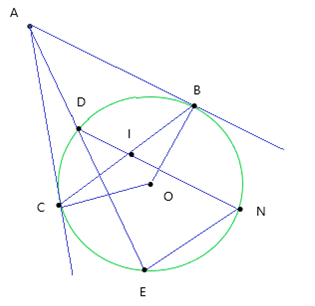
a, Xét hai tam giác BMT và TMA có
![]() chung
chung
![]() (cùng chắn cung nhỏ AT)
(cùng chắn cung nhỏ AT)
Suy ra tam giác BMT đồng dạng với tam giác TMA
![]()
Vì cát tuyến MAB kẻ tùy ý nên ta luôn có ![]() không phụ thuộc vị trí của cát tuyến MAB
không phụ thuộc vị trí của cát tuyến MAB
b, Gọi bán kính đường tròn là R. Ta có
![]()
![]()
Thay số ta có
![]()
![]()
![]()
Bài 3:Từ điểm K nằm ngoài đường tròn ta kẻ các tiếp tuyến KA, KB cát tuyến KCD đến (O). Gọi M là giao điểm OK và AB. Vẽ dây DI qua M. Chứng minh:
a) KIOD là tứ giác nội tiếp
b) KO là phân giác của góc IKD.
Hướng dẫn giải
Hình vẽ minh họa
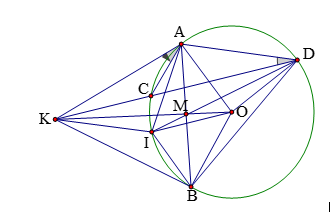
a. Để chứng minh ![]() là tứ giác nội tiếp việc chỉ ra các góc là rất khó khăn.
là tứ giác nội tiếp việc chỉ ra các góc là rất khó khăn.
Ta phải dựa vào các tính chất của cát tuyến, tiếp tuyến.
Ta có: ![]() là tứ giác nội tiếp và
là tứ giác nội tiếp và ![]() nên ta có:
nên ta có: ![]()
Mặt khác ![]() là tứ giác nội tiếp nên
là tứ giác nội tiếp nên ![]()
Từ đó suy ra ![]() hay
hay ![]() là tứ giác nội tiếp.
là tứ giác nội tiếp.
b. Đường tròn ngoại tiếp tứ giác ![]() có
có ![]()
suy ra ![]() là phân giác của góc
là phân giác của góc ![]()
Bài 4: Từ điểm K nằm ngoài đường tròn (O) ta kẻ các tiếp tuyến KA, KB cát tuyến KCD đến (O). Gọi M là giao điểm OK và AB. Chứng minh
a) CMOD là tứ giác nội tiếp
b) Đường thẳng AB chứa phân giác của góc CMD.
Hướng dẫn giải
Hình vẽ minh họa
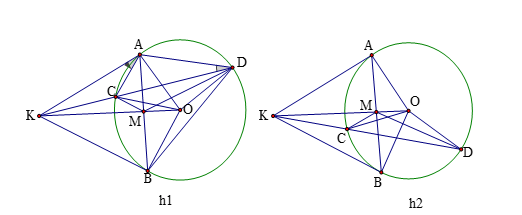
a. Vì ![]() là tiếp tuyến nên ta có:
là tiếp tuyến nên ta có: ![]()
Mặt khác tam giác ![]() vuông tại
vuông tại ![]() và
và ![]() nên
nên ![]() suy ra
suy ra ![]() hay
hay ![]() là tứ giác nội tiếp .
là tứ giác nội tiếp .
![]() là tứ giác nội tiếp nên
là tứ giác nội tiếp nên ![]() .
.
Mặt khác ta có: ![]()
Trường hợp 1:
Tia ![]() thuộc nửa mặt phẳng chứa
thuộc nửa mặt phẳng chứa ![]() và bờ là
và bờ là ![]() (h1)
(h1)
Hai góc ![]() có 2 góc phụ với nó tương ứng là
có 2 góc phụ với nó tương ứng là ![]() mà
mà ![]() nên
nên ![]() hay
hay ![]() là tia phân giác của góc
là tia phân giác của góc ![]()
Trường hợp 2:
Tia ![]() thuộc nửa mặt phẳng chứa
thuộc nửa mặt phẳng chứa ![]() và bờ là
và bờ là ![]() (h2) thì tương tự ta cũng có
(h2) thì tương tự ta cũng có ![]() là tia phân giác của góc
là tia phân giác của góc ![]()
Suy ra: Đường thẳng ![]() chứa phân giác của góc
chứa phân giác của góc ![]() .
.
Bài 5: Từ điểm K nằm ngoài đường tròn (O) ta kẻ các tiếp tuyến KA, KB cát tuyến KCD đến (O). Gọi là trung điểm CD. Vẽ dây AF đi qua H. Chứng minh BF // CD
Hướng dẫn giải
Hình vẽ minh họa
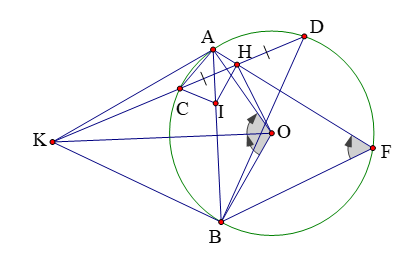
Ta có ![]() .
.
Mặt khác ![]() cùng chắn cung
cùng chắn cung ![]() nên suy ra
nên suy ra ![]() hay
hay ![]() là tứ giác nội tiếp.
là tứ giác nội tiếp.
Do đó ![]() .
.
Mặt khác ta có ![]() cùng nằm trên đường tròn đường kính
cùng nằm trên đường tròn đường kính ![]()
![]() nên
nên ![]()
Mà ![]()
Nhận xét: Mấu chốt bài toán nằm ở vấn đề ![]() .Thay vì chứng minh
.Thay vì chứng minh ![]() ta chứng minh
ta chứng minh ![]() .
.
Bài 6: Cho đường tròn ![]() dây cung
dây cung ![]() . Gọi
. Gọi ![]() là điểm đối xứng với
là điểm đối xứng với ![]() qua
qua ![]() . Kẻ tiếp tuyến
. Kẻ tiếp tuyến ![]() với đường tròn
với đường tròn ![]() . Tiếp tuyến của đường tròn
. Tiếp tuyến của đường tròn ![]() tại
tại ![]() cắt
cắt ![]() ở
ở ![]() . Gọi
. Gọi ![]() là giao điểm thứ hai của
là giao điểm thứ hai của ![]() với đường tròn
với đường tròn ![]() . Chứng minh rằng
. Chứng minh rằng ![]() .
.
Giải:
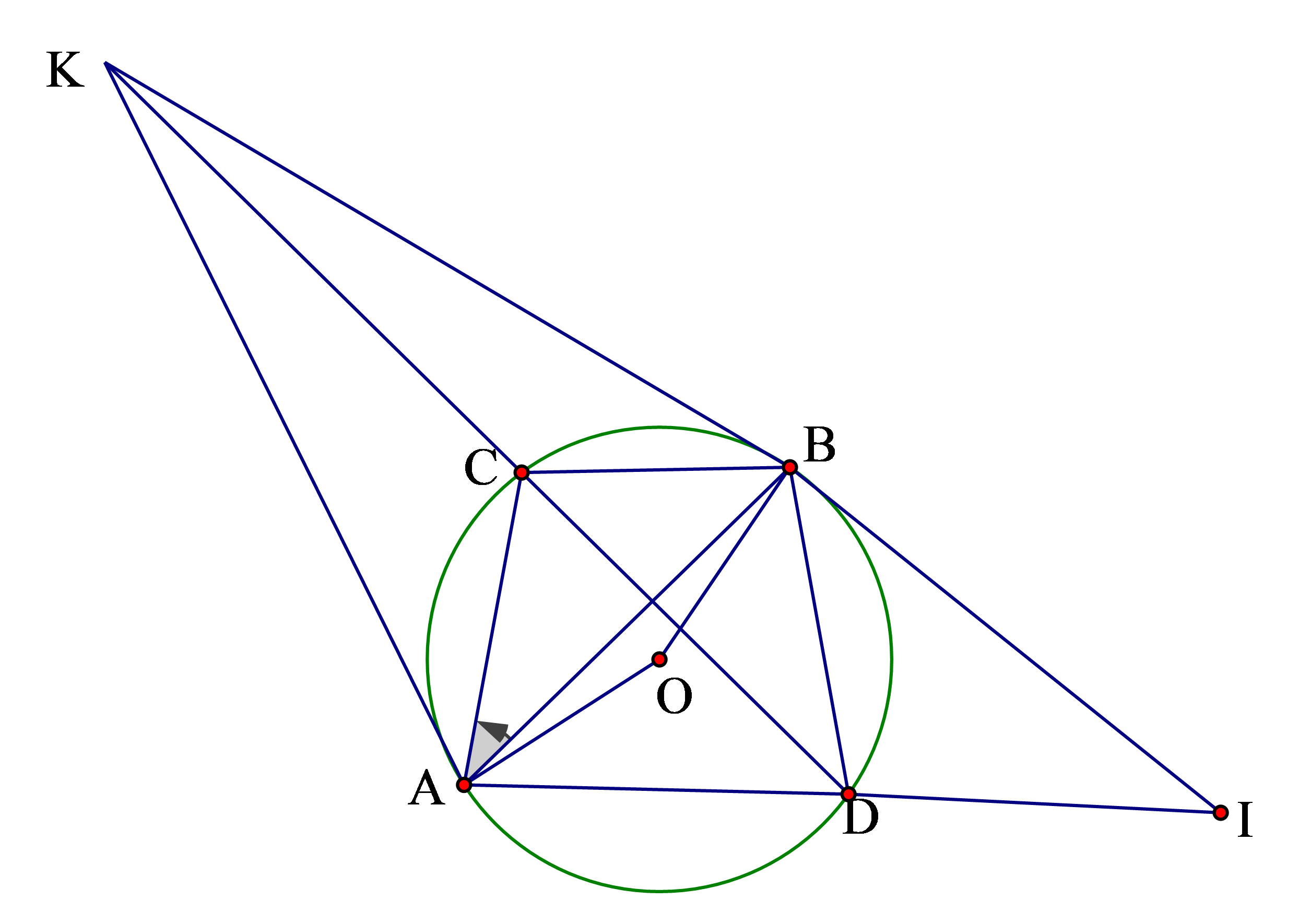
Ta cần chứng minh: ![]()
Mặt khác ta có: ![]() nên ta sẽ chứng minh
nên ta sẽ chứng minh ![]() hay
hay ![]()
Thật vậy theo tính chất 5 ta có: ![]() mà
mà ![]()
Tứ giác ![]() nội tiếp nên
nội tiếp nên ![]()
![]()
Hay ![]()
Bài 7: Từ điểm ![]() nằm ngoài đường tròn ta
nằm ngoài đường tròn ta ![]() kẻ các tiếp tuyến
kẻ các tiếp tuyến ![]() cát tuyến
cát tuyến ![]() đến
đến ![]() . Gọi
. Gọi ![]() là giao điểm
là giao điểm ![]() và
và ![]() . Vẽ dây
. Vẽ dây ![]() qua
qua ![]() . Chứng minh
. Chứng minh ![]()
Giải:
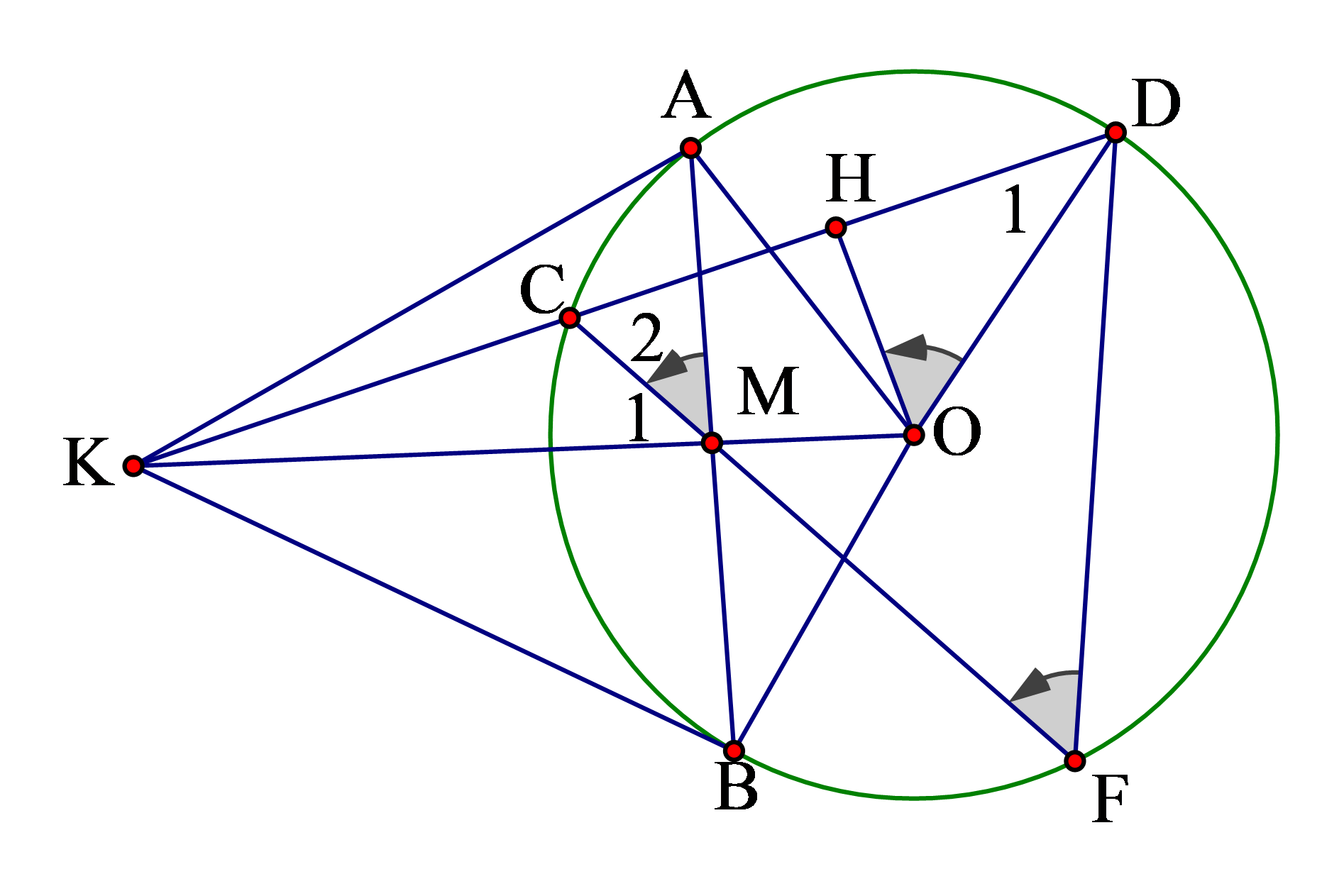
Kẻ ![]()
Ta chứng minh được: ![]() là tứ giác nội tiếp (bài toán 2) nên
là tứ giác nội tiếp (bài toán 2) nên ![]() mà
mà ![]() .
.
Mặt khác ta có: ![]() .
.
Từ đó suy ra ![]()
Chú ý: ![]() là hình thang cân có hai đáy là
là hình thang cân có hai đáy là ![]()
Bài 8: Từ điểm ![]() nằm ngoài đường tròn ta
nằm ngoài đường tròn ta ![]() kẻ các tiếp tuyến
kẻ các tiếp tuyến ![]() cát tuyến
cát tuyến ![]() đến
đến ![]() . Gọi
. Gọi ![]() là giao điểm
là giao điểm ![]() và
và ![]() . Kẻ
. Kẻ ![]() vuông góc với
vuông góc với ![]() cắt
cắt ![]() ở
ở ![]() . Chứng minh
. Chứng minh
a. ![]() là tứ giác nội tiếp
là tứ giác nội tiếp
b. ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn ![]()
Giải:
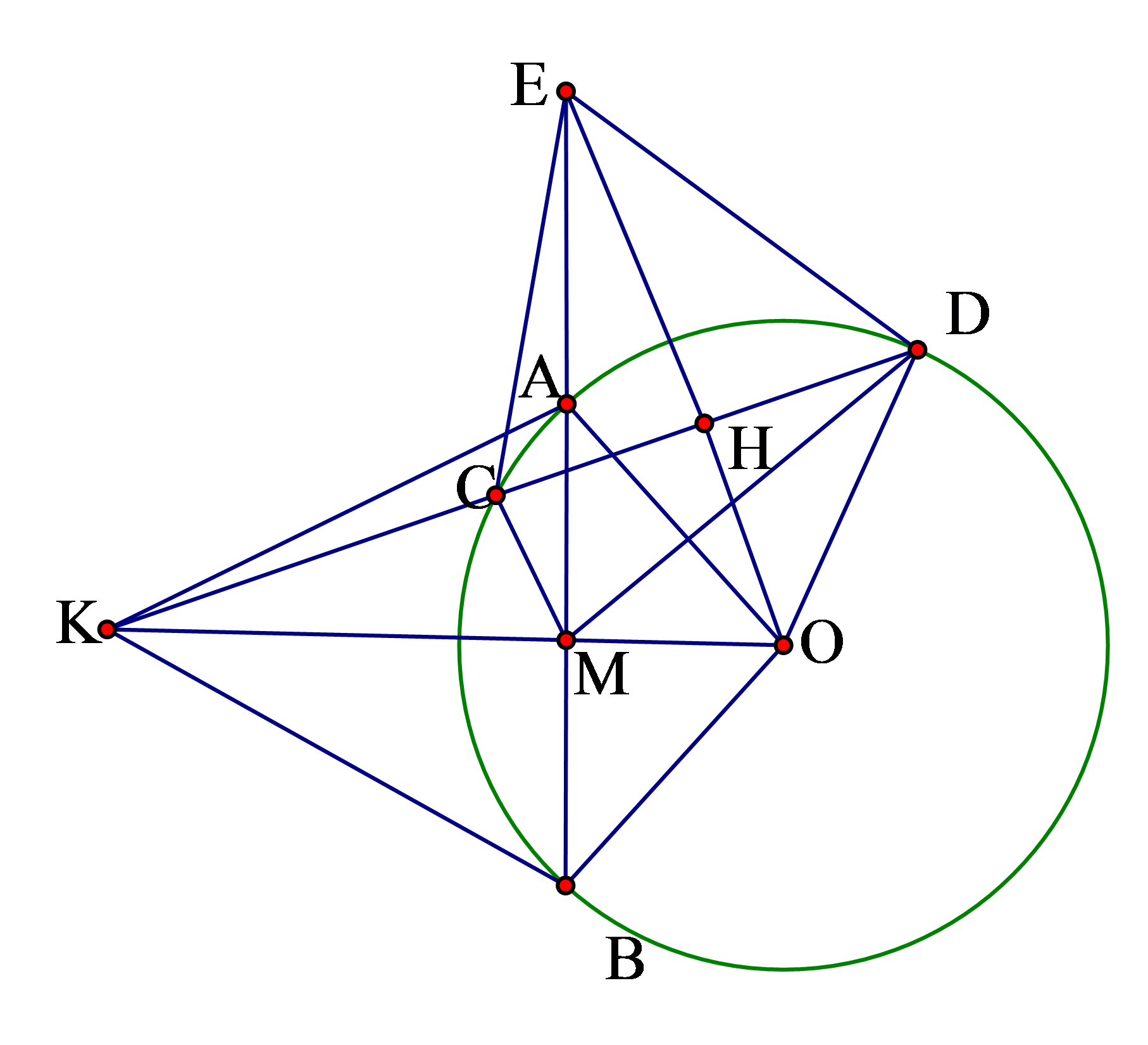
a. Theo bài toán 2, ta có ![]() là tứ giác nội tiếp nên
là tứ giác nội tiếp nên ![]() .
.
Do đó các góc phụ với chúng bằng nhau: ![]() .
.
Suy ra ![]() là tứ giác nội tiếp (theo cung chứa góc).
là tứ giác nội tiếp (theo cung chứa góc).
b. Cũng theo bài toán 2, ![]() nội tiếp.
nội tiếp.
Mặt khác ![]() là tứ giác nội tiếp nên
là tứ giác nội tiếp nên ![]() thuộc một đường tròn.
thuộc một đường tròn.
Từ đó dễ chứng minh ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn ![]()
Bài 9: Từ điểm ![]() nằm ngoài đường tròn ta
nằm ngoài đường tròn ta ![]() kẻ các tiếp tuyến
kẻ các tiếp tuyến ![]() cát tuyến
cát tuyến ![]() đến
đến ![]() . Vẽ đường kính
. Vẽ đường kính ![]() . Các dây
. Các dây ![]() cắt
cắt ![]() theo thứ tự ở
theo thứ tự ở ![]() . Chứng minh rằng
. Chứng minh rằng ![]() .
.
Giải:
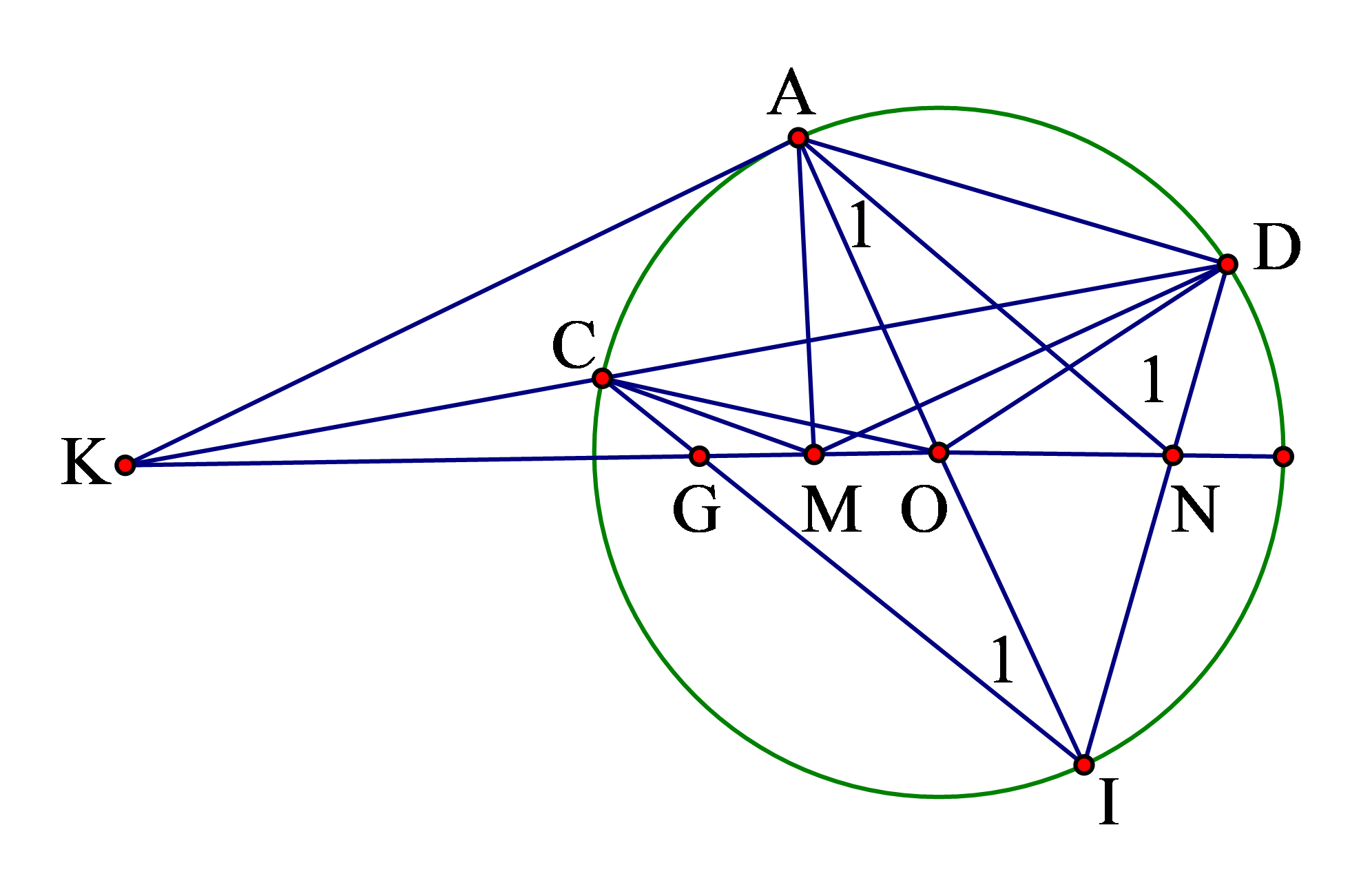
Ta vẽ trong hình trường hợp ![]() và
và ![]() nằm khác phía đối với
nằm khác phía đối với ![]() . Các trường hợp khác chứng minh tương tự.
. Các trường hợp khác chứng minh tương tự.
Để chứng minh ![]() , ta sẽ chứng minh
, ta sẽ chứng minh ![]() .
.
Ta đã có ![]() , cần chứng minh
, cần chứng minh ![]() , muốn vậy phải có
, muốn vậy phải có ![]() . Ta sẽ chứng minh
. Ta sẽ chứng minh ![]() .
.
Chú ý đến ![]() là đường kính, ta có
là đường kính, ta có ![]() , do đó ta kẻ
, do đó ta kẻ ![]() Ta có
Ta có ![]() là tứ giác nội tiếp, suy ra
là tứ giác nội tiếp, suy ra ![]() (1)
(1)
Sử dụng bài 2, ta có ![]() là tứ giác nội tiếp và
là tứ giác nội tiếp và ![]() (2). Từ (1) và (2) suy ra
(2). Từ (1) và (2) suy ra ![]() .
.
Ta lại có ![]() nên
nên ![]() .
.
HS tự giải tiếp.
Bài 10: Từ điểm ![]() nằm ngoài đường tròn ta
nằm ngoài đường tròn ta ![]() kẻ các tiếp tuyến
kẻ các tiếp tuyến ![]() cát tuyến
cát tuyến ![]() đến
đến ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Chứng minh rằng
. Chứng minh rằng ![]() .
.
Giải:
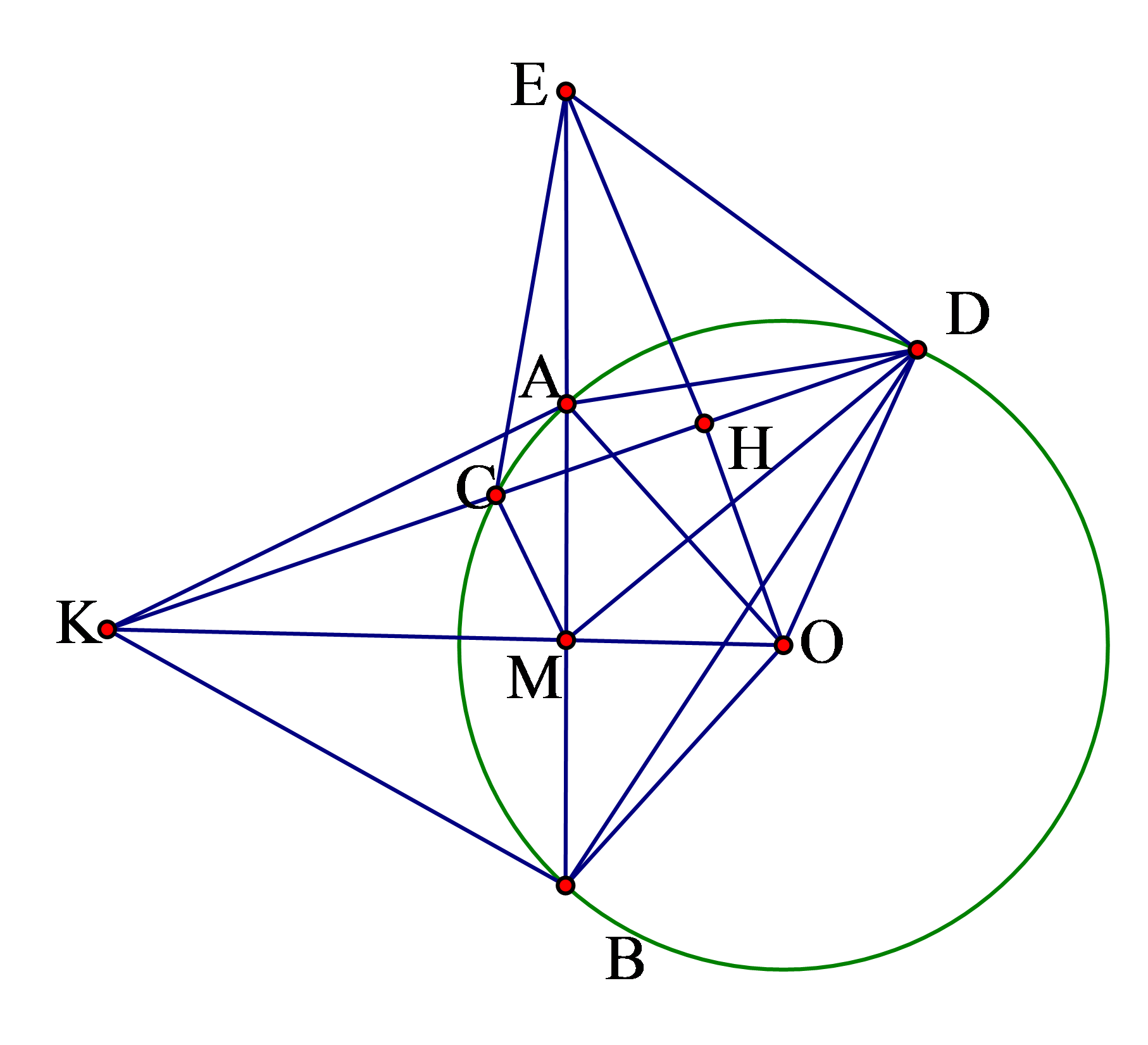
Kẻ ![]() , cắt
, cắt ![]() ở
ở ![]() .
.
Theo bài 7, ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn ![]() , nên theo bài toán quen thuộc 3, ta có
, nên theo bài toán quen thuộc 3, ta có ![]() là tứ giác nội tiếp, suy ra
là tứ giác nội tiếp, suy ra ![]() (2).
(2).
Từ (1) và (2) suy ra ![]() .
.
Do đó hai góc bù với nhau chúng bằng nhau: ![]() (g.g) nên
(g.g) nên ![]() .
.
Bài 11: Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì ( M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB. Chứng minh tứ giác AMBO nội tiếp.
- Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn .
- Chứng minh OI.OM = R2; OI. IM = IA2.
- Chứng minh OAHB là hình thoi.
- Chứng minh ba điểm O, H, M thẳng hàng.
- Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d
Lời giải:
Hình vẽ minh họa:
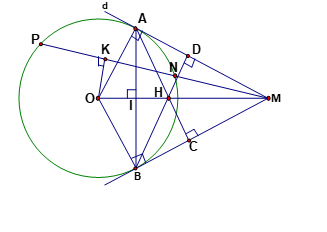
1. (HS tự làm).
2. Vì K là trung điểm NP nên OK ⊥ NP (quan hệ đường kính và dây cung) => ∠OKM = 900. Theo tính chất tiếp tuyến ta có ∠OAM = 900; ∠OBM = 900. như vậy K, A, B cùng nhìn OM dưới một góc 900 nên cùng nằm trên đường tròn đường kính OM.
Vậy năm điểm O, K, A, M, B cùng nằm trên một đường tròn.
3. Ta có MA = MB (tính chất hai tiếp tuyến cắt nhau); OA = OB = R
=> OM là trung trực của AB => OM ⊥ AB tại I .
Theo tính chất tiếp tuyến ta có ∠OAM = 900 nên tam giác OAM vuông tại A có AI là đường cao.
Áp dụng hệ thức giữa cạnh và đường cao => OI.OM = OA2 hay OI.OM = R2; và OI. IM = IA2.
4. Ta có OB ⊥ MB (tính chất tiếp tuyến) ; AC ⊥ MB (gt) => OB // AC hay OB // AH.
OA ⊥ MA (tính chất tiếp tuyến) ; BD ⊥ MA (gt) => OA // BD hay OA // BH.
=> Tứ giác OAHB là hình bình hành; lại có OA = OB (= R) => OAHB là hình thoi.
5. Theo trên OAHB là hình thoi. => OH ⊥ AB; cũng theo trên OM ⊥ AB => O, H, M thẳng hàng (Vì qua O chỉ có một đường thẳng vuông góc với AB).
6. (HD) Theo trên OAHB là hình thoi. => AH = AO = R. Vậy khi M di động trên d thì H cũng di động nhưng luôn cách A cố định một khoảng bằng R. Do đó quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A bán kính AH = R.
🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.
------------------------------------------------------
Dạng toán tiếp tuyến và cát tuyến không chỉ giúp học sinh củng cố kiến thức hình học cơ bản mà còn rèn luyện khả năng tư duy logic và kỹ năng trình bày bài toán hình học chặt chẽ – điều rất cần thiết trong kỳ thi vào lớp 10. Qua việc luyện tập với các bài toán có đáp án, học sinh sẽ làm quen với nhiều tình huống khác nhau: từ chứng minh hình học, tính toán độ dài, đến áp dụng định lý liên quan đến góc, cung và tiếp tuyến. Để đạt kết quả cao, các em nên kết hợp ôn tập dạng bài này với các chuyên đề quan trọng khác như tứ giác nội tiếp, tam giác đồng dạng, đường tròn ngoại tiếp. Đừng quên lưu lại bài viết này và chia sẻ với bạn bè cùng ôn thi nhé!










