Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán

Bài tập nâng cao lớp 9 môn Toán

Bài trước

Bài sau

Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán được VnDoc tổng hợp và chia sẻ tới các bạn học sinh nhằm giúp các bạn có thêm nhiều bài tập tham khảo, chuẩn bị tốt cho kỳ thi HSG lớp 9 sắp tới, các thầy cô giáo cũng có thể tham khảo để ra đề thi cho các bạn học sinh.

Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông
Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn
Bồi dưỡng HSG Toán 9 chuyên đề 3: Góc với đường tròn
Bồi dưỡng HSG Toán 9 chuyên đề 4: Một số tiêu chuẩn nhận biết tứ giác nội tiếp
Bồi dưỡng HSG Toán 9 chuyên đề 5: Chùm bài Toán về Tiếp tuyến, Cát tuyến
Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng
Bồi dưỡng HSG Toán 9 chuyên đề 7: Một số bài tập chọn lọc hình học phẳng
Bồi dưỡng HSG Toán 9 chuyên đề 8: Một số bài bài tập chọn lọc các đề thi học sinh giỏi
Bồi dưỡng HSG Toán 9 chuyên đề 9: Quỹ tích
Bồi dưỡng HSG Toán 9 chuyên đề 10: Bất đẳng thức Hình học
Bồi dưỡng HSG Toán 9: Hướng dẫn giải bài tập nâng cao theo chuyên đề

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

Lý thuyết các hệ thức lượng trong tam giác và giải tam giác

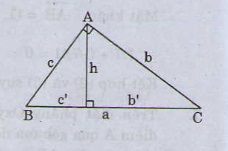
Nhắc lại hệ thức lượng trong tam giác vuông.

Cho tam giác vuông góc tại đỉnh $A (\widehat{A} = 90^0)$ $A (\widehat{A} = 90^0)$, ta có:

$1. {b^2} = ab$ $1. {b^2} = ab';{c^2} = a.c'$

2. Định lý Pitago: ${a^2} = {b^2} + {c^2}$ ${a^2} = {b^2} + {c^2}$

$3. a.h = b.c$

$4. h^2= b’.c’$

$5. \frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ $5. \frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$

Bồi dưỡng HSG Toán 9: Bài tập nâng cao chuyên đề 1

1. Định lý cosin

Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với $cosin$ của góc xen giữa chúng.

Ta có các hệ thức sau:

${a^2} = {b^2} + {c^2} - 2bc.{\mathop{\rm cosA}\nolimits} (1)$ ${a^2} = {b^2} + {c^2} - 2bc.{\mathop{\rm cosA}\nolimits} (1)$
${b^2} = {a^2} + {c^2} - 2ac{\mathop{\rm cosB}\nolimits} (1)$ ${b^2} = {a^2} + {c^2} - 2ac{\mathop{\rm cosB}\nolimits} (1)$
${c^2} = {a^2} + {b^2} - 2bc\cos C(3)$ ${c^2} = {a^2} + {b^2} - 2bc\cos C(3)$

$\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc} \cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac}$ $\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc} \cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac}$

$\cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab}$ $\cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab}$

Áp dụng: Tính độ dài đường trung tuyến của tam giác:

Cho tam giác có các cạnh $BC = a, CA = b$ và $AB = c$. Gọi $m_a,m_b$ và $m_c$ là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh $A, B, C$ của tam giác. Ta có

${m_{a}}^{2} = \frac{2.(b^{2}+c^{2})-a^{2}}{4}$ ${m_{a}}^{2} = \frac{2.(b^{2}+c^{2})-a^{2}}{4}$

${m_{b}}^{2} = \frac{2.(a^{2}+c^{2})-b^{2}}{4}$ ${m_{b}}^{2} = \frac{2.(a^{2}+c^{2})-b^{2}}{4}$

${m_{c}}^{2} = \frac{2.(a^{2}+b^{2})-c^{2}}{4}$ ${m_{c}}^{2} = \frac{2.(a^{2}+b^{2})-c^{2}}{4}$

Bồi dưỡng HSG Toán 9: Bài tập nâng cao chuyên đề 1

2. Định lí sin

Định lí: Trong tam giác bất kỳ, tỉ số giữa một cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là

$\frac{a}{sin A}= \frac{b}{sin B} = \frac{c}{sin C} = 2R$ $\frac{a}{sin A}= \frac{b}{sin B} = \frac{c}{sin C} = 2R$

với $R$ là bán kính đường tròn ngoại tiếp tam giác

Công thức tính diện tích tam giác:

Ta kí hiệu h_a, h_b và h_clà các đường cao của tam giác lần lượt vẽ từ các đình $A, B, C$ và $S$ là diện tích tam giác đó.

Diện tích $S$ của tam giác được tính theo một trong các công thức sau

$S = \frac{1}{2} ab \sin C= \frac{1}{2} bc \sin A = \frac{1}{2}ca \sin B\ (1)$ $S = \frac{1}{2} ab \sin C= \frac{1}{2} bc \sin A = \frac{1}{2}ca \sin B\ (1)$

$S = \frac{abc}{4R}\ (2)$ $S = \frac{abc}{4R}\ (2)$

$S = pr\ (3)$ $S = pr\ (3)$ $S = \sqrt{p(p - a)(p - b)(p - c)}\ (công\ thức\ Hê - rông)\ (4)$ $S = \sqrt{p(p - a)(p - b)(p - c)}\ (công\ thức\ Hê - rông)\ (4)$

3. Giải tam giác và ứng dụng vào việc đo đạc

Giải tam giác: Giải tam giác là tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.

Muốn giải tam giác ta cần tìm mối liên hệ giữa các yếu tố đã cho với các yếu tố chưa biết của tam giác thông qua các hệ thức đã được nêu trong định lí cosin, định lí sin và các công thức tính diện tích tam giác.

Các bài toán về giải tam giác: Có 3 bài toán cơ bản về giải tam giác:

a) Giải tam giác khi biết một cạnh và hai góc.

Đối với bài toán này ta sử dụng định lí sin để tính cạnh còn lại

b) Giải tam giác khi biết hai cạnh và góc xen giữa

Đối với bài toán này ta sử dụng định lí cosin để tính cạnh thứ ba

c) Giải tam giác khi biết ba cạnh

Đối với bài toán này ta sử dụng định lí cosin để tính góc

$\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc}$ $\cos A = \frac{b^{2}+c^{2}-a^{2}}{2bc}$

$\cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac}$ $\cos B = \frac{a^{2}+c^{2}-b^{2}}{2ac}$

$cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab}$ $cos C = \frac{a^{2}+b^{2}-c^{2}}{2ab}$

Tham khảo thêm: Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

Ngoài ra các bạn làm thêm bài tập nâng cao: Bồi dưỡng HSG Toán 9: Bài tập nâng cao chuyên đề 1.

Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

Lý thuyết đường tròn

1. Đường tròn

Đường tròn tâm O bán kính R là hình gồm các điểm cách O một khoảng bằng R.

2. Vị trí tương đối của một điểm với đường tròn

Cho đường tròn (O;R) và điểm M

Điểm M nằm trên đường tròn (O; R) ⇔ OM = R
Điểm M nằm trong đường tròn (O; R) ⇔ OM < R
Điểm M nằm ngoài đường tròn (O; R) ⇔ OM > R

3. Cách xác định đường tròn

C1: Biết tâm và bán kính
C2: Biết đường kính
C3: Qua điểm thẳng hàng

4. Tính chất đối xứng

Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó
Đường tròn có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn (đường tròn có vô số trục đối xứng)

Tham khảo thêm: Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

Bài tập nâng cao: Bồi dưỡng HSG Toán 9: Bài tập nâng cao chuyên đề 2

Bồi dưỡng HSG Toán 9 chuyên đề 3: Góc với đường tròn

1. Định nghĩa

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Cung nằm bên trong góc là cung bị chắn.

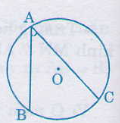
Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán

2. Định lí

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

3. Hệ quả

Trong một đường tròn:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng 90⁰) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông

Tham khảo thêm: Bồi dưỡng HSG Toán 9 chuyên đề 3: Góc với đường tròn

Bồi dưỡng HSG Toán 9 chuyên đề 4: Một số tiêu chuẩn nhận biết tứ giác nội tiếp

1. Định nghĩa

Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)

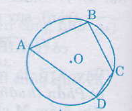
Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán

2. Định lí

Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng $180^0$

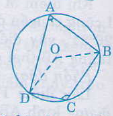
Ví dụ: Tứ giác $ABCD$ nội tiếp đường tròn $(O)$

$=> \left\{\begin{matrix} \widehat{A}+\widehat{C}=180^{\circ}\\ \widehat{B}+\widehat{D}=180^{\circ} \end{matrix}\right.$ $=> \left\{\begin{matrix} \widehat{A}+\widehat{C}=180^{\circ}\\ \widehat{B}+\widehat{D}=180^{\circ} \end{matrix}\right.$

Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán

3. Định lí đảo

Nếu tứ giác có tổng số đo hai góc đối diện bằng $180^0$ thì tứ giác đó nội tiếp được đường tròn.

4. Một số dấu hiệu nhận biết tứ giác nội tiếp

- Tứ giác có tổng hai góc đối bằng $180^\circ$ $180^\circ$.

- Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.

- Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.

- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc $\alpha.$ $\alpha.$

Tham khảo thêm: Bồi dưỡng HSG Toán 9 chuyên đề 4: Một số tiêu chuẩn nhận biết tứ giác nội tiếp

Bồi dưỡng HSG Toán 9 chuyên đề 5: Chùm bài Toán về Tiếp tuyến, Cát tuyến

Tiếp tuyến là gì?

Tiếp tuyến (tangent) là đường thẳng chỉ tiếp xúc, chứ không cắt đồ thị tại một điểm nhất định. Khái niệm tiếp tuyến có ích khi được vận dụng vào kinh tế để xác định độ dốc hay hệ số góc của một đường tại một điểm nhất định dọc theo hướng đó. Ví dụ, phân tích đường bàng quan cho thấy người tiêu dùng hành động hợp lý sẽ tìm cách tối đa hóa ích lợi của mình bằn cách chọn một kết hợp hai sản phẩm X và Y sao cho đường ngân sách của anh ta tiếp tuyến với đường bàng quan cao nhất có thể có, bởi vì chỉ tại điểm đó giá tương đối của các sản phẩm mới phù hợp với lợi ích tương đối của chúng.

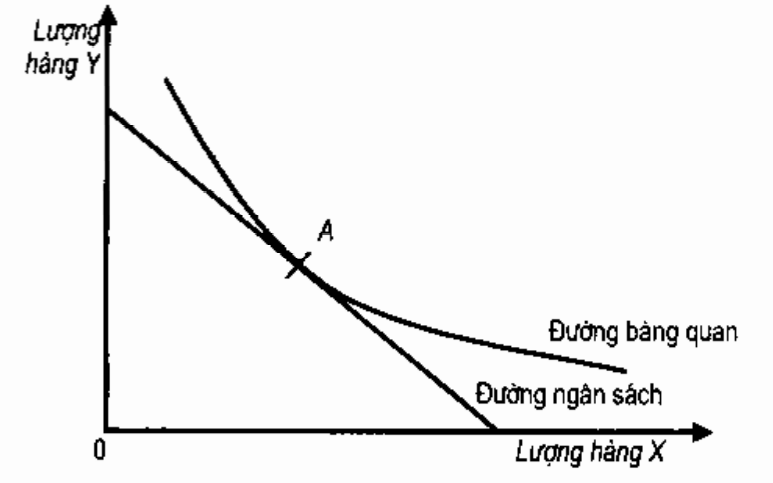
Chuyên đề 5: Chùm bài Toán về Tiếp tuyến, Cát tuyến

Khi tiếp tuyến đi qua điểm giao của đường tiếp tuyến và đường cong trên, được gọi là tiếp điểm, đường tiếp tuyến "đi theo hướng" của đường cong, và do đó là đường thẳng xấp xỉ tốt nhất với đường cong tại điểm tiếp xúc đó.

Tương tự như vậy, mặt phẳng tiếp tuyến của mặt cong tại một điểm nhất định là mặt phẳng "chỉ chạm vào" mặt cong tại điểm đó. Khái niệm tiếp tuyến là một trong những khái niệm cơ bản nhất trong hình học vi phân và đã được nghiên cứu và tổng quát hóa rộng rãi.

Định nghĩa về cát tuyến

Cát tuyến là gì? Cát tuyến là một từ Hán - Việt. Trong đó “Cát” nghĩa là cắt, còn “tuyến” có nghĩa là đường thẳng. Bởi vậy, cát tuyến chính là một đường thẳng cắt các đường khác (đường thẳng, đường tròn, đường cong,…)

Theo khái niệm trong sách giáo khoa bộ môn toán, thì cát tuyến chính là một đường thẳng cắt một đường thẳng khác. Cát tuyến của đường tròn chính là 1 đường thẳng cắt đường tròn đó tại hai điểm phân biệt. Cát tuyến của 2 đường thẳng là 1 đường thẳng cắt 2 đường thẳng trên. Một vài trường hợp đặc biệt đó chính là cát tuyến đi qua tâm đường tròn.

Để biết thêm lý thuyết: Cát tuyến là gì? Cát tuyến của đường tròn là gì?

Tham khảo thêm bài tập Chùm bài Toán về Tiếp tuyến, Cát tuyến

Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng

Định lí Ta-lét trong tam giác

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Định lí Ta-lét đảo

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Các bạn tham khảo thêm: Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng

Bồi dưỡng HSG Toán 9 chuyên đề 7: Một số bài tập chọn lọc hình học phẳng

Chuyên đề 7: Một số bài tập chọn lọc hình học phẳng

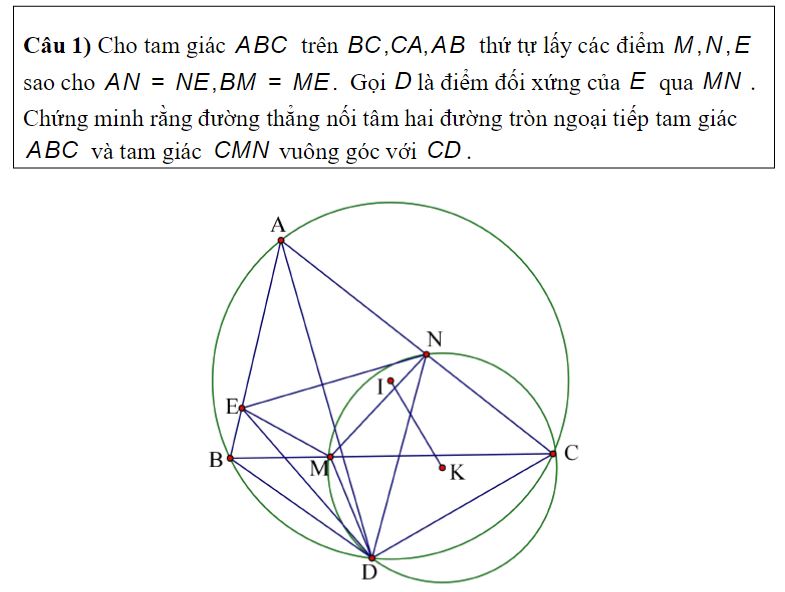
Tham khảo thêm: Chuyên đề 7: Một số bài tập chọn lọc hình học phẳng

Bồi dưỡng HSG Toán 9 chuyên đề 8: Một số bài bài tập chọn lọc các đề thi học sinh giỏi

Câu 1. (Đề thi học sinh giỏi thành phố Hà Nội – 2010)

Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $\left(O;R\right)$ $\left(O;R\right)$. $D$ là một điểm bất kỳ thuộc cung nhỏ $AD$ ($D$ khác $A$ và $C$). Gọi $M,N$ lần lượt là chân đường vuông góc kẻ từ $D$ tới các đường thẳng $AB,AC$. Gọi $P$ là giao điểm các đường thẳng $MN,BC$.

Chứng minh $DP$ và $BC$ vuông góc với nhau.

Đường tròn $\left(I;r\right)$ $\left(I;r\right)$ nội tiếp tam giác $ABC$. Tính với $IO$.

Tham khảo thêm: Bồi dưỡng HSG Toán 9 chuyên đề 8: Một số bài bài tập chọn lọc các đề thi học sinh giỏi

Bồi dưỡng HSG Toán 9 chuyên đề 9: Quỹ tích

Định nghĩa quỹ tích là gì?

Một hình H, theo định nghĩa, được gọi là quỹ tích của điểm M sẽ có tính chất T khi và chỉ khi hình H chứa các điểm có tính chất T.

Các loại quỹ tích cơ bản

Tập hợp các điểm bao gồm hai điểm A, B và tất cả những điểm nằm giữa A và B là đoạn thẳng AB.
Tập hợp các điểm cách đều hai điểm cố định chính là đường trung trực của đoạn thẳng nối hai điểm ấy.
Tập hợp các điểm cách đều hai cạnh của một góc chính là tia phân giác của góc đó.
Tập hợp các điểm cách đường thẳng (d) một khoảng bằng I là hai đường thẳng song song với (d) và sẽ cách đường thẳng (d) một khoảng chính bằng I.
Ta có tập hợp của các điểm cách điểm cố định O một khoảng bằng R chính là đường tròn tâm O, với bán kính R trong mặt phẳng và là mặt cầu tâm O, bán kính R trong không gian ba chiều.
Tập hợp các điểm M tạo với hai đầu mút của đoạn thẳng AB cho trước một góc $\widehat{AMB}$ $\widehat{AMB}$ sẽ có số đo bằng α không đổi là hai cung tròn đối xứng nhau qua AB (được gọi là cung tròn chứa góc α vẽ trên đoạn AB).
Tập hợp những cặp điểm đối xứng nhau qua một đường thẳng là mặt phẳng chứa đường thẳng đó.
Tập hợp các điểm trong mặt phẳng với tổng khoảng cách tới hai điểm cố định cho trước (nằm trong mặt phẳng đó) chính là đường elíp nhận hai điểm cố định đó là tiêu điểm.
Tập hợp các điểm cách đều một điểm và một đường thẳng cố định sẽ là đường Parabol trong mặt phẳng đi qua điểm và đường cố định đó.

Các bạn tham khảo thêm tại: Bồi dưỡng HSG Toán 9 chuyên đề 9: Quỹ tích

Bồi dưỡng HSG Toán 9 chuyên đề 10: Bất đẳng thức Hình học

I). SỬ DỤNG CÁC TÍNH CHẤT HÌNH HỌC ĐƠN GIẢN.

1) Bất đẳng thức liên hệ giữa độ dài các cạnh một tam giác.

Tham khảo thêm tại: Bồi dưỡng HSG Toán 9 chuyên đề 10: Bất đẳng thức Hình học

Bồi dưỡng HSG Toán 9: Hướng dẫn giải bài tập nâng cao theo chuyên đề

Tham khảo lời giải tại: Hướng dẫn giải bài tập nâng cao theo chuyên đề

Tài liệu trên đây được VnDoc tổng hợp từ nhiều nguồn khác nhau với mục đích mang đến cho các bạn học sinh tài liệu bổ ích, giúp các bạn học sinh nắm chắc lý thuyết cùng với bài tập được chọn lọc qua các kỳ thi học sinh giỏi lớp 9 sẽ mang đến cho các bạn nhiều kiến thức bổ ích. Chúc các ôn luyện tốt