Đề chọn học sinh giỏi tỉnh Toán THCS sở GD&ĐT Quảng Nam năm 2024 - 2025
Trang 1/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH QUẢNG NAM
(Đề thi gồm có 02 trang)
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THCS
NĂM HỌC 2024 – 2025
Môn thi: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày thi: 04/4/2025
Câu 1 (3,5 điểm).
1. Cho biểu thức
1
:
1 2
x x x
P
x x x x x x x
, với
0, 1
x x
. Rút gọn biểu thức
P
và tìm tất cả các số nguyên
x
thỏa mãn
2
P
.
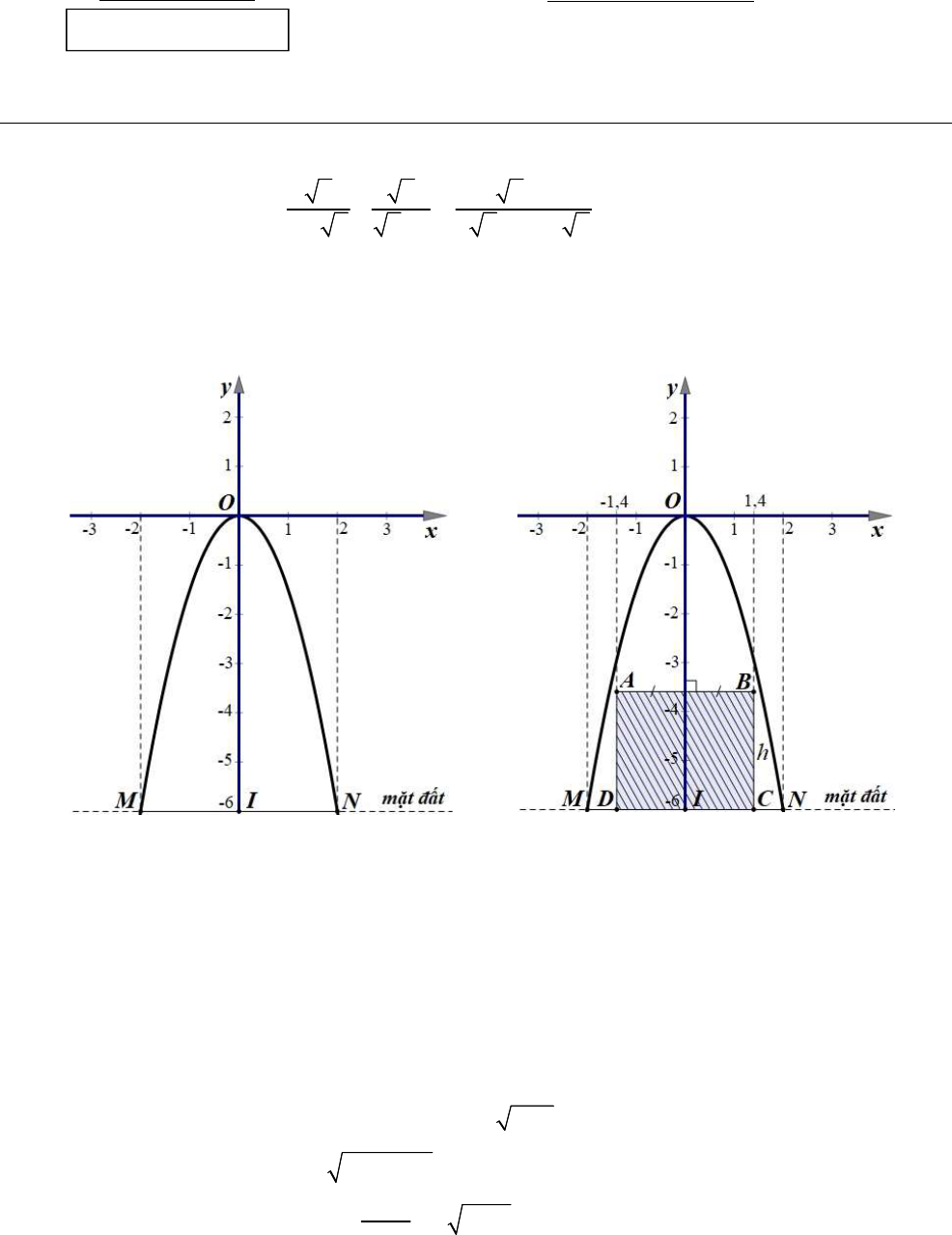
2. Một cổng nhà máy được thiết kế dạng parabol
2
0
y ax a
ở Hình 1. Chiều cao của
cổng là
6 m
IO
so với mặt đất và chiều rộng của chân cổng là
4 m.
MN
Hình 1
Hình 2
a) Tìm hệ số
a
dựa vào các dữ kiện đã cho.
b) Một cái thùng có khối lượng không lớn (kéo được trên mặt đất), dạng hình hộp chữ nhật
có chiều dài lớn hơn chiều cao của cổng, chiều rộng là AB = 2,8 m và chiều cao là BC = h (m)
(h > 0). Người ta muốn kéo thùng đó từ bên ngoài vào trong nhà máy qua vị trí chính giữa cổng
(Hình 2 minh họa thùng khi qua chính giữa cổng theo hướng nhìn từ phía trước cổng). Tìm
điều kiện của h để kéo được thùng đó qua cổng mà không chạm vào cổng.
Câu 2 (3,5 điểm).
a) Giải phương trình
2
4 15 5 2 1
x x x x
.
b) Giải hệ phương trình
2 1 15 2
2
2 2 1
1
x y y
y
x y
x
.
ĐỀ CHÍNH THỨC
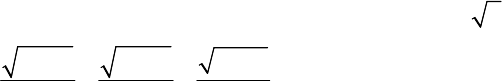
Trang 2/2
Câu 3 (1,5 điểm).
Năm học 2024-2025, trường THCS X có ba lớp 6 là
1 2 3
, ,
L L L
và ba học sinh lớp 6 là
1 2 3
, ,
H H H
đã được xếp vào ba lớp khác nhau. Ngày đầu tiên tập trung học sinh theo từng lớp,
do học sinh không biết thông tin nên cô giáo Tổng phụ trách Đội dẫn ba học sinh
1 2 3
, ,
H H H
vào ngẫu nhiên ba lớp
1 2 3
, ,
L L L
(mỗi lớp có một học sinh vào). Học sinh
H
i
vào đúng lớp của
mình nếu học sinh
H
i
vào lớp
L
i
, kí hiệu
H L
i i
(với
1;2;3
i
). Mô tả không gian mẫu và tính
xác suất để có ít nhất một học sinh vào đúng lớp của mình.
Câu 4 (3,0 điểm).
Cho tam giác ABC nhọn (AB > AC) có ba đường cao AD, BE và CF. Trên đoạn thẳng DF
lấy điểm M (M khác D và F), trên tia DE lấy điểm N sao cho
MAN BAC.
Trên cạnh AB lấy
điểm K sao cho MK song song với BC.
a) Chứng minh
AMK ANE
và hai tam giác AKE, AMN đồng dạng.
b) Chứng minh
AF.FK EF.FM
và điểm A cách đều hai đường thẳng MN, DF.
Câu 5 (4,0 điểm).
Cho tam giác ABC nhọn (AB > AC) nội tiếp đường tròn (O). Gọi M là điểm chính giữa
của cung nhỏ AB, N là điểm chính giữa của cung nhỏ AC, I là giao điểm của BN và CM.
a) Chứng minh I là tâm đường tròn nội tiếp tam giác ABC và AI vuông góc với MN.
b) Gọi X là giao điểm của OM và AB, Y là giao điểm của ON và AC. Biết MX = 4,5 và
NY = 2. Tính độ dài đoạn thẳng AI.
Câu 6 (2,5 điểm).
a) Cho hai số nguyên tố
,
p q
đều lớn hơn
5.
Tìm số dư của phép chia
30 4
p q
cho
24
.
b) Tìm hai số nguyên
,
x y
khác
0
, có ước chung lớn nhất bằng
1
và thỏa mãn
2 3 2
x x y y
.
Câu 7 (2,0 điểm).
Cho ba số thực
, ,
x y z
lớn hơn hoặc bằng
1
và thỏa mãn
2 2 2 2 2 2
3 2
x y y z z x xyz
. Tìm
giá trị lớn nhất của biểu thức
1 1
1
xy yz
zx
T
y z z x x y
.
---------- HẾT ----------
- Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
- Họ và tên thí sinh:................................................; Số báo danh......................
Trang 1/9
Câu Đáp án Điểm
Câu 1
(3,5 đ)
1. Cho biểu thức
1
:
1 2
x x x
P
x x x x x x x
, với
0, 1
x x
. Rút gọn
bi
ểu thức
P
và tìm t
ất cả các số nguy
ên
x
th
ỏa m
ãn
2
P
.
1,5
1
:
1
1 2 1
x x x
P
x
x x x x x
(Mỗi ý đặt nhân tử chung được 0,125)
0,25
2
1 1
:
1
1
x x
x
x x
(Mỗi ý được 0,125)
0,25
2
1 . 1
1 1
x x x
x x
1
x x x x
(Hai biểu thức đầu được 0,25)
0,25
2
P
trở thành
2
x x
hay
2 0
x x
, (0,125)
suy ra
1 2 0
x x
. (*) (0,125)
0,25
Vì
1 0
x
nên từ (*) suy ra
2 0
x
. Suy ra
4
x
.
(Lập luận suy ra được
2 0
x
được 0,125)
0,25
Kết hợp với
0, 1
x x
, suy ra các số nguyên
x
thỏa mãn là
2;3;4
.
0,25
2. Một cổng nhà máy được thiết kế dạng parabol
2
0
y ax a
ở Hình 1. Chiều
cao của cổng là
6 m
IO
so với mặt đất và chiều rộng của chân cổng là
4 m
MN
.
2,0
a) Tìm hệ số
a
dựa vào các dữ kiện đã cho.
0,5
Ta có
2; 6
M
,
2; 6
N
. (Chỉ cần tìm tọa độ một trong hai điểm được 0,25)
0,25
Vì parabol đi qua điểm
2; 6
N
nên
2
6 .2
a
, hay
3
2
a
. (Mỗi ý được 0,125)
0,25
b) Một cái thùng có khối lượng không lớn (kéo được trên mặt đất), dạng hình h
ộp
chữ nhật có chiều dài lớn hơn chiều cao của cổng, chiều rộng là AB = 2,8 m và chiều cao
là BC = h (m) (h > 0). Người ta muốn kéo thùng đó từ bên ngoài vào trong nhà máy
qua vị trí chính giữa cổng (Hình 2 minh họa thùng khi qua chính giữa cổng theo hư
ớng
nhìn từ phía trước cổng). Tìm điều kiện của h để kéo được thùng đó qua cổng m
à
không chạm vào cổng.
1,5
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH QUẢNG NAM
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THCS
NĂM HỌC 2024 - 2025
(Hướng dẫn chấm có 09 trang)
HƯỚNG DẪN CHẤM MÔN TOÁN
HDC CHÍNH THỨC
Đề thi HSG Toán THCS năm 2025 có đáp án
Đề chọn học sinh giỏi tỉnh Toán THCS sở GD&ĐT Quảng Nam năm 2024 - 2025 được VnDoc sưu tầm và đăng tải sau đây gồm nhiều dạng bài tập Toán khác nhau, giúp các em học sinh ôn tập, chuẩn bị cho kì thi HSG lớp 9 sắp tới. Đây cũng là tài liệu hay cho thầy cô ôn luyện đội tuyển HSG. Mời thầy cô và các em tham khảo chi tiết sau đây.
Để tham khảo thêm các tài liệu khác, mời các bạn vào chuyên mục Đề thi học sinh giỏi lớp 9 trên VnDoc với đầy đủ các môn, là tài liệu hay cho các em ôn luyện, chuẩn bị cho kì thi sắp tới đạt kết quả cao.
