Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

40 đề luyện thi học sinh giỏi Toán 9

Đề thi chọn HSG lớp 9 môn Toán

Bài trước

Bài sau

Đề thi học sinh giỏi môn Toán lớp 9

40 đề thi Học sinh giỏi Toán 9 tổng hợp 40 được VnDoc sưu tầm và tổng hợp. Bộ đề Toán dùng cho giáo viên bồi dưỡng học sinh giỏi và học sinh luyện tập trước kì thi. Với tài liệu này các bạn học sinh sẽ có thêm nhiều câu hỏi ôn tập, biết cách sắp xếp thời gian làm bài, chuẩn bị tốt cho kì thi HSG lớp 9 sắp tới. Mời các bạn tham khảo

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Đề thi học sinh giỏi môn Toán lớp 9

Thời gian: 150 phút

Câu I. ( 4 điểm). Giải phương trình

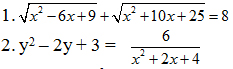
Câu II. (4 điểm)

1. Cho biểu thức:

Tìm giá trị nhỏ nhất của biểu thức A.

2. Cho a>0; b>0; c>0. Chứng minh bất đẳng thức

Câu III. (4,5 điểm)

1. Giải bài toán bằng cách lập phương trình.

Tìm số tự nhiên có hai chữ số biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 và số đó lớn hơn tổng các bình phương các chữ số của nó là 1.

2. Cho phương trình: x² –(m+1)x+2m-3 =0 (1)

+ Chứng minh rằng phương trình trên luôn có 2 nghiệm phân biệt với mọi giá trị của m.

+ Tìm giá trị của m để phương trình (1) có nghiệm bằng 3.

Câu IV (4 điểm)

Cho hình thang cân ABCD, (AB//CD; AB > CD). Hai đường chéo AC và BD cắt nhau tại I. Góc ACD = 600; gọi E; F; M lần lượt là trung điểm của các đoạn thẳng IA; ID; BC.

- Chứng minh tứ giác BEFC nội tiếp được trong một đường tròn.

- Chứng minh tam giác MEF là tam giác đều.

Câu V. (3,5 điểm)

Cho hình chóp tam giác đều S. ABC có các mặt là tam giác đều. Gọi O là trung điểm của đường cao SH của hình chóp.

Chứng minh rằng: góc AOB = BOC = COA = 90⁰

Đề thi học sinh giỏi môn Toán lớp 9

Bài 1: (2 điểm)

1. Cho biểu thức

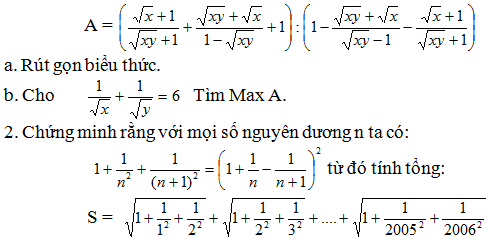
Bài 2 (2đ): Phân tích thành nhân tử: A = (xy + yz + zx) (x + y+ z) – xyz

Bài 3 (2đ):

1. Tìm giá trị của a để phương trình sau chỉ có 1 nghiệm:

Bài 6 (2đ): Trên mặt phẳng toạ độ cho đường thẳng (d) có phương trình: 2kx + (k – 1)y = 2 (k là tham số)

1. Tìm k để đường thẳng (d) song song với đường thẳng y = ? Khi đó hãy tính góc tạo bởi (d) và tia Ox.

2. Tìm k để khoảng cách từ gốc toạ độ đến đường thẳng (d) là lớn nhất?

Bài 7 (2đ): Giả sử x, y là các số dương thoả mãn đẳng thức: x + y = căn bậc 2 của 10

Tìm giá trị của x và y để biểu thức: P = (x⁴ + 1)(y⁴ + 1) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất ấy.

Bài 8 (2đ): Cho ABC với BC = 5cm, AC= 6cm; AB = 7cm. Gọi O là giao điểm 3 đường phân giác, G là trọng tâm của tam giác. Tính độ dài đoạn OG.

Bài 9 (2đ): Gọi M là một điểm bất kì trên đường thẳng AB. Vẽ về một phía của AB các hình vuông AMCD, BMEF.

a. Chứng minh rằng AE vuông góc với BC.

b. Gọi H là giao điểm của AE và BC. Chứng minh rằng ba điểm D, H, F thẳng hàng.

c. Chứng minh rằng đường thẳng DF luôn luôn đi qua một điểm cố định khi M chuyển động trên đoạn thẳng AB cố định.

d. Tìm tập hợp các trung điểm K của đoạn nối tâm hai hình vuông khi M chuyển động trên đường thẳng AB cố định.

Bài 10 (2đ): Cho $\widehat{x O y}$ $\widehat{x O y}$ khác góc bẹt và một điểm M thuộc miền trong của góc. Dựng đường thẳng qua M và cắt hai cạnh của góc thành một tam giác có diện tích nhỏ nhất.

Đề thi học sinh giỏi môn Toán lớp 9

Bài 1: (2 điểm)

Chứng minh:

$\sqrt[3]{\sqrt[3]{2}}-1=\sqrt[3]{\frac{1}{9}}-\sqrt[3]{\frac{2}{9}}+\sqrt[3]{\frac{4}{9}}$ $\sqrt[3]{\sqrt[3]{2}}-1=\sqrt[3]{\frac{1}{9}}-\sqrt[3]{\frac{2}{9}}+\sqrt[3]{\frac{4}{9}}$

Bài 2: (2 điểm)

Cho $4 a^{2}+b^{2}=5 \text { ab }(2 a>b>0)$ $4 a^{2}+b^{2}=5 \text { ab }(2 a>b>0)$

Tính số trị biểu thức: $\mathrm{M}=\frac{a b}{4 b^{2}-b^{2}}$ $\mathrm{M}=\frac{a b}{4 b^{2}-b^{2}}$

Bài 3: (2 điểm)

Chứng minh: nếu a, b là các nghiệm của phương trình: $\mathrm{x}^{2}+\mathrm{px}+1=0$ $\mathrm{x}^{2}+\mathrm{px}+1=0$ và c,d là các nghiệm của phương trình: $x^{2} + qx + 1 = 0$ $x^{2} + qx + 1 = 0$ thì ta có:

$\left(a–c\right)\left(b–c\right)\left(a + d\right)\left(b + d\right) = q^{2}–p^{2}$ $\left(a–c\right)\left(b–c\right)\left(a + d\right)\left(b + d\right) = q^{2}–p^{2}$

Bài 4: (2 điểm)

Giải bài toán bằng cách lập phương trình

Tuổi anh và em cộng lại bằng 21. Hiện tại tuổi anh gấp đôi tuổi em lúc anh bằng tuổi em hiện nay. Tính tuổi của anh, em.

Bài 5: (2 điểm)

Giải phương trình: $x^{4}+\sqrt{x^{2}+2006}=2006$ $x^{4}+\sqrt{x^{2}+2006}=2006$

Bài 6: (2 điểm)

Trong cùng một hệ trục toạ độ vuông góc, cho parapol $(\mathrm{P}): \mathrm{y}=-\frac{x^{2}}{4}$ $(\mathrm{P}): \mathrm{y}=-\frac{x^{2}}{4}$ và đường thẳng (d): y = mx – 2m – 1.

1. Vẽ (P)

2. Tìm m sao cho (d) tiếp xúc với (P)

3. Chứng tỏ (d) luôn đi qua điểm cố định A ∈ (P)

Bài 7: (2 điểm).

Cho biểu thức $A=x-2 \sqrt{x y}+3 y-2 \sqrt{x}+1$ $A=x-2 \sqrt{x y}+3 y-2 \sqrt{x}+1$

Tìm giá trị nhỏ nhất mà A có thể đạt được.

Bài 8: (4 điểm).

Cho hai đường tròn (O) và (O’) ở ngoài nhau. Kẻ tiếp tuyến chung ngoài AB và tiếp tuyến chung trong EF, A, E ∈ (O); B, F ∈ (O’)

a. Gọi M là giao điểm của AB và EF. Chứng minh: ∆ AOM ∾ ∆ BMO’

b. Chứng minh: AE ⊥ BF

c. Gọi N là giao điểm của AE và BF. Chứng minh: O,N,O’ thẳng hàng.

Tài liệu vẫn còn mời các bạn tải về để xem trọn nội dung

Trên đây VnDoc đã chia sẻ 40 đề luyện thi học sinh giỏi Toán 9. Tài liệu gồm 40 đề thi HSG lớp 9, đây là tài liệu hữu ích giúp các bạn học sinh ôn tập nâng cao kĩ năng giải đề thi, biết cách phân bổ thời gian làm bài. Chúc các bạn ôn thi tốt và cũng đừng quên thường xuyên tương tác với VnDoc.com để nhận rất nhiều tài liệu hay và hoàn toàn miễn phí nhé

.......................................................................

Ngoài 40 đề luyện thi học sinh giỏi Toán 9. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

215

114.243

Bài trước

Bài sau