Đề chọn học sinh giỏi tỉnh Toán THCS năm 2024 – 2025 sở GD&ĐT Vĩnh Long
Đề thi chọn HSG lớp 9 môn Toán
Lớp:
Lớp 9
Môn:
Toán
Dạng tài liệu:
Đề thi HSG
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Trang 1/2 - Môn Toán
28 10 3
3
x
x
x
x 5
H
4 m
O
K
F
D
6 m
SỞ GIÁO DỤC VÀ ĐÀO TẠO
VĨNH LONG
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH
NĂM HỌC 2024-2025
Khóa thi ngày 16.3.2025
ĐỀ CHÍNH THỨC
(Đề thi gồm 05 câu, 02 trang)
Môn thi: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Câu 1. (5.0 điểm)
a) Tính giá trị của biểu thức A
.
b) Cho biểu thức B
x 3
x 1
x 7
x
với x 0,x 1, x 9 .
1 3
x 4
3
:
1
x 1
Rút gọn biểu thức B và tìm các giá trị nguyên của x để B nhận giá trị nguyên.
c) Tìm giá trị nhỏ nhất của biểu thức C 5x
2
5x 20 .
Câu 2. (7.0 điểm)
a) Giải phương trình x
2
7x 30 6 .
b) Giải hệ phương trình
x
2
2y 3 y
2
4x
x
2
y
2
5
.
c) Cho phương trình x
2
2x 1 0 có hai nghiệm x và x . Không giải phương trình,
1 2
x
3
x
3
2
hãy tính giá trị của biểu thức M
1
2
.
x
4
x
4
2 1
d) Đến kỷ niệm ngày Quốc tế Phụ nữ 8-3, một cửa hàng hoa ở Vĩnh Long đã nhập 500
giỏ hoa hồng từ Đà Lạt về để bán. Các giỏ hoa hồng được chuyển về đến cửa hàng vào
sáng ngày 07/3/2025. Cửa hàng treo giá niêm yết bán một giỏ hoa hồng tăng 25% so với
giá lúc nhập về. Đến hết ngày 08/3/2025, cửa hàng bán được 400 giỏ hoa hồng. Đến ngày
09/3/2025, cửa hàng treo bảng giá mới (giảm 50% so với giá lúc nhập về) và đã bán hết số
giỏ hoa hồng còn lại. Hỏi giá một giỏ hoa hồng lúc cửa hàng nhập về là bao nhiêu? Biết
cửa hàng khi bán hết 500 giỏ hoa hồng thì lãi được 10 000 000 đồng.
Câu 3. (1.0 điểm)
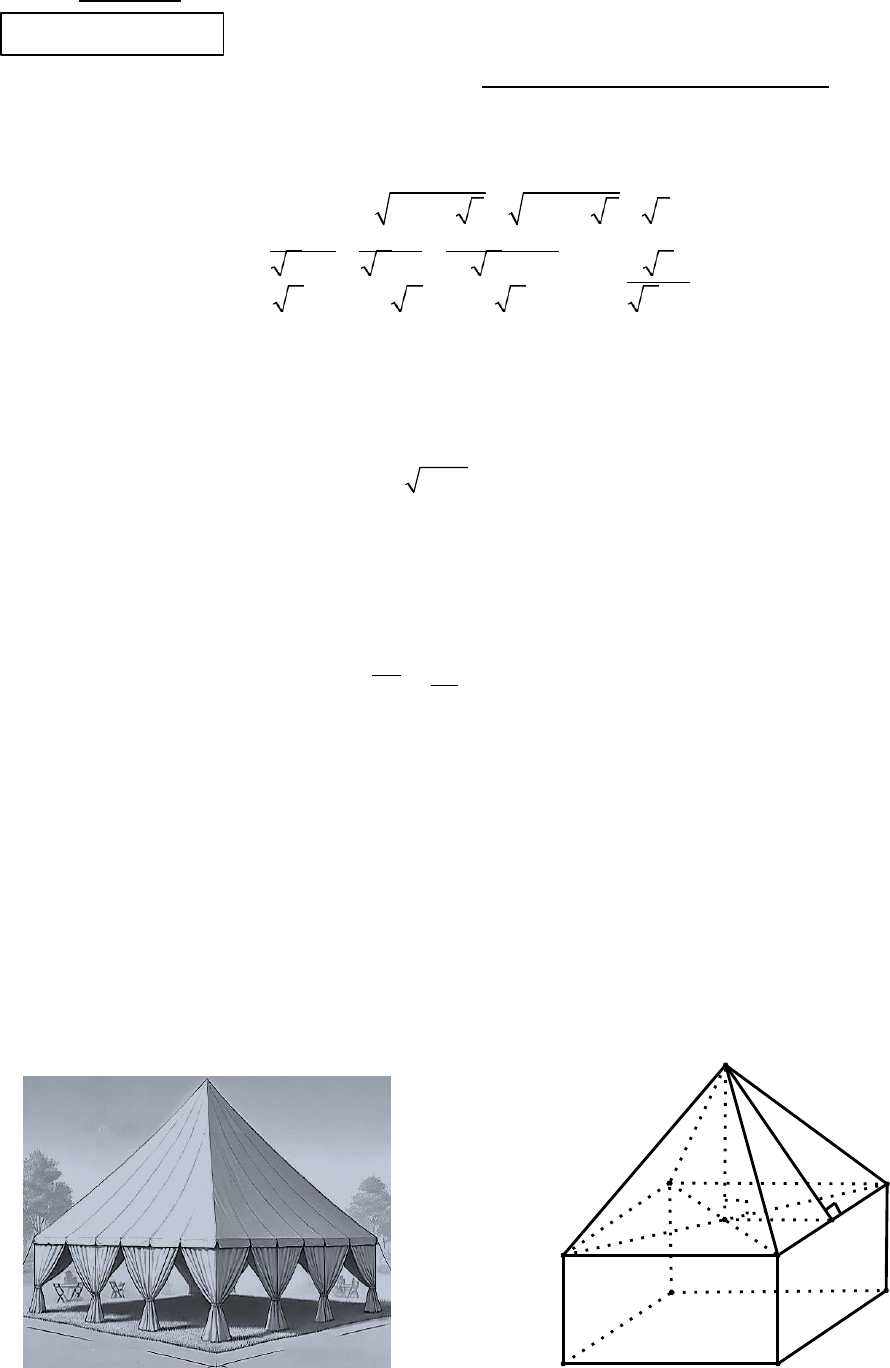
Một chiếc lều có dạng như hình vẽ bên dưới.
S
G
E
3 m
C
A
B
2112 3

Trang 2/2 - Môn Toán
Biết phần thân lều dạng hình hộp chữ nhật ABCD.EFGH, mặt đáy là hình vuông cạnh
6m, chiều cao 3m. Phần nóc lều dạng hình chóp tứ giác đều S.EFGH có chiều cao 4m.
a) Tính thể tích không khí bên trong chiếc lều.
b) Tính chi phí để mua vải bạt phủ nóc lều (không tính các mép dán), biết mỗi mét
vuông vải bạt có giá 20 000 đồng và SO OK .
Câu 4. (4.0 điểm)
Cho đường tròn
O
có hai đường kính AB và CD vuông góc với nhau. Lấy điểm E
thuộc cung nhỏ CB ( E khác C và B ). Gọi F là giao điểm của hai đường thẳng AC và
BE . Kẻ CH vuông góc với BF
H BF
, BC cắt OH tại I . Chứng minh rằng:
a)
Bốn điểm
C, H, B, O
cùng nằm trên một đường tròn và
HO
là tia phân giác của
C
‸
HB
.
b) CI.CH HF.BI .
c) Ba điểm F, I, D thẳng hàng.
Câu 5. (3.0 điểm)
2 3
a) Chứng minh rằng biểu thức D
n
n
n
luôn nhận giá trị nguyên với mọi n là
12 8 24
số nguyên chẵn.
b) Cho a, b, c là các số thực dương. Chứng minh rằng
ab
bc
ca
1
a b c
.
a b 2c b c 2a c a 2b 4
- HẾT -
- Thí sinh không được sử dụng máy tính cầm tay và tài liệu.
- Giám thị không giải thích gì thêm.
Họ và tên thí sinh:................................................................. Số báo danh:........................

Trang 1/6
28 10 3
3
x
x
x
: 1
SỞ GIÁO DỤC ĐÀO TẠO
VĨNH LONG
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH
NĂM HỌC 2024-2025
Khóa thi ngày: 16.3.2025
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC
Môn: TOÁN
(Hướng dẫn chấm có 06 trang)
Câu 1. (5.0 điểm)
a) Tính giá trị của biểu thức A
.
b) Cho biểu thức B
x 3
x 1
x 7
x
với x 0,x 1, x 9 .
1 3 x 4
3
x 1
Rút gọn biểu thức B và tìm các giá trị nguyên của x để B nhận giá trị nguyên.
c) Tìm giá trị nhỏ nhất của biểu thức C 5x
2
5x 20 .
Câu
Điểm
1
5.0
a) Ta có
2112 3
2 3 3
2
0.5
2
3 3
0.25
28 10
3
5
3
2
0.5
5 3
0.25
A 2
3 3 5 3 3
0.25
A 8
0.25
b) B
x 3
x 1
x 7
:
1
x
x 1 3 x x 4
x 3
x 1
x 3
x 3
x 1
x 1
x 7
:
x 1 x
x 1
x 3
x
1
0.5
x 9 x 1 x 7 x 1
x 1
x 1
x 1
x 3
.
1
x 1
x 3
0.25
x 1
x 3
0.25
Ta có
x 1
1
4
x 3 x 3
0.25
Để B nhận giá trị nguyên khi x 3Ư(4)
1; 2; 4
0.25
Khi đó x 3 1 suy ra x 16 (nhận)
x 3 1 suy ra x 4 (nhận)
x 3 2 suy ra x 25 (nhận)
x 3 2 suy ra x 1 (loại)
0.5
2112 3
Đề chọn học sinh giỏi tỉnh Toán THCS năm 2024 – 2025 sở GD&ĐT Vĩnh Long được thiết kế bám sát chương trình, giúp học sinh phát triển tư duy và kỹ năng giải toán nâng cao.
Bài viết này cung cấp đề thi chính thức, đáp án chi tiết và hướng dẫn giải các bài toán tiêu biểu. Đây là tài liệu tham khảo quý giá giúp giáo viên tham khảo ra đề, ôn luyện có định hướng cho học sinh và chuẩn bị đội tuyển học sinh giỏi tỉnh hiệu quả.




