Chứng minh đường thẳng đi qua điểm cố định

Trong các đề thi học sinh giỏi, thi vào trư­ờng chuyên, lớp chọn thư­ờng có những bài toán liên quan đến tìm điểm cố định, chứng minh đư­ờng đi qua điểm cố định. Thực tế cho thấy đây là bài toán khó, học sinh thường khó khăn khi gặp phải bài toán dạng này.

A. Cách chứng minh đường thẳng đi qua điểm cố định

Bài toán “Đường đi qua điểm cố định” đòi hỏi HS phải có kĩ năng nhất định cộng với sự đầu tư­ suy nghĩ, tìm tòi nhưng đặc biệt phải có phương pháp làm bài.

Tìm hiểu nội dung bài toán

Dự đoán điểm cố định

Tìm tòi hư­ớng giải

Trình bày lời giải

Tìm hiểu bài toán:

Yếu tố cố định. (điểm, đư­ờng … )

Yếu tố chuyển động. (điểm, đư­ờng … )

Yếu tố không đổi. (độ dài đoạn, độ lớn góc … )

Quan hệ không đổi (Song song, vuông góc, thẳng hàng … )

Khâu tìm hiểu nội dung bài toán là rất quan trọng. Nó định hư­ớng cho các thao tác tiếp theo. Trong khâu này đòi hỏi học sinh phải có trình độ phân tích bài toán, khả năng phán đoán tốt. Tuỳ thuộc vào khả năng của từng đối tư­ợng học sinh mà giáo viên có thể đ­ưa ra hệ thống câu hỏi dẫn dắt thích hợp nhằm giúp học sinh tìm hiểu tốt nội dung bài toán. Cần xác định rõ yếu tố cố định, không đổi, các quan hệ không đổi và các yếu tố thay đổi, tìm mối quan hệ giữa các yếu tố đó.

Dự đoán điểm cố định:

Dựa vào những vị trí đặc biệt của yếu tố chuyển động để dự đoán điểm cố định. Thông th­ường ta tìm một hoặc hai vị trí đặc biệt cộng thêm với các đặc điểm bất biến khác nh­ư tính chất đối xứng, song song, thẳng hàng … để dự đoán điểm cố định

Tìm tòi h­ướng giải

Từ việc dự đoán điểm cố định tìm mối quan hệ giữa điểm đó với các yếu tố chuyển động, yếu tố cố định và yếu tố không đổi. Thông thư­ờng để chứng tỏ một điểm là cố định ta chỉ ra điểm đó thuộc hai đ­ường cố định, thuộc một đường cố định và thoả mãn một điều kiện (thuộc một tia và cách gốc một đoạn không đổi, thuộc một đ­ường tròn và là mút của một cung không đổi ...) thông thư­ờng lời giải của một bài toán th­ường đư­ợc cắt bỏ những suy nghĩ bên trong nó chính vì vậy ta thư­ờng có cảm giác lời giải có cái gì đó thiếu tự nhiên, không có tính thuyết phục chính vì vậy khi trình bày ta cố gắng làm cho lời giải mang tính tự nhiên hơn, có giá trị về việc rèn luyện tư­ duy cho học sinh.

B. Bài tập chứng minh đường thẳng đi qua điểm cố định

Bài 1: Cho ba điểm A, C, B thẳng hành theo thứ tự đó. Vẽ tia Cx vuông góc với AB.Trên tia Cx lấy hai điểm D, E sao cho \(\frac{CE}{CB} = \frac{CA}{CD} = \sqrt{3}\). Đường tròn ngoại tiếp tam giác ADC cắt đường tròn ngoại tiếp tam giác BEC tại H khác C. Chứng minh rằng: Đường thẳng HC luôn đi qua một điểm cố định khi C di chuyển trên đoạn thẳng AB.

Hình vẽ minh họa

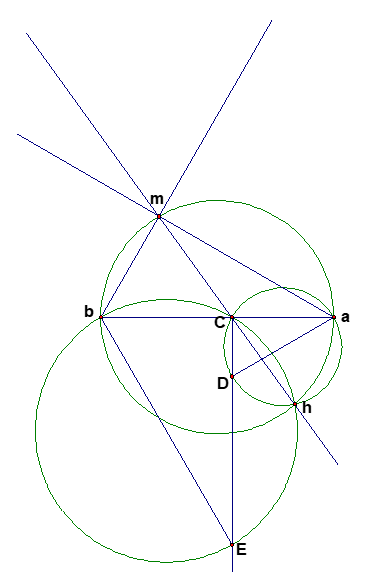
Tìm hiểu đề bài:

* Yếu tố cố định: Đoạn AB

* Yếu tố không đổi:

+ Góc BEC = 30⁰, Góc ADB = 60⁰ do đó sđ cung BC, cung CA không đổi

+ B, D, H thẳng hàng; E, H, A thẳng hàng

Dự đoán điểm cố định:

Khi C trùng B thì (d) tạo với BA một góc 60⁰ => điểm cố định thuộc tia By tạo với tia BA một góc 60⁰

Khi C trùng A thì (d) tạo với AB một góc 30⁰ => điểm cố định thuộc tia Az tạo với tia AB một góc 30⁰

By và Az cắt nhau tại M thì M là điểm cố định? Nhận thấy M nhìn AB cố định dưới 90⁰ => M thuộc đường tròn đường kính AB.

Tìm hướng chứng minh:

M thuộc đường tròn đường kính AB cố định do đó cần chứng minh sđ cung AM không đổi thật vậy:

Sđ cung AM \(= \ 2sd\widehat{MCA} = 2sd\widehat{CHA} = 2sd\widehat{CDA} = 120^{0}\)

Hướng dẫn giải

Ta có \(\tan D = \frac{CA}{CD} = \sqrt{3} \Rightarrow \widehat{D} = 60^{0}\)

Lại có: \(\widehat{CHA\ } = \widehat{CDA} = 60^{0}\)

Gỉa sử đường tròn đường kính AB cắt CH tại M

Ta có; \(\widehat{MHA} = 60^{0} = >\) Số đo cung MA không đổi

Lại có đường tròn đường kính AB cố định

Vậy M cố định. Do đó CH luôn qua M cố định.

Bài 2: Cho đường tròn (O) và đường thẳng (d) nằm ngoài đường tròn. I là điểm di động trên (d). Đường tròn đường kính OI cắt (O) tại M, N. Chứng minh đường tròn đường kính OI luôn đi qua một điểm cố định khác O và đường thẳng MN luôn đi qua một điểm cố định.

Hình vẽ minh họa

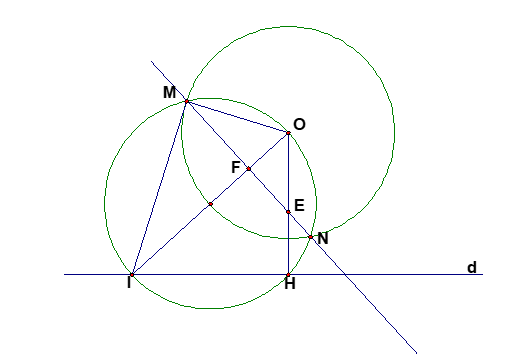
Tìm hướng chứng minh

Do tính chất đối xứng nên điểm cố định nằm trên trục đối xứng hay đường thẳng qua O và vuông góc với (d).

Hướng dẫn giải

Kẻ OH vuông góc với (d) cắt MN tại E.

ta có H cố định và H thuộc đường tròn đường kính OI vậy đường tròn đường kính OI luôn đi qua K cố định.

Xét tam giác OEF và tam giác OIH có góc O chung, \(\widehat{OFE} = \widehat{OHI} = 90^{0}\)

Nên tam giác OEF đồng dạng với tam giác OIH do đó:

\(\frac{OF}{OE} = \frac{OH}{OI} \Rightarrow OE.OH = OF.\ OI\)

Lại có \(\widehat{IMO} = 90^{0}\) (nội tiếp chắn nửa đường tròn đường kính OI )

Xét tam giác vuông OMI có đường cao ứng với cạnh huyền MF nên: \(OF.\ OI = OM^{2}\)

Do đó: \(OE = \frac{OM^{2}}{OH}\)= Hằng số

Vậy E cố định do đó MN đi qua E cố định.

Bài 3: Cho đường tròn (O; R) và dây AB cố định. C là một điểm chuyển động trên đường tròn và M là trung điểm của AC. Chứng minh rằng đường thẳng kẻ từ M vuông góc với BC luôn đi qua một điểm cố định.

Hình vẽ minh họa

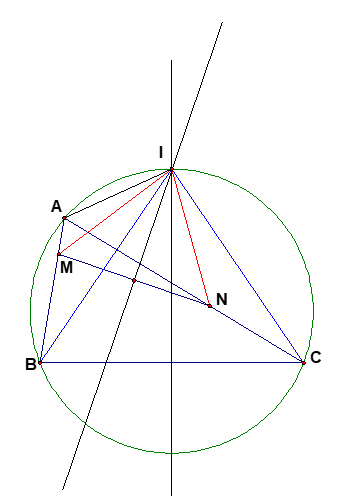
Hướng dẫn giải

Vẽ đường kính BD => D cố định.

Giả sử đường thẳng qua M và vuông góc với BC cắt BC cắt AD tại I.

Dễ thấy \(\widehat{BCD} = 90^{0}\) hay MI // CD.

Xét tam giác ACD có MC = MA; MI // CD

=> I là trung điểm của DA cố định hay đường thẳng qua M vuông góc với BC đi qua I cố định.

C. Bài tập tự rèn luyện chứng minh

Bài 1: Cho tam giác ABC và hai điểm M, N thứ tự chuyển động trên hai tia BA, CA sao cho BM = CN. Chứng minh rằng đường trung trực của MN luôn đi qua một điểm cố định.

Bài 2: Cho đường tròn (O; R) và dây cung AB = R\(\sqrt{3}\). Điểm P khác A và B. Gọi (C; R₁) là đường tròn đi qua P tiếp xúc với đường tròn (O; R) tại A. Gọi (D; R₂) là đường tròn đi qua P tiếp xúc với đường tròn (O; R) tại B. Các đường tròn (C; R₁) và (D; R₂) cắt nhau tại M khác P. Chứng minh rằng khi P di động trên AB thì đường thẳng PM luôn đi qua một điểm cố định.

Bài 3: Cho đoạn AB cố định, M di động trên AB. Trên cùng một nửa mặt phẳng bờ AB vẽ hai hình vuông MADE và MBHG. Hai đường tròn ngoại tiếp hai hình vuông cắt nhau tại N. Chứng minh đường thẳng MN luôn đi qua một điểm cố định khi M di chuyển trên AB.

-----------------------------------------

Mời bạn đọc tải tài liệu tham khảo đầy đủ!