VnDoc.com

Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng

Bồi dưỡng HSG lớp 9 môn Toán

Tải về

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Đề thi HSG

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

NHỮNG ĐỊNH LÝ HÌNH HỌC NỔI TIẾNG - Toán lớp 9

1. Đường thẳng Euler

1.(Đường thẳng Euler). Cho tam giác

ABC

. Chứng minh rằng trọng tâm

G

, trực

tâm

H

và tâm đường tròn ngoại tiếp

O

cùng nằm trên một đường thẳng. Hơn nữa

2

GH

GO

=

. Đường thẳng nối

, ,H G O

gọi là đường thẳng Euler của tam giác

ABC

.

Chứng minh:

Cách 1: Gọi

,E F

lần lượt là trung điểm của

,BC AC

. Ta có

EF

là đường

trung bình của tam giác

ABC

nên

/ /EF AB

. Ta lại có

/ /OF BH

(cùng

vuông góc với

AC

). Do đó

·

OFE ABH=

(góc có cạnh tương ứng song song).

Chứng minh tương tự

·

OEF BAH=

.

Từ đó có

ABH EFOD D:

(g.g)

2

AH AB

OE EF

Þ = =

(do

EF

là đường trung

bình của tam giác

ABC

). Mặt khác

G

là trọng tâm của tam giác

ABC

nên

2

AG

GE

=

. Do đó

2

AG AH

FG OE

= =

, lại có

·

HAG OEG=

(so le trong,

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

/ /OE AH

)

HA G EOGÞ D D:

(c.g.c)

·

HGA EGOÞ =

. Do

·

0

180EGO AGO+ =

nên

·

0

180HGA AGO+ =

hay

·

0

180HGO =

.

Vậy

, ,H G O

thẳng hàng.

Cách 2: Kẻ đường kính

AD

của đường tròn

( )O

ta có

BH AC^

(Tính chất

trực tâm)

AC CD^

(Góc nội tiếp chắn nửa đường tròn) suy ra

/ /BH CD

.

Tương tự ta cũng có

/ /CH BD

nên tứ giác

BHCD

là hình bình hành, do đó

HD

cắt

BC

tại trung điểm của mỗi đường. Từ đó cũng suy ra

1

/ /

2

OM AH=

(Tính chất đường trung bình tam giác

ADH

). Nối

AM

cắt

HO

tại

G

thì

1

2

GO OM

GH A H

= =

nên

G

là trọng tâm của tam giác

ABC

.

Cách 3: sử dụng định lý Thales :Trên tia đối

GO

lấy

'H

sao cho

' 2GH GO=

. Gọi

M

là trung điểm

BC

. Theo tính chất trọng

tâm thì

G

thuộc

AM

và

2GA GM=

.

Áp dụng định lý Thales

vào tam giác

GOM

dễ suy ra

'/ /AH OM

(1).Mặt khác do

O

là tâm đường tròn ngoại tiếp tam giác

ABC

,

M

là trung điểm

BC

nên

OM BC^

(2).

Từ (1) và (2) suy ra

'A H BC^

, tương tự

'BH CA^

. Vậy

'H Hº

là trực

tâm tam giác

ABC

. Theo cách dựng

'H

ta có ngay kết luận bài toán.

Chú ý rằng: Nếu ta kéo dài

AH

cắt đường tròn tại

H'

thì





0

AH' D 90

(Góc

nội tiếp chắn nữa đường tròn) nên

EM

là đường trung bình của tam giác

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

HH' D

suy ra

H

đối xứng với

H'

qua

BC

. Nếu gọi

O'

là tâm vòng tròn ngoại

tiếp tam giác

HBC

thì ta có

O'

đối xứng với

O

qua

BC

.

Đường thẳng đi qua

H,G,O

được gọi là đường thẳng Euler của tam giác

ABC

. Ngoài ra ta còn có

OH 3OG

.

*Đường thẳng Euler có thể coi là một trong những định lý quen thuộc nhất của

hình học phẳng. Khái niệm đường thẳng Euler trước hết liên quan đến tam giác,

sau đó được mở rộng và ứng dụng cho tứ giác nội tiếp và cả

n

- giác nội tiếp,

trong chuyên đề ta quan tâm đến một số vấn đề có liên quan đến khái niệm

này trong tam giác.

1.1. (Mở rộng đường thẳng Euler) Cho tam giác

ABC

.

P

là điểm bất kỳ

trong mặt phẳng. Gọi

', ', 'A B C

lần lượt là trung điểm của

, ,BC CA AB

.

G

là trọng tâm tam giác

ABC

.

a) Chứng minh rằng các đường thẳng qua

, ,A B C

lần lượt song song với

', ', 'PA PB PC

đồng quy tại một điểm

P

H

, hơn nữa

, ,

P

H G P

thẳng hàng

và

2

P

GH

GP

=

.

b) Chứng minh rằng các đường thẳng qua

', ', 'A B C

lần lượt song song với

, ,PA PB PC

đồng quy tại một điểm

P

O

, hơn nữa

, ,

P

O G P

thẳng hàng và

1

2

P

GO

GP

=

.

Giải:

a) Ta thấy rằng kết luận của bài toán khá rắc rối, tuy nhiên ý tưởng của lời giải

câu 1 giúp ta tìm đến một lời giải rất ngắn gọn như sau:

Lấy điểm

Q

trên tia đối tia

GP

sao

cho

2GQ GP=

. Theo tính chất trọng

Chuyên đề 6: Những Định lý Hình học nổi tiếng

VnDoc xin giới thiệu Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng. Tài liệu giúp các bạn học sinh củng cố lại phần kiến thức đã học và kỹ năng giải bài tập, biết cách phân bổ thời gian làm bài sao cho hợp lý. Mời các bạn cùng tham khảo

Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng được VnDoc đã chia sẻ trên đây. Nội dung gồm lý thuyết và các câu hỏi bài tập trong chuyên đề về Những Định lý Hình học nổi tiếng, chuẩn bị tốt cho kì thi HSG lớp 9 sắp tới. Chúc các bạn học tốt, mời các bạn tham khảo

Đường thẳng Euler

1.(Đường thẳng Euler). Cho tam giác $ABC$ . Chứng minh rằng trọng tâm $G$ , trực tâm $H$ và tâm đường tròn ngoại tiếp $O$ cùng nằm trên một đường thẳng. Hơn nữa $\frac{GH}{GO} = 2$ . Đường thẳng nối $H,G,O$ gọi là đường thẳng Euler của tam giác $ABC$ .

Chứng minh:

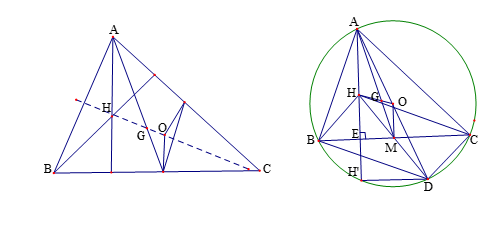
Cách 1: Gọi $E,F$ lần lượt là trung điểm của $BC,AC$ . Ta có $EF$ là đường trung bình của tam giác $ABC$ nên $EF//AB$ .

Ta lại có $OF//BH$ (cùng vuông góc với $AC$ ). Do đó $\widehat{OFE} = \widehat{ABH}$ (góc có cạnh tương ứng song song). Chứng minh tương tự $\widehat{OEF} = \widehat{BAH}$ .

Từ đó có $\Delta ABH\sim\Delta EFO$ (g.g) $\Rightarrow \frac{AH}{OE} = \frac{AB}{EF} = 2$ (do $EF$ là đường trung bình của tam giác $ABC$ ). Mặt khác $G$ là trọng tâm của tam giác $ABC$ nên $\frac{AG}{GE} = 2$ .

Do đó $\frac{AG}{FG} = \frac{AH}{OE} = 2$ , lại có $\widehat{HAG} = \widehat{OEG}$ (so le trong, $OE//AH$ ) $\Rightarrow \Delta HAG\sim\Delta EOG$ (c.g.c) $\Rightarrow \widehat{HGA} = \widehat{EGO}$ . Do $\widehat{EGO} + \widehat{AGO} = 180^{0}$ nên $\widehat{HGA} + \widehat{AGO} = 180^{0}$ hay $\widehat{HGO} = 180^{0}$ .

Vậy $H,G,O$ thẳng hàng.

Cách 2: Kẻ đường kính $AD$ của đường tròn $(O)$ ta có $BH\bot AC$ (Tính chất trực tâm) $AC\bot CD$ (Góc nội tiếp chắn nửa đường tròn) suy ra $BH//CD$ . Tương tự ta cũng có $CH//BD$ nên tứ giác $BHCD$ là hình bình hành, do đó $HD$ cắt $BC$ tại trung điểm của mỗi đường.

Từ đó cũng suy ra $OM// = \frac{1}{2}AH$ (Tính chất đường trung bình tam giác $ADH$ ). Nối $AM$ cắt $HO$ tại $G$ thì $\frac{GO}{GH} = \frac{OM}{AH} = \frac{1}{2}$ nên $G$ là trọng tâm của tam giác $ABC$ .

Cách 3: sử dụng định lý Thales: Trên tia đối $GO$ lấy $H'$ sao cho $GH' = 2GO$ . Gọi $M$ là trung điểm $BC$ . Theo tính chất trọng tâm thì $G$ thuộc $AM$ và $GA = 2GM$ .

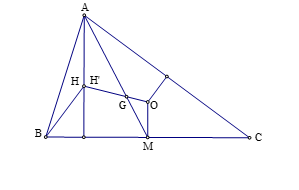
Áp dụng định lý Thales vào tam giác $GOM$ dễ suy ra $AH'//OM$ (1). Mặt khác do $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$ , $M$ là trung điểm $BC$ nên $OM\bot BC$ (2).

Từ (1) và (2) suy ra $AH'\bot BC$ , tương tự $BH'\bot CA$ . Vậy $H' \equiv H$ là trực tâm tam giác $ABC$ . Theo cách dựng $H'$ ta có ngay kết luận bài toán.

Chú ý rằng: Nếu ta kéo dài $AH$ cắt đường tròn tại $H'$ thì $\widehat{AH'D} = 90^{0}$ (Góc nội tiếp chắn nữa đường tròn) nên $EM$ là đường trung bình của tam giác $HH'D$ suy ra $H$ đối xứng với $H'$ qua $BC$ . Nếu gọi $O'$ là tâm vòng tròn ngoại tiếp tam giác $HBC$ thì ta có $O'$ đối xứng với $O$ qua $BC$ .

Đường thẳng đi qua $H,G,O$ được gọi là đường thẳng Euler của tam giác $ABC$ . Ngoài ra ta còn có $OH = 3OG$ .

Đường thẳng Euler có thể coi là một trong những định lý quen thuộc nhất của hình học phẳng. Khái niệm đường thẳng Euler trước hết liên quan đến tam giác, sau đó được mở rộng và ứng dụng cho tứ giác nội tiếp và cả $n$ - giác nội tiếp, trong chuyên đề ta quan tâm đến một số vấn đề có liên quan đến khái niệm này trong tam giác.

Mở rộng đường thẳng Euler

Cho tam giác $ABC$ . $P$ là điểm bất kỳ trong mặt phẳng. Gọi $A',B',C'$ lần lượt là trung điểm của $BC,CA,AB$ . $G$ là trọng tâm tam giác $ABC$ .

a) Chứng minh rằng các đường thẳng qua $A,B,C$ lần lượt song song với $PA',PB',PC'$ đồng quy tại một điểm $H_{P}$ , hơn nữa $H_{P},G,P$ thẳng hàng và $\frac{GH_{P}}{GP} = 2$ .

b) Chứng minh rằng các đường thẳng qua $A',B',C'$ lần lượt song song với $PA,PB,PC$ đồng quy tại một điểm $O_{P}$ , hơn nữa $O_{P},G,P$ thẳng hàng và $\frac{GO_{P}}{GP} = \frac{1}{2}$ .

Giải:

Hình vẽ minh họa:

a) Ta thấy rằng kết luận của bài toán khá rắc rối, tuy nhiên ý tưởng của lời giải câu 1 giúp ta tìm đến một lời giải rất ngắn gọn như sau:

Lấy điểm $Q$ trên tia đối tia $GP$ sao cho $GQ = 2GP$ . Theo tính chất trọng tâm ta thấy ngay $G$ thuộc $AA'$ và $GA = 2GA'$ . Vậy áp dụng định lý

Thales vào tam giác $GPA'$ dễ suy ra $AQ//PA'$ . Chứng minh tương tự $BQ//PB',CQ//PC'$ . Như vậy các

đường thẳng qua $A,B,C$ lần lượt song song với $PA',PB',PC'$ đồng quy tại $Q \equiv H_{P}$ . Hơn nữa theo cách dựng $Q$ thì $H_{P},G,O$ thẳng hàng và $\frac{GH_{P}}{GO} = 2$ . Ta có ngay các kết luận bài toán.

b) Ta có một lời giải tương tự. Lấy điểm $R$ trên tia đối tia $GP$ sao cho $GR = \frac{1}{2}GP$ .

Theo tính chất trọng tâm ta thấy ngay $G$ thuộc $AA'$ và $GA = 2GA'$ .

Vậy áp dụng định lý Thales vào tam giác $GPA$ dễ suy ra $AR//PA$ . Chứng minh tương tự $BR//PB,CR//PC$ . Như vậy các đường thẳng qua $A,B,C$ lần lượt song song với $PA,PB,PC$ đồng quy tại $R \equiv O_{P}$ . Hơn nữa theo cách dựng $R$ thì $O_{P},G,P$ thẳng hàng và $\frac{GP}{GO_{P}} = 2$ . Ta có ngay các kết luận bài toán.

Nhận xét: Bài toán trên thực sự là mở rộng của đường thẳng Euler.

Phần a) Khi $P \equiv O$ tâm đường tròn ngoại tiếp của tam giác $ABC$ ta có ngay $H_{P} = H$ là trực tâm của tam giác $ABC$ . Ta thu dược nội dung của bài toán đường thẳng Euler.

Phần b) Khi $P \equiv H$ trực tâm của tam giác $ABC$ thì $O_{P} \equiv O$ tâm đường tròn ngoại tiếp tam giác $ABC$ .

1.2. Cho tam giác $ABC$ trực tâm $H$ . Khi đó đường thẳng Euler của các tam giác $HBC,BCHCA,HAB$ đồng quy tại một điểm trên đường thẳng Euler của tam giác $ABC$ .

Giải:

Để giải bài toán này chúng ta cần hai bổ đề quen thuộc sau:

Bổ đề 1. Cho tam giác $ABC$ trực tâm $H$ . Thì $(HBC),(HCA),(HAB)$ lần lượt đối xứng với $(ABC)$ qua $BC,CA,AB$ .

Chứng minh: Gọi giao điểm khác $A$ của $HA$ với $(ABC)$ là $A'$ . Theo tính chất

trực tâm và góc nội tiếp dễ thấy $\widehat{HBC} = \widehat{HAC} = \widehat{A'BC}$ . Do đó tam giác

$HBA'$ cân tại $B$ hay $H$ và $A'$ đối xứngnhau qua $BC$ do đó $(HBC)$ đối xứng $(ABC)$ .

Tương tự cho $(HCA),(HAB)$ , ta có điều phải chứng minh.

Bổ đề 2. Cho tam giác $ABC$ , trực tâm $H$ , tâm đường tròn ngoại tiếp $O$ , $M$ là trung điểm thì $HA = 2OM$ .

Chứng minh:

Gọi $N$ là trung điểm của $CA$ dễ thấy $OM//HA$ do cùng vuông góc với $BC$

và $OM//HB$ do cùng vuông góc với $CA$ nên ta có tam giác $\Delta HAB\sim\Delta OMN$

tỷ số $\frac{AB}{MN} = 2$ . Do đó $HA = 2OM$ , đó là điều phải chứng minh.

Trở lại bài toán. Gọi $O_{A}$ là tâm $(HBC)$ theo bổ đề 5.1 thì $O_{A}$ đối xứng với $O$

qua $BC$ ,kết hợp với bổ đề 2 suy ra $OO_{A}$ song song và bằng $OH$ nên tứ giác $AHO_{A}A$ là hình bình hành nên $AO_{A}$ đi qua trung điểm $E$ của $OH$ .

Tuy nhiên dễ thấy $A$ là trực tâm tam giác $HBC$ do đó đường thẳng Euler của tam giác $HBC$ là $AO_{A}$ đi qua $E$ . Tương tự thì đường thẳng Euler của các tam giác $HCA,HAB$ cũngđi qua $E$ nằm trên $OH$ là đường thẳng Euler của tam giác $ABC$ . Đó là điều phải chứng minh.

Nhận xét: Điểm đồng quy $E$ là trung điểm $OH$ cũng chính là tâm đường tròn Euler của tam giác $ABC$

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

----------------------------------------------------------------------------

Ngoài Bồi dưỡng HSG Toán 9 chuyên đề 6: Những Định lý Hình học nổi tiếng. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 9, đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2026 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Tải về

Chọn file muốn tải về: