Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 9 Thi học sinh giỏi lớp 9 Toán 9

Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

Bồi dưỡng HSG lớp 9 môn Toán
Lớp: Lớp 9
Môn: Toán
Dạng tài liệu: Đề thi HSG
Loại File: Word + PDF
Phân loại: Tài liệu Tính phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
Toán lớp 9: CHƯƠNG 2: ĐƯỜNG TRÒN
CHỦ ĐỀ 1: SỰ XÁC ĐỊNH CỦA ĐƯỜNG TRÒN
Định nghĩa: Đường tròn tâm
O
bán kính
R 0
là hình gồm các điểm cách
điểm
O
một khoảng
R
kí hiệu là
(O; R)
hay
(O)
+ Đường tròn đi qua các điểm
1 2 n
A ,A ,...,A
gọi là đường tròn ngoại tiếp đa
giác
1 2 n
A A ...A
+ Đường tròn tiếp xúc với tất cả các cạnh của đa giác
1 2 n
A A ...A
gọi là
đường tròn nội tiếp đa giác đó.
Những tính chất đặc biệt cần nhớ:
+ Trong tam giác vuông trung điểm cạnh huyền là tâm vòng tròn ngoại tiếp
+ Trong tam giác đều , tâm vòng tròn ngoại tiếp là trọng tâm tam giác đó.
+ Trong tam giác thường:
Tâm vòng tròn ngoại tiếp là giao điểm của 3 đường trung trực của 3 cạnh
tam giác đó
Tâm vòng tròn nội tiếp là giao điểm 3 đường phân giác trong của tam giác
đó
PHƯƠNG PHÁP: Để chứng minh các điểm
1 2 n
A ,A ,...,A
cùng thuộc một
đường tròn ta chứng minh các điểm
1 2 n
A ,A ,...,A
cách đều điểm
O
cho
trước.
Ví dụ 1) Cho tam giác đều
có cạnh bằng
a
.
AM, BN,CP
là các đường
trung tuyến. Chứng minh 4 điểm
B,P,N,C
cùng thuộc một đường tròn. Tính
bán kính đường tròn đó.
Giải:
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
Vì tam giác
đều nên các trung tuyến đồng thời cũng là đường cao .
Suy ra
AM, BN,CP
lần lượt vuông góc với
BC,AC,AB
.
Từ đó ta có các tam giác
BPC,BNC
là tam giác vuông
Với
BC
là cạnh huyền, suy ra
MP MN MB MC
Hay: Các điểm
B,P,N,C
cùng thuộc đường tròn
Đường kính
BC a
, tâm đường tròn là
Trung điểm
M
của
BC
Ví dụ 2) Cho tứ giác
ABCD
có
0
C D 90 .
Gọi
M,N,P,Q
lần lượt là trung
điểm của
AB, BD,DC,CA
. Chứng minh 4 điểm
M,N,P,Q
cùng thuộc một
đường tròn. Tìm tâm đường tròn đó .
Giải:
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
Kéo dài
AD,CB
cắt nhau tại điểm
T
thì tam giác
vuông tại
T
.
+ Do
MN
là đường trung bình của tam giác
ABD
nên
NM / /AD
+
MQ
là đường trung bình của tam giác
nên
MQ / /BC
. Mặt khác
AD BC MN MQ
. Chứng minh tương tự ta cũng có:
MN NP,NP PQ
. Suy ra
MNPQ
là hình chữ nhật.
Hay các điểm
M,N,P,Q
thuộc một đường tròn có tâm là giao điểm
O
của
hai đường chéo
NQ,MP
Ví dụ 3) Cho tam giác
cân tại
A
nội tiếp đường tròn
(O)
. Gọi
M
là
trung điểm của
AC
G
là trọng tâm của tam giác
ABM
. Gọi
Q
là giao điểm của
BM
và
GO
.
Xác định tâm đường tròn ngoại tiếp tam giác
BGQ
.
Giải:
Vì tam giác
cân tại
A
nên tâm
O
của vòng tròn ngoại tiếp tam giác
nằm trên đường trung trực của
BC
.Gọi
K
là giao điểm của
AO
và
BM
Dưng các đường trung tuyến
MN, BP
của tam giác
ABM
cắt nhau tại trọng
tâm
G
.Do
MN / /BC MN AO
. Gọi
K
là giao điểm của
BM
và
AO
thì
K
là trọng tâm của tam giác
suy ra
GK / /AC
.

VnDoc xin giới thiệu tới các bạn bài Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn. Đây là tài liệu hay gồm các câu hỏi về đường tròn, giúp các bạn học sinh có thêm tài liệu ôn tập. Mời các bạn tải về tham khảo.

Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

CHỦ ĐỀ 1: SỰ XÁC ĐỊNH CỦA ĐƯỜNG TRÒN

Định nghĩa: Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách điểm Omột khoảng R kí hiệu là (O;R) hay (O)

+ Đường tròn đi qua các điểm A_{1},A_{2},...,A_{n}gọi là đường tròn ngoại tiếp đa giác A_{1}A_{2}...A_{n}

+ Đường tròn tiếp xúc với tất cả các cạnh của đa giác A_{1}A_{2}...A_{n} gọi là đường tròn nội tiếp đa giác đó.

Những tính chất đặc biệt cần nhớ:

+ Trong tam giác vuông trung điểm cạnh huyền là tâm vòng tròn ngoại tiếp

+ Trong tam giác đều, tâm vòng tròn ngoại tiếp là trọng tâm tam giác đó.

+ Trong tam giác thường:

Tâm vòng tròn ngoại tiếp là giao điểm của 3 đường trung trực của 3 cạnh tam giác đó

Tâm vòng tròn nội tiếp là giao điểm 3 đường phân giác trong của tam giác đó

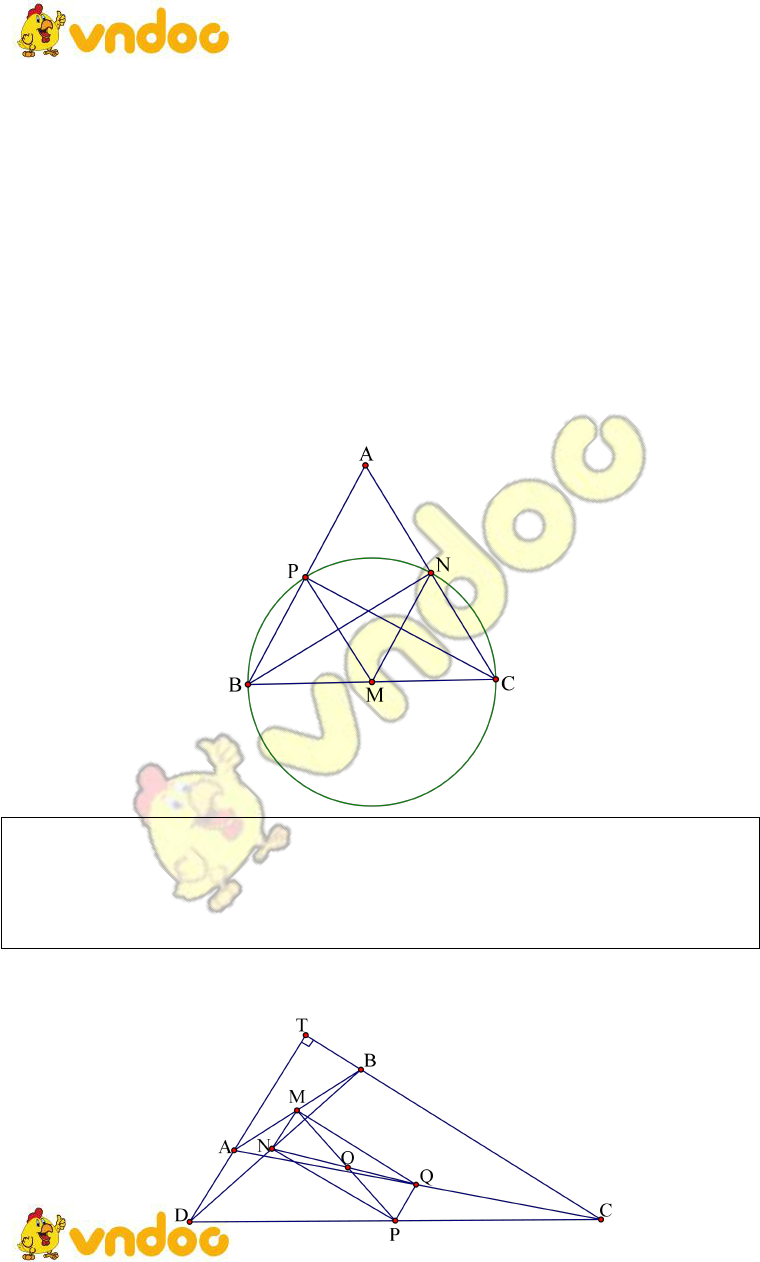
PHƯƠNG PHÁP: Để chứng minh các điểm A_{1},A_{2},...,A_{n} cùng thuộc một đường tròn ta chứng minh các điểm A_{1},A_{2},...,A_{n} cách đều điểm O cho trước.

CHỦ ĐỀ 2: VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN

1.Khi một đường thẳng có hai điểm chung A,B với đường tròn (O) ta nói đường thẳng cắt đường tròn tại hai điểm phân biệt. Khi đó ta có những kết quả quan trọng sau:

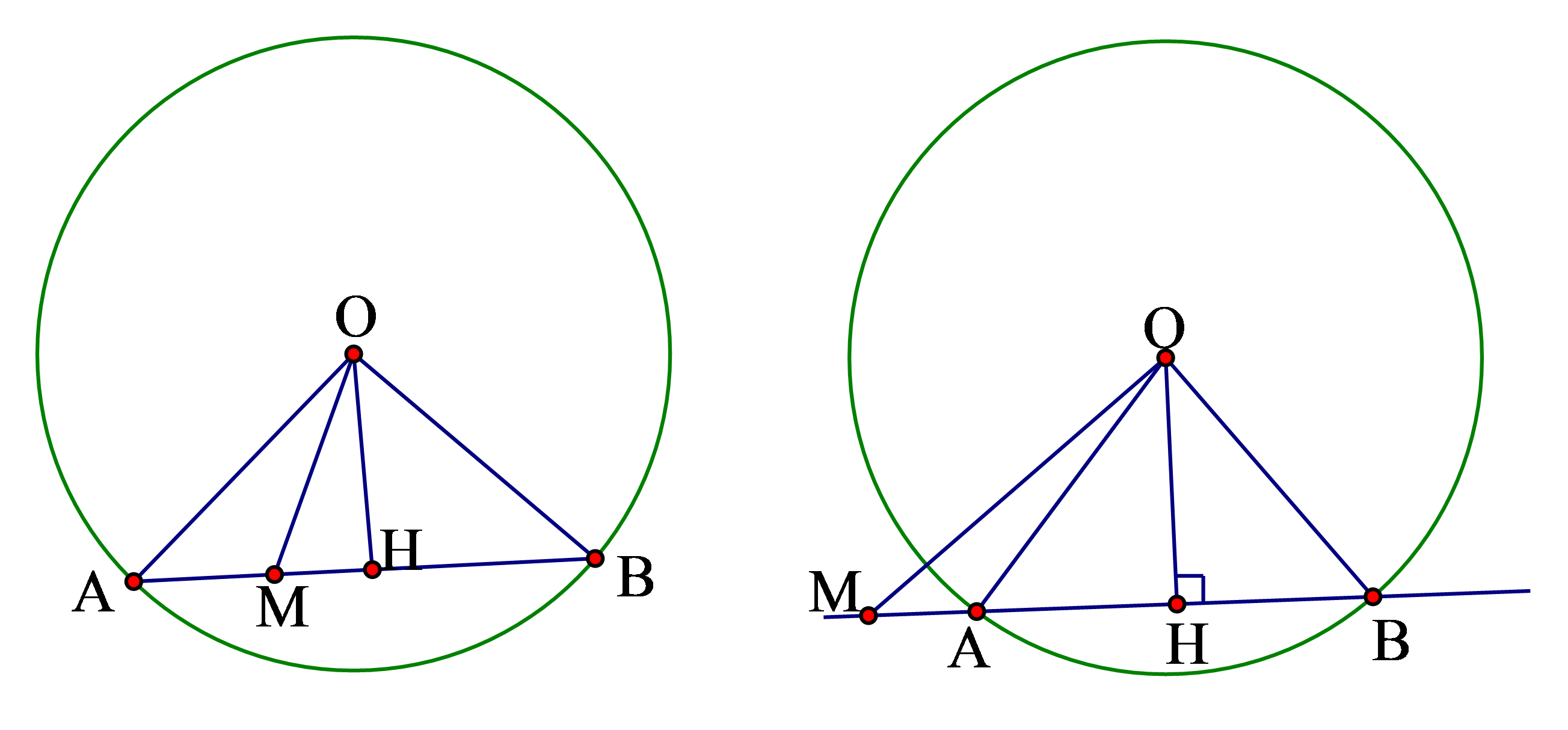
+ OH\bot AB \Rightarrow OH < R,HA = HB = \sqrt{R^{2} - OH^{2}}.

Theo định lý Pitago ta có: OH^{2} = MO^{2} - MH^{2}

Mặt khác ta cũng có: OH^{2} = R^{2} - AH^{2} nên suy

ra MO^{2} - MH^{2} = R^{2} - AH^{2} \Leftrightarrow MH^{2} - AH^{2} = MO^{2} - R^{2}

\Leftrightarrow (MH - AH)(MH + AH) = MO^{2} - R^{2}

+ Nếu M nằm ngoài đoạn AB thì MA.MB = MO^{2} - R^{2}

+ Nếu Mnằm trong đoạn AB thì MA.MB = R^{2} - MO^{2}

Mối liên hệ khoảng cách và dây cung: R^{2} = OH^{2} + \frac{AB^{2}}{4}

2. Khi một đường thẳng \Delta chỉ có một điểm chung Hvới đường tròn (O), ta nói đường thẳng tiếp xúc với đường tròn, hay \Delta là tiếp tuyến của đường tròn (O). Điểm H gọi là tiếp điểm của tiếp tuyến với đường tròn (O)

Như vậy nếu \Delta là tiếp tuyến của (O) thì \Delta vuông góc với bán kính đi qua tiếp điểm

Ta có OH = R

Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì

+ Điểm đó cách đều hai tiếp điểm

+ Tia kẻ từ điểm đó đến tâm O là tia phân giác góc tạo bởi 2 tiếp tuyến

+Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm

+ Tia kẻ từ tâm đi qua điểm đó thì vuông góc với đoạn thẳng nối hai tiếp điểm tại trung điểm của đoạn thẳng đó.

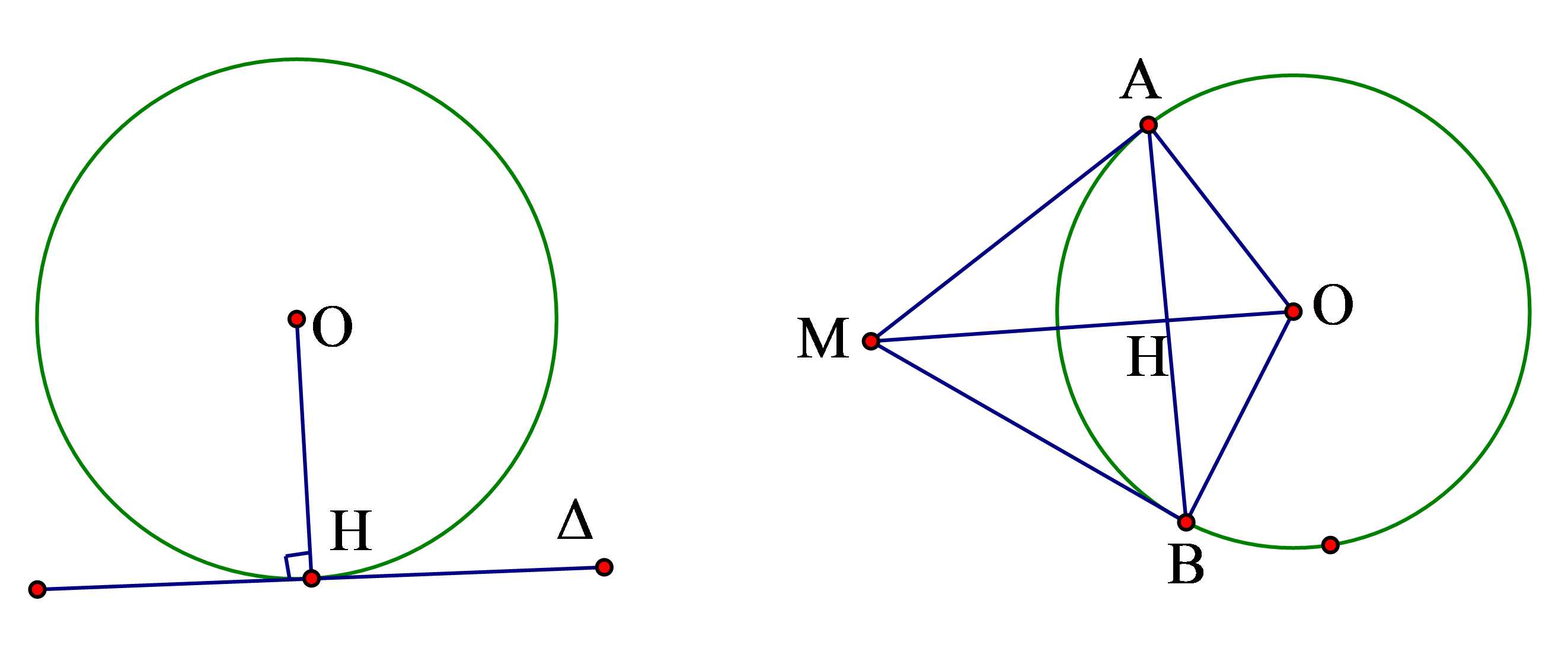
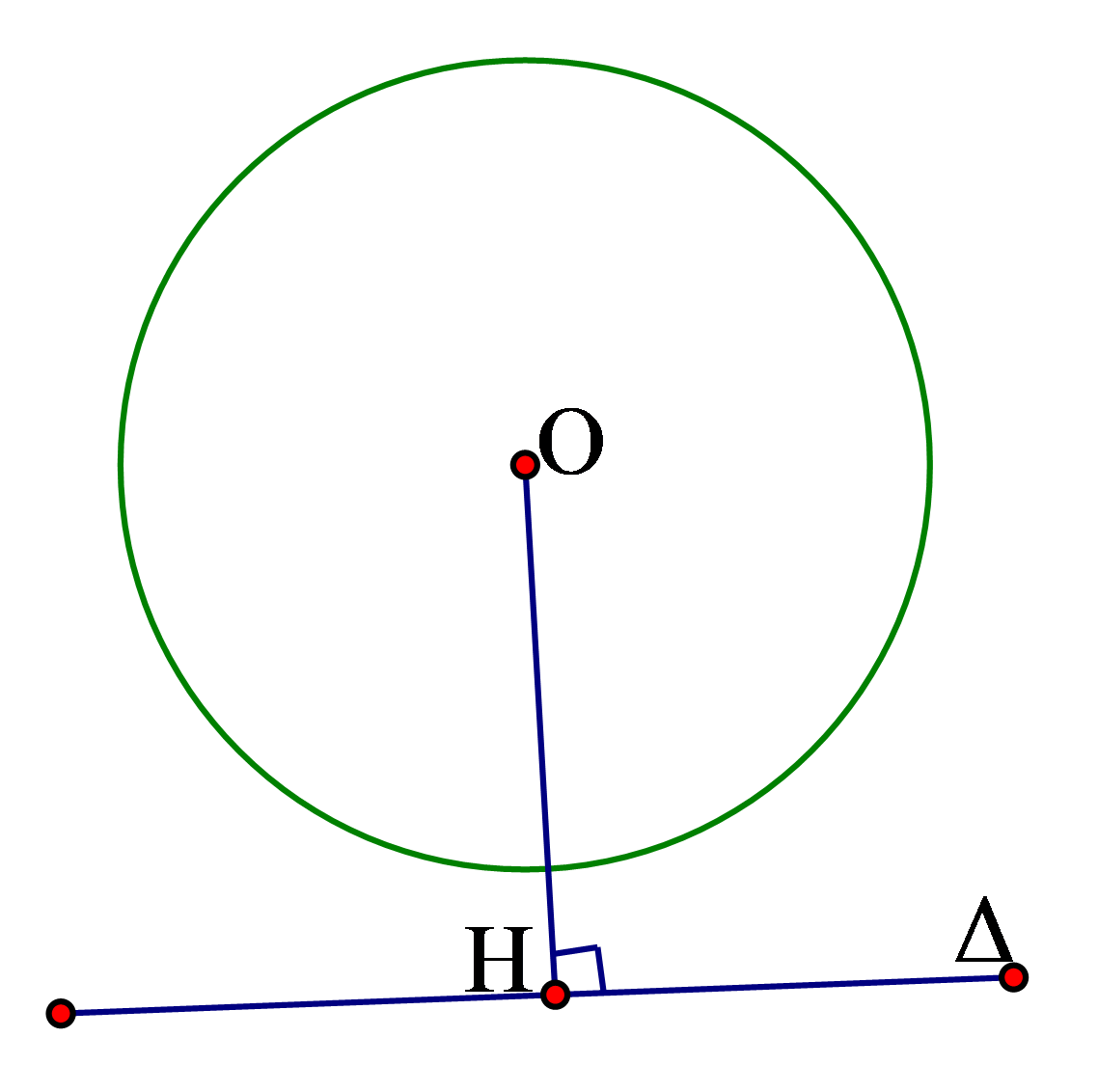
3. Khi một đường thẳng \Delta và đường tròn (O) không có điểm chung ta nói đường thẳng \Delta và đường tròn (O) không giao nhau. Khi đó OH > R

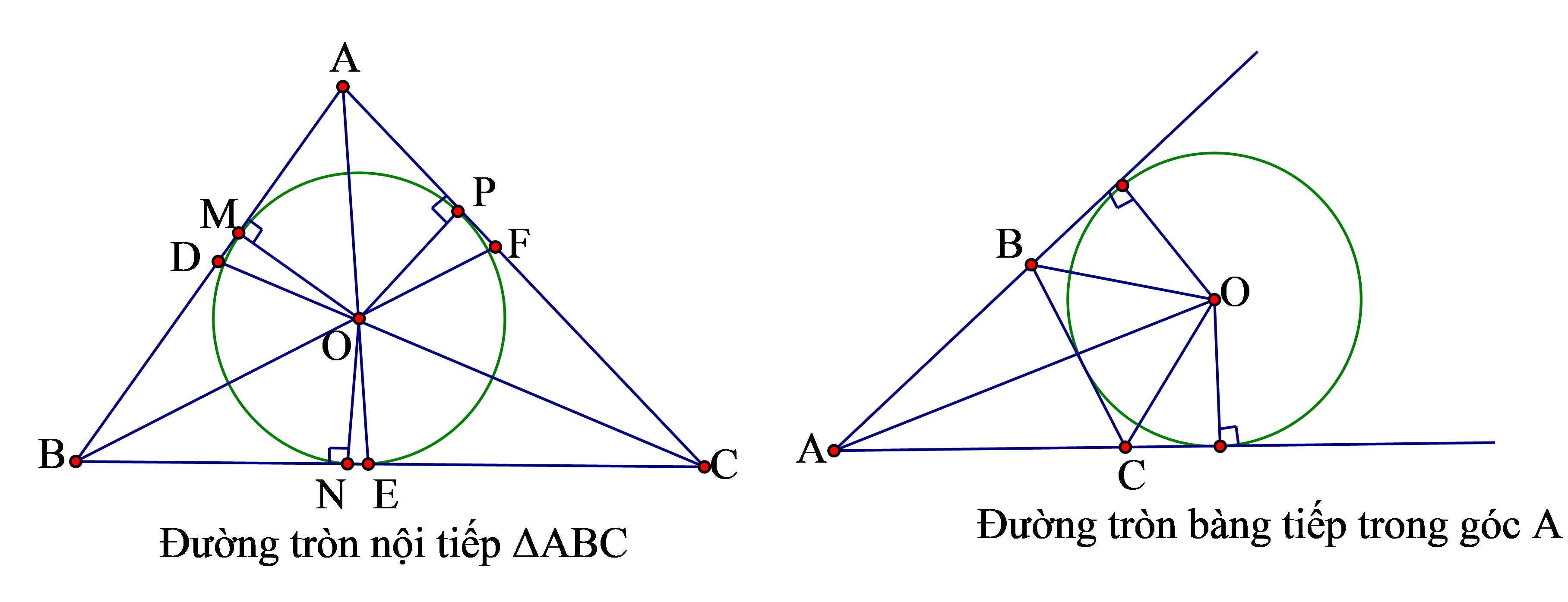
4. Đường tròn tiếp xúc với 3 cạnh tam giác là đường tròn nội tiếp tam giác

Đường tròn nội tiếp có tâm là giao điểm 3 đường phân giác trong của tam giác

5. Đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài hai cạnh kia gọi là đường tròn bàng tiếp tam giác

Tâm đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác ngoài góc B và góc C

Mỗi tam giác có 3 đường tròn bàng tiếp.

CHỦ ĐỀ 3. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN

Hai đường tròn cắt nhau

Hai đường tròn tiếp xúc nhau

Hai đường tròn không cắt nhau

Bài tập nâng cao: Bồi dưỡng HSG Toán 9: Bài tập nâng cao chuyên đề 2

Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn được VnDoc đã chia sẻ trên đây. Nội dung gồm lý thuyết và các câu hỏi bài tập trong chuyên đề đường tròn từ đó chuẩn bị tốt cho kì thi HSG lớp 9 sắp tới. Chúc các bạn học tốt, mời các bạn tham khảo

Ngoài Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 1 lớp 9, đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chọn file muốn tải về:

Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

3,2 MB

  • Tải file định dạng .DOC

    2,1 MB
1
1.865 Bài viết đã được lưu
Mục lục

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi

Tham khảo thêm

🖼️

Toán 9
Xem thêm
🖼️

Gợi ý cho bạn
Xem thêm

Thông tin thanh toán nhanh

Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

35.000đ

Hỗ trợ Zalo