6 Cách chứng minh tứ giác nội tiếp đường tròn
Chứng minh tứ giác nội tiếp đường tròn
Trong chương Hình học lớp 9, dạng toán chứng minh tứ giác nội tiếp đường tròn là kiến thức nền tảng nhưng lại khiến nhiều học sinh gặp khó khăn khi lựa chọn hướng chứng minh phù hợp. Mỗi bài toán có thể yêu cầu vận dụng linh hoạt các dấu hiệu khác nhau, nếu không nắm vững bản chất rất dễ rơi vào tình trạng lập luận dài dòng hoặc sai hướng.
Vì vậy, việc hệ thống hóa 6 cách chứng minh tứ giác nội tiếp đường tròn không chỉ giúp học sinh ghi nhớ nhanh mà còn nâng cao khả năng nhận diện dạng toán. Bài viết này sẽ trình bày đầy đủ các phương pháp chứng minh thường gặp, giúp người học áp dụng hiệu quả khi làm bài tập và ôn thi vào lớp 10.
6 Cách chứng minh tứ giác nội tiếp đường tròn
Chứng minh tứ giác nội tiếp trong một đường tròn là dạng bài tập có mặt thường xuyên trong các đề thi tuyển sinh môn toán vào lớp 10. Do đó mà học sinh không nên bỏ qua dạng này, hãy nghiên cứu thật kĩ càng phương pháp giải và luyện bài tập thật nhiều.
Hôm nay VnDoc.com xin gửi tới các bạn 6 cách chứng minh một tứ giác nội tiếp trong một đường tròn. Đây là những phương pháp chứng minh tứ giác nội tiếp khá cơ bản và thường xuyên sử dụng.
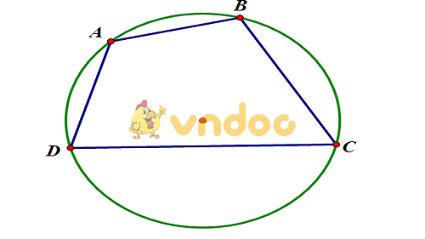
1. Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó.
Các bạn thấy rằng nếu cho trước một đường tròn tâm O, bán kính R thì bất kì điểm nào nằm trên đường tròn cũng cách đều tâm O một khoảng bằng R. Dựa vào đây để ta có một cách chứng minh tứ giác nội tiếp đường tròn.
Cụ thể: Cho một điểm I cố định và tứ giác ABCD. Nếu các bạn chứng minh được 4 điểm A, B, C, D cách đều điểm I, tức là IA=IB=IC=ID thì điểm I chính là tâm đường tròn đi qua 4 điểm A,B, C, D. Hay nói cách khác tứ giác ABCD nội tiếp đường tròn tâm I bán kính IA.
2. Chứng minh tứ giác có tổng 2 góc đối bằng 1800
Cụ thể: Cho tứ giác ABCD. Nếu các bạn chứng minh được 
hoặc thì tứ giác ABCD nội tiếp trong một đường tròn.
3. Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau.
Tức là: cho tứ giác ABCD, nếu các bạn chứng minh được rằng 
bằng nhau và cùng nhìn cạnh DC thì tứ giác ABCD nội tiếp đường tròn.
Đây chỉ là một ví dụ cho trường hợp này, các bạn có thể vẽ hình ra và dựa vào 1 ví dụ này để chỉ ra các trường hợp khác nhé.
4. Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn.
Cho tam giác ABCD. Nếu các bạn chứng minh được 
thì tức giác ABC cũng nội tiếp trong một đường tròn. Đây có thể nói là một trường hợp đặc biệt của trường hợp 2.
5. Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn.
Tức là nếu cho tam giác ABCD và các bạn chứng minh được góc ngoài tại đỉnh A mà bằng góc trong tại đỉnh C (tức là góc C của tứ giác đó) thì ABCD cũng nội tiếp đường tròn.
6. Chứng minh bằng phương pháp phản chứng
Chú ý: Các bạn có thể chứng minh tứ giác ABCD là một trong những hình đặc biệt sau: Tứ giác ABCD là hình thang cân, hình chữ nhật, hình vuông.
Bài viết tham khảo thêm:
- Tứ giác nội tiếp đường tròn lớp 9
- Chuyên đề Toán 9: Đường tròn ngoại tiếp tam giác Đường tròn nội tiếp tam giác
- Tổng hợp bài tập hình học ôn thi vào 10 có đáp án – Bộ đề t
- 29/12/2025 10:12
rọng tâm giải chi tiết - Chứng minh rằng biểu thức không đổi khi điểm M di chuyển trên đường tròn
- Chứng minh các điểm cùng thuộc một đường tròn
----------------------------------------------------
Việc nắm vững 6 cách chứng minh tứ giác nội tiếp đường tròn không chỉ giúp học sinh giải quyết hiệu quả các bài toán hình học lớp 9, mà còn tạo nền tảng quan trọng cho quá trình ôn thi vào lớp 10. Mỗi phương pháp chứng minh đều có ưu thế riêng, phù hợp với từng dạng bài và từng dữ kiện cho trước, vì vậy người học cần rèn luyện khả năng nhận dạng nhanh để lựa chọn cách làm tối ưu.
Thông qua việc vận dụng linh hoạt các dấu hiệu như tổng hai góc đối bằng 180°, góc ngoài bằng góc trong đối, hay bốn điểm cùng nhìn một đoạn thẳng dưới góc bằng nhau, học sinh sẽ hình thành tư duy hình học logic, tránh lối giải máy móc. Đây cũng là dạng toán thường xuyên xuất hiện trong đề thi học kỳ và đề tuyển sinh, đòi hỏi sự chắc chắn về kiến thức và kỹ năng trình bày.
Hy vọng bài viết đã giúp bạn hệ thống hóa đầy đủ các cách chứng minh tứ giác nội tiếp, từ đó nâng cao khả năng giải bài tập hình học đường tròn một cách chính xác và tự tin hơn. Đừng quên luyện tập thêm các bài toán vận dụng để thành thạo phương pháp và đạt kết quả cao trong các kỳ thi sắp tới.
