Chứng minh các hệ thức hình học

Trong Chuyên đề Toán lớp 9 luyện thi vào lớp 10, dạng bài chứng minh các hệ thức hình học đóng vai trò quan trọng trong việc rèn luyện tư duy logic, khả năng lập luận và kỹ năng vận dụng kiến thức hình học. Dạng toán này thường yêu cầu học sinh áp dụng các định lý quen thuộc như định lý Pythagore, hệ thức lượng trong tam giác vuông, các tính chất đường cao, đường trung tuyến, hoặc mối quan hệ giữa các yếu tố hình học để chứng minh một kết quả cho trước.

Việc nắm vững phương pháp và trình bày lời giải rõ ràng sẽ giúp học sinh ghi điểm tuyệt đối ở phần này. Bài viết sẽ hệ thống lại lý thuyết trọng tâm, phân tích phương pháp làm bài, kèm ví dụ minh họa chi tiết giúp bạn tự tin chinh phục mọi dạng đề liên quan.

I. Cách làm bài toán chứng minh các hệ thức hình học

+ Bài tập chứng minh các hệ thức hình học là bài toán mà ta phải chứng minh một đẳng thức đúng từ các dữ kiện để bài cho

+ Để làm được bài toán này ta có thể sử dụng định lú Ta-lét, tính chất đường phân giác, tam giác đồng dạng, các hệ thức lượng trong tam giác vuông

+ Các bước suy luận để chứng minh:

- Giả sử cần chứng minh: AB.AC = AD.AE

- Ta lập sơ đồ:

\(AB.AC = AD.AE \Leftarrow \frac{{AB}}{{AD}} = \frac{{AE}}{{AC}} \Leftarrow \Delta ABE\sim\Delta ADC\)

- Khi đó bước đầu tiên ta sẽ chứng minh tam giác đồng dạng để suy ra các cặp cạnh tương ứng tỉ lệ rồi chứng minh được hệ thức hình học đề bài đã ra

+ Ngoài ra có những bài toán ta sẽ không trực tiếp ra được hệ thức cần chứng minh mà cần phải chứng minh từng vế của hệ thức bằng với một hệ thức thứ ba

II. Bài tập ví dụ cho bài toán chứng minh các hệ thức hình học

Hướng dẫn giải

Hình vẽ minh họa

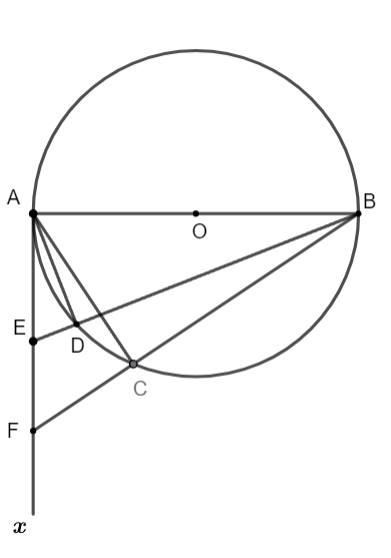
+ Có \(\widehat {ACB}\) nhìn đường kính AB nên \(\widehat {ACB} = {90^0}\)

+ Có Ax là tiếp tuyến, F thuộc Ax nên \(\widehat {FAB} = {90^0}\)

+ Xét tam giác FAB và tam giác ACB có:

\(\widehat B\) chung

\(\widehat {ACB} = \widehat {FAB}\left( { = {{90}^0}} \right)\)

Suy ra hai tam giác FAB và ACB đồng dạng theo trường hợp góc – góc

\(\Rightarrow \frac{{AB}}{{BC}} = \frac{{BF}}{{BA}} \Rightarrow BC.BF = A{B^2}\)(cặp cạnh tương ứng tỉ lệ) (1)

+ Có \(\widehat {ADB}\) nhìn đường kính AB nên \(\widehat {ADB} = {90^0}\)

+ Có Ax là tiếp tuyến, E thuộc Ax nên \(\widehat {EAB} = {90^0}\)

+ Xét tam giác EAB và tam giác ADB có:

\(\widehat B\) chung

\(\widehat {ADB} = \widehat {EAB}\left( { = {{90}^0}} \right)\)

Suy ra hai tam giác EAB và ADB đồng dạng theo trường hợp góc – góc

\(\Rightarrow \frac{{BE}}{{BA}} = \frac{{AB}}{{BD}} \Rightarrow BE.BD = A{B^2}\)(cặp cạnh tương ứng tỉ lệ) (2)

Từ (1) và (2) suy ra \(BC.BF = BE.BD\left( { = A{B^2}} \right)\) (đpcm)

Hướng dẫn giải

Hình vẽ minh họa

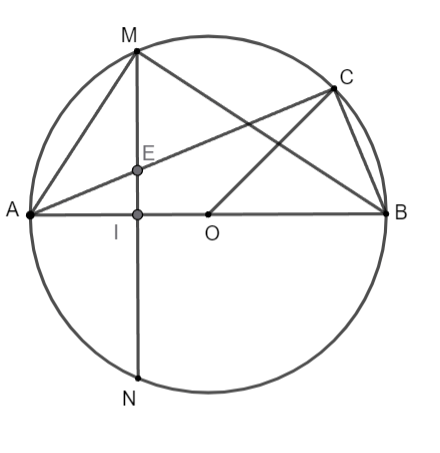
+ Có \(\widehat {AMB}\) nhìn đường kính AB nên \(\widehat {AMB} = {90^0}\)

+ Xét tam giác AMB có \(\widehat {AMB} = {90^0};MI \bot AB\)(MN vuông góc với AB tại I) có:

\(A{M^2} = AI.AB\)(hệ thức lượng trong tam giác vuông) (1)

+ Có \(\widehat {ACB}\) nhìn đường kính AB nên \(\widehat {ACB} = {90^0}\)

+ Xét tam giác AEI và tam giác ABC có:

\(\widehat {ACB} = \widehat {AIE}\left( { = {{90}^0}} \right)\)

\(\widehat {BAC}\)chung

Suy ra hai tam giác AEI và tam giác ABC đồng dạng với nhau theo trường hợp góc – góc

\(\Rightarrow \frac{{AE}}{{AB}} = \frac{{AI}}{{AC}} \Rightarrow AE.AC = AI.AB\)(cặp cạnh tương ứng tỉ lệ) (2)

Từ (1) và (2) suy ra \(A{M^2} = AE.AC\) (đpcm)

Hướng dẫn giải

Hình vẽ minh họa

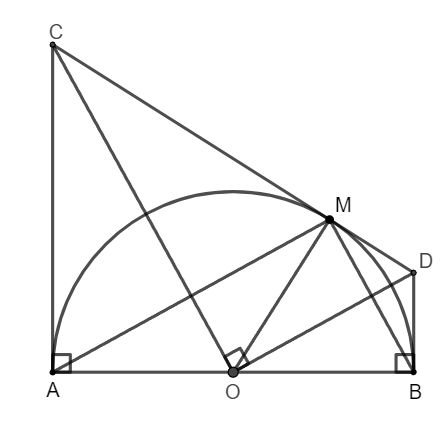
a) Vì tiếp tuyến tại A; M của đường tròn cắt nhau tại C nên \(\widehat{COA} = \widehat{COM}\)

Vì tiếp tuyến tại B; M của đường tròn cắt nhau tại D nên \(\widehat{DOB} = \widehat{DOM}\)

Ta có:

\(\widehat{AOB} = \widehat{AOC} + \widehat{COM} + \widehat{MOD} + \widehat{DOB} = 180^{0}\)

\(\Leftrightarrow 2\widehat{COM} + 2\widehat{MOD} = 180^{0} \Leftrightarrow \widehat{COM} + \widehat{MOD} = 90^{0}\)

Xét tam giác \(COD\) có \(\widehat{COM} + \widehat{MOD} = 90^{0}\)

Vậy tam giác COD vuông tại O.

Vì CD là tiếp tuyến của đường tròn (O) có tiếp điểm là M nên \(OM\bot CD\)

Vì tam giác COD vuông tại O có đường cao OM nên ta có: \(OM^{2} = MC.MD\)

b) Xét tam giác AOC vuông tại A có AO = R; PC = 2R

Áp dụng định lí Pythagore cho tam giác vuông AOC có:

\(OC^{2} = OA^{2} + AC^{2} \Leftrightarrow 4R^{2} = R^{2} + AC^{2}\)

\(\Leftrightarrow AC = R\sqrt{3}\)

Vì tiếp tuyến tại A; M của đường tròn (O) nên \(CA = CM = R\sqrt{3}\)

Xét tam giác vuông COD có OM là đường cao và \(OC^{2} = CM.CD\)

\(\Leftrightarrow 4R^{2} = R\sqrt{3}.CD\)

\(\Leftrightarrow CD = \frac{4R^{2}}{R\sqrt{3}}\)

\(\Rightarrow MD = CD - CM = \frac{4R\sqrt{3}}{3} - R\sqrt{3} = \frac{R\sqrt{3}}{3}\)

Vì tiếp tuyến tại B; M của đường tròn cắt nhau tại D nên \(DM = DB = \frac{R\sqrt{3}}{3}\).

Hướng dẫn giải

Hình vẽ minh họa

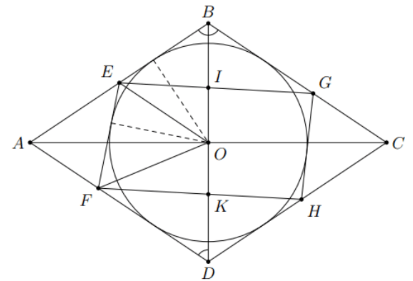
a) Tứ giác BEFD có:

\(\widehat{OBA} + \widehat{ODB} + \widehat{BEF} + \widehat{EFD} = 360^{0}\)

\(\Leftrightarrow 2\widehat{OBE} + 2\widehat{BEO} + 2\widehat{OFD} = 360^{0}\)

\(\Leftrightarrow \widehat{OBE} + \widehat{BEO} + \widehat{OFD} = 180^{0}\) mà \(\widehat{OBE} + \widehat{BEO} + \widehat{EOB} = 180^{0}\)

\(\Leftrightarrow \widehat{OFD} = \widehat{EOB}\)

\(\Rightarrow \Delta BOE\sim\Delta DFO(g - g) \Rightarrow \frac{BE}{OD} = \frac{OB}{DF}\)

\(\Rightarrow BE.DF = OB.OD(1)\)

b) Tương tự ta chứng minh được \(BG.DH = OB.OD(2)\)

Từ (1) và (2) suy ra \(BE.DF = BG.DH \Rightarrow \frac{BE}{DH} = \frac{BG}{DF}\)

\(\Rightarrow \Delta BEG\sim\Delta DHF(c - g - c)\)

\(\Rightarrow \widehat{BGE} = \widehat{DFH}\)

\(\Rightarrow \widehat{BGE} + \widehat{GBI} = \widehat{BGE} + \widehat{EBI} = \widehat{DFK} + \widehat{FDK}\)

\(\Rightarrow \widehat{OIG} = \widehat{OKF}\) (với I; K lần lượt là giao điểm của BD và EG; FH)

\(\Rightarrow EG//FH\).

Hướng dẫn giải

Hình vẽ minh họa

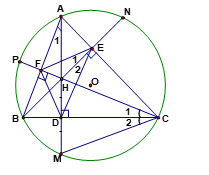
1. Xét tứ giác CEHD ta có:

∠ CEH = 90⁰ (Vì BE là đường cao)

∠ CDH = 90⁰ (Vì AD là đường cao)

=> ∠ CEH + ∠ CDH = 180⁰

Mà ∠ CEH và ∠ CDH là hai góc đối của tứ giác CEHD. Do đó CEHD làTha tứ giác nội tiếp

2. Theo giả thiết: BE là đường cao => BE ⊥ AC => ∠BEC = 90⁰.

CF là đường cao => CF ⊥ AB => ∠BFC = 90⁰.

Như vậy E và F cùng nhìn BC dưới một góc 90⁰ => E và F cùng nằm trên đường tròn đường kính BC.

Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.

3. Xét hai tam giác AEH và ADC ta có: ∠ AEH = ∠ ADC = 90⁰ ; ∠A là góc chung

=> ∆ AEH ∼ ∆ADC => \(\frac{AE}{AD}\ = \ \frac{AH}{AC}\) => AE.AC = AH.AD.

* Xét hai tam giác BEC và ADC ta có: ∠ BEC = ∠ ADC = 90⁰ ; ∠C là góc chung

=> ∆ BEC ∼ ∆ADC => \(\frac{BE}{AD}\ = \ \frac{BC}{AC}\) => AD.BC = BE.AC.

4. Ta có ∠C₁ = ∠A₁ (vì cùng phụ với góc ABC)

∠C₂ = ∠A₁ (vì là hai góc nội tiếp cùng chắn cung BM)

=> ∠C₁ = ∠ C₂ => CB là tia phân giác của góc HCM; lại có CB ⊥ HM => ∆ CHM cân tại C

=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.

5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn

=> ∠C₁ = ∠E₁ (vì là hai góc nội tiếp cùng chắn cung BF)

Cũng theo chứng minh trên CEHD là tứ giác nội tiếp

=> ∠C₁ = ∠E₂ (vì là hai góc nội tiếp cùng chắn cung HD)

=> ∠E₁ = ∠E₂ => EB là tia phân giác của góc FED.

Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

Hướng dẫn giải

Hình vẽ minh họa

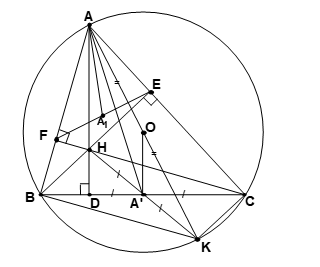
1. Tứ giác BFEC nội tiếp => ∠AEF = ∠ACB (cùng bù ∠BFE)

∠AEF = ∠ABC (cùng bù ∠CEF) => ∆ AEF ∼ ∆ ABC.

2. Vẽ đường kính AK => KB // CH ( cùng vuông góc AB); KC // BH (cùng vuông góc AC)

=> BHKC là hình bình hành => A’ là trung điểm của HK

=> OK là đường trung bình của ∆AHK => AH = 2OA’.

3. Áp dụng tính chất : nếu hai tam giác đồng dạng thì tỉ số giữa hia trung tuyến, tỉ số giữa hai bán kính các đường tròn ngoại tiếp bằng tỉ số đồng dạng. ta có :

∆ AEF ∼ ∆ ABC => \(\frac{R}{R'}\ = \ \frac{AA'}{AA_{1}}\) (1) trong đó R là bán kính đường tròn ngoại tiếp ∆ABC; R’ là bán kính đường tròn ngoại tiếp ∆ AEF; AA’ là trung tuyến của ∆ABC; AA₁ là trung tuyến của ∆AEF.

Tứ giác AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường tròn ngoại tiếp ∆AEF

Từ (1) => R.AA₁ = AA’. R’ = AA’ \(\frac{AH}{2}\) = AA’ . \(\frac{2A'O}{2}\)

Vậy R . AA₁ = AA’ . A’O (2)

4. Gọi B’, C’ lần lượt là trung điểm của AC, AB, ta có OB’⊥AC ; OC’⊥AB (bán kính đi qua trung điểm của một dây không qua tâm)

=> OA’, OB’, OC’ lần lượt là các đường cao của các tam giác OBC, OCA, OAB.

S_ABC = S_OBC+ S_OCA + S_OAB =\(\frac{1}{2}\)( OA’ . BC’ + OB’ . AC + OC’ . AB )

2S_ABC = OA’ . BC + OB’ . AC’ + OC’ . AB (3)

Theo (2) => OA’ = R . \(\frac{AA_{1}}{AA'}\) mà \(\frac{AA_{1}}{AA'}\)là tỉ số giữa 2 trung tuyến của hai tam giác đồng dạng AEF và ABC nên \(\frac{AA_{1}}{AA'}\) = \(\frac{EF}{BC}\).

Tương tự ta có : OB’ = R .\(\frac{FD}{AC}\); OC’ = R . \(\frac{ED}{AB}\) Thay vào (3) ta được

2S_ABC = R (\(\frac{EF}{BC}.BC + \frac{FD}{AC}.AC + \frac{ED}{AB}.AB\)) ⬄ 2S_ABC = R(EF + FD + DE)

* R(EF + FD + DE) = 2S_ABC mà R không đổi nên (EF + FD + DE) đạt gí trị lớn nhất khi S_ABC.

Ta có S_ABC = \(\frac{1}{2}\)AD.BC do BC không đổi nên S_ABC lớn nhất khi AD lớn nhất, mà AD lớn nhất khi A là điểm chính giỡa của cung lớn BC

III. Bài tập tự luyện về bài toán chứng minh các hệ thức hình học

Bài 1: Cho đường tròn O cà dây CD. A là điểm chính giữa cung CD. M thuộc CD, dây AN qua M

a, Chứng minh \(A{C^2} = AM.AN\).

b, Chứng minh \(AD.DN = DM.AN\).

Bài 2: Cho tam giác đều ABC nội tiếp (O). D là điểm trên cung nhỏ BC. CD và AB kéo dài cắt nhau ở M, BD và AC kéo dài cắt nhau ở N. Chứng minh \(A{B^2} = BM.CN\).

Bài 3: Cho đường tròn (O) có đường kính AB =. Qua A kẻ tiếp tuyến xy. Một điểm M thuộc Ax, nối BM cắt (O) tại C. Chứng minh \(M{A^2} = MB.MC\).

Bài 4: Tam giác AMB cân tại M nội tiếp trong đường tròn (O; R). Kẻ MH vuông góc với AB (H thuộc AB), MH cắt đường tròn tại N. Trên tia đối BA lấy điểm C. MC cắt đường tròn tại D. ND cắt AB tại E. Chứng minh tứ giác MDEH nội tiếp và chứng minh các hệ thức sau: \(N{B^2} = NE.ND\) và \(AC.BE = BC.AE\).

Bài 5: Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại hai điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD. Kẻ AH vuông góc với MO tại H. Chứng minh \(OH.OM = {R^2}\).

-------------------------------------------------------------------

Dạng bài chứng minh các hệ thức hình học không chỉ kiểm tra khả năng ghi nhớ định lý mà còn đánh giá mức độ linh hoạt trong vận dụng kiến thức của học sinh. Khi luyện tập thường xuyên, bạn sẽ:

• Thành thạo việc sử dụng các định lý, hệ thức lượng và tính chất hình học.

• Biết cách phân tích đề, vẽ hình minh họa chính xác và lựa chọn phương pháp chứng minh tối ưu.

• Nâng cao kỹ năng lập luận chặt chẽ, trình bày mạch lạc và khoa học.

• Tự tin xử lý những bài toán tổng hợp đòi hỏi kết hợp nhiều yếu tố hình học khác nhau.

Để đạt kết quả cao, bạn nên luyện giải cả các bài tập cơ bản và nâng cao, đồng thời chú trọng vào cách trình bày để vừa đảm bảo tính logic vừa rõ ràng, dễ hiểu. Việc thành thạo chứng minh các hệ thức hình học sẽ giúp bạn không chỉ vững vàng trong kỳ thi vào lớp 10 mà còn tạo nền tảng chắc chắn cho các bậc học cao hơn. Đây chính là chìa khóa để bạn bứt phá điểm số và làm chủ phần hình học trong mọi kỳ thi quan trọng.