VnDoc.com

Bài tập Vị trí tương đối của đường thẳng và đường tròn lớp 9

Chuyên đề Toán 9 ôn thi vào 10 (nâng cao)

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Vị trí tương đối của đường thẳng và đường tròn (nâng cao) - Có đáp án

Vị trí tương đối của đường thẳng và đường tròn là một trong những chuyên đề quan trọng của chương trình Toán 9, thường xuyên xuất hiện trong các đề thi vào lớp 10. Dạng toán này không chỉ giúp học sinh rèn luyện kỹ năng hình học mà còn phát triển tư duy phân tích, lập luận logic. Tài liệu dưới đây cung cấp hệ thống bài tập nâng cao có lời giải chi tiết, giúp học sinh ôn luyện toàn diện, làm quen với nhiều dạng câu hỏi và nâng cao khả năng xử lý các tình huống phức tạp trong đề thi.

A. Vị trí tương đối của đường thẳng và đường tròn

1.Khi một đường thẳng có hai điểm chung $A,B$ với đường tròn $(O)$ ta nói đường thẳng cắt đường tròn tại hai điểm phân biệt. Khi đó ta có những kết quả quan trọng sau:

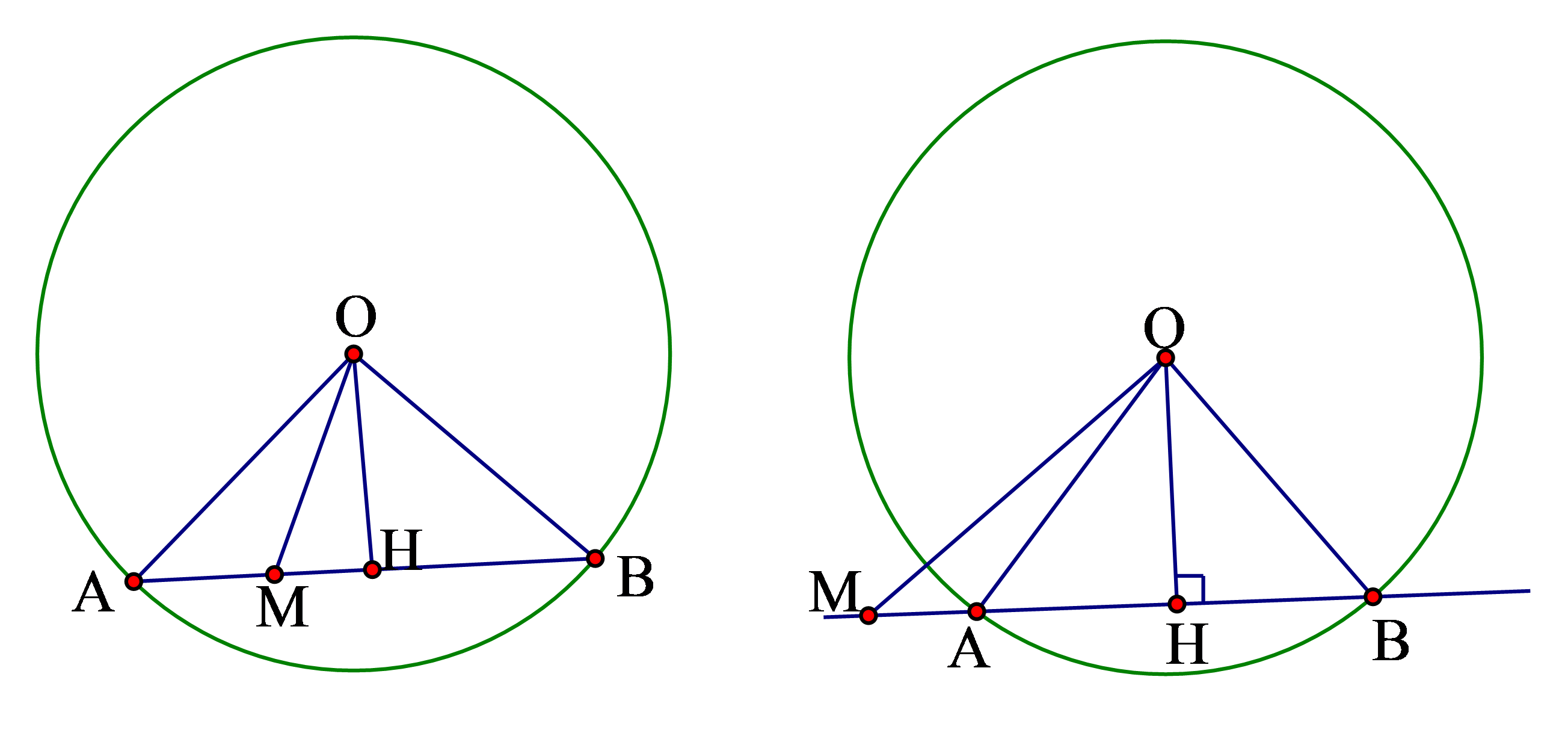
+ $OH\bot AB \Rightarrow OH < R,HA = HB = \sqrt{R^{2} - OH^{2}}$ $OH\bot AB \Rightarrow OH < R,HA = HB = \sqrt{R^{2} - OH^{2}}$. Theo định lý Pithagore ta có: $OH^{2} = MO^{2} - MH^{2}$ $OH^{2} = MO^{2} - MH^{2}$

Mặt khác ta cũng có: $OH^{2} = R^{2} - AH^{2}$ $OH^{2} = R^{2} - AH^{2}$ nên suy ra

$MO^{2} - MH^{2} = R^{2} - AH^{2} \Leftrightarrow MH^{2} - AH^{2} = MO^{2} - R^{2}$ $MO^{2} - MH^{2} = R^{2} - AH^{2} \Leftrightarrow MH^{2} - AH^{2} = MO^{2} - R^{2}$ $\Leftrightarrow (MH - AH)(MH + AH) = MO^{2} - R^{2}$ $\Leftrightarrow (MH - AH)(MH + AH) = MO^{2} - R^{2}$

+ Nếu $M$ nằm ngoài đoạn $AB$ thì $MA.MB = MO^{2} - R^{2}$ $MA.MB = MO^{2} - R^{2}$

+ Nếu $M$ nằm trong đoạn $AB$ thì $MA.MB = R^{2} - MO^{2}$ $MA.MB = R^{2} - MO^{2}$ Mối liên hệ khoảng cách và dây cung: $R^{2} = OH^{2} + \frac{AB^{2}}{4}$ $R^{2} = OH^{2} + \frac{AB^{2}}{4}$

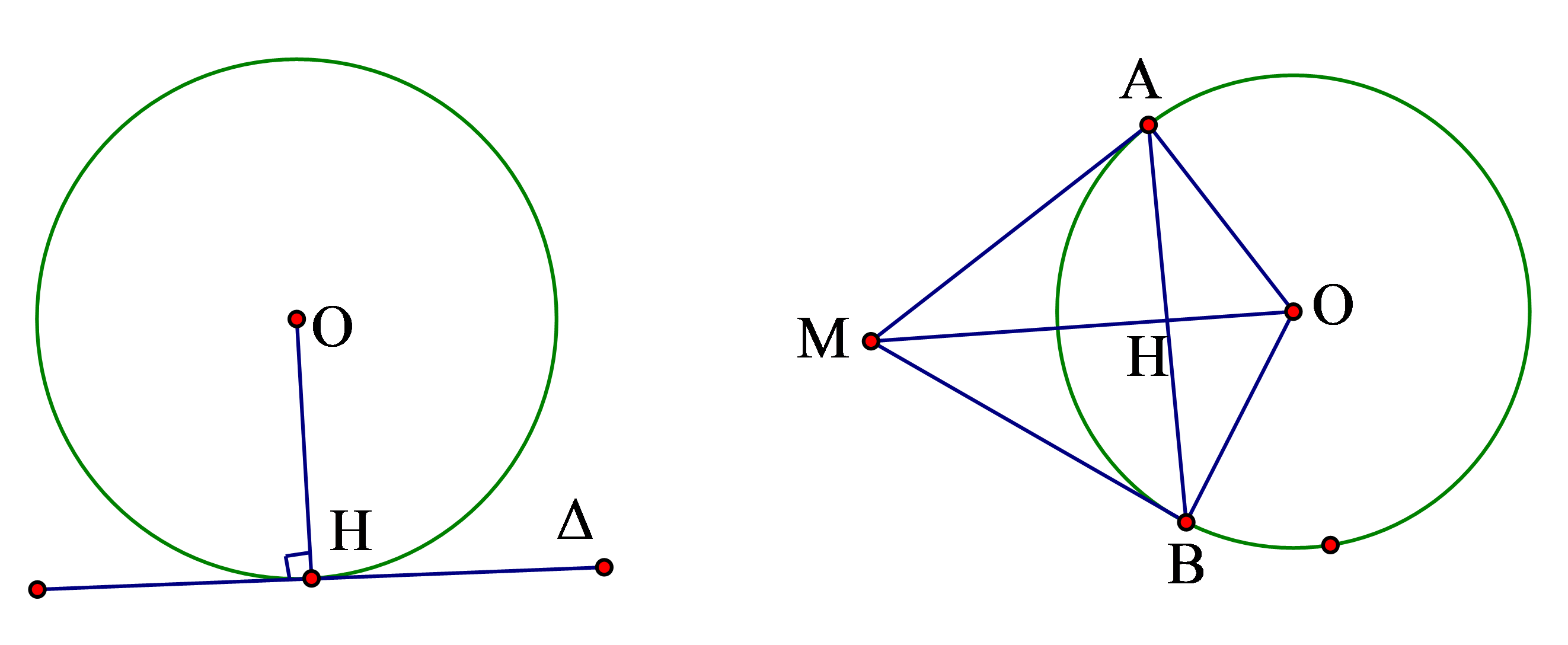
2. Khi một đường thẳng $\Delta$ $\Delta$ chỉ có một điểm chung $H$ với đường tròn $(O)$, ta nói đường thẳng tiếp xúc với đường tròn, hay $\Delta$ $\Delta$ là tiếp tuyến của đường tròn $(O)$. Điểm $H$ gọi là tiếp điểm của tiếp tuyến với đường tròn $(O)$

Như vậy nếu $\Delta$ $\Delta$ là tiếp tuyến của $(O)$ thì $\Delta$ $\Delta$ vuông góc với bán kính đi qua tiếp điểm.

Ta có $OH = R$

Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:

+ Điểm đó cách đều hai tiếp điểm

+ Tia kẻ từ điểm đó đến tâm $O$ là tia phân giác góc tạo bởi 2 tiếp tuyến

+Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm

+ Tia kẻ từ tâm đi qua điểm đó thì vuông góc với đoạn thẳng nối hai tiếp điểm tại trung điểm của đoạn thẳng đó.

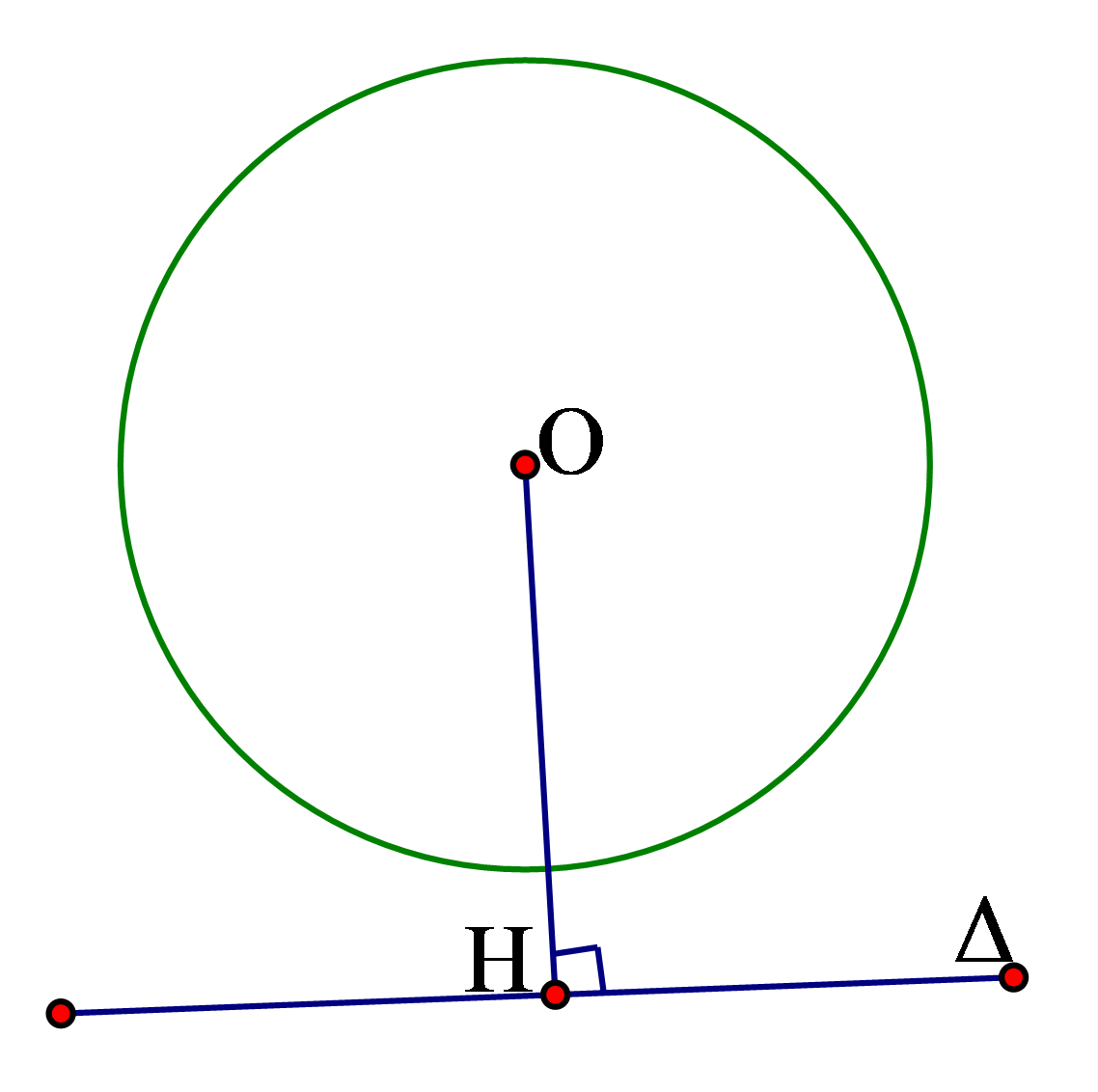
3. Khi một đường thẳng $\Delta$ $\Delta$ và đường tròn $(O)$ không có điểm chung ta nói đường thẳng $\Delta$ $\Delta$ và đường tròn $(O)$ không giao nhau. Khi đó $OH > R$

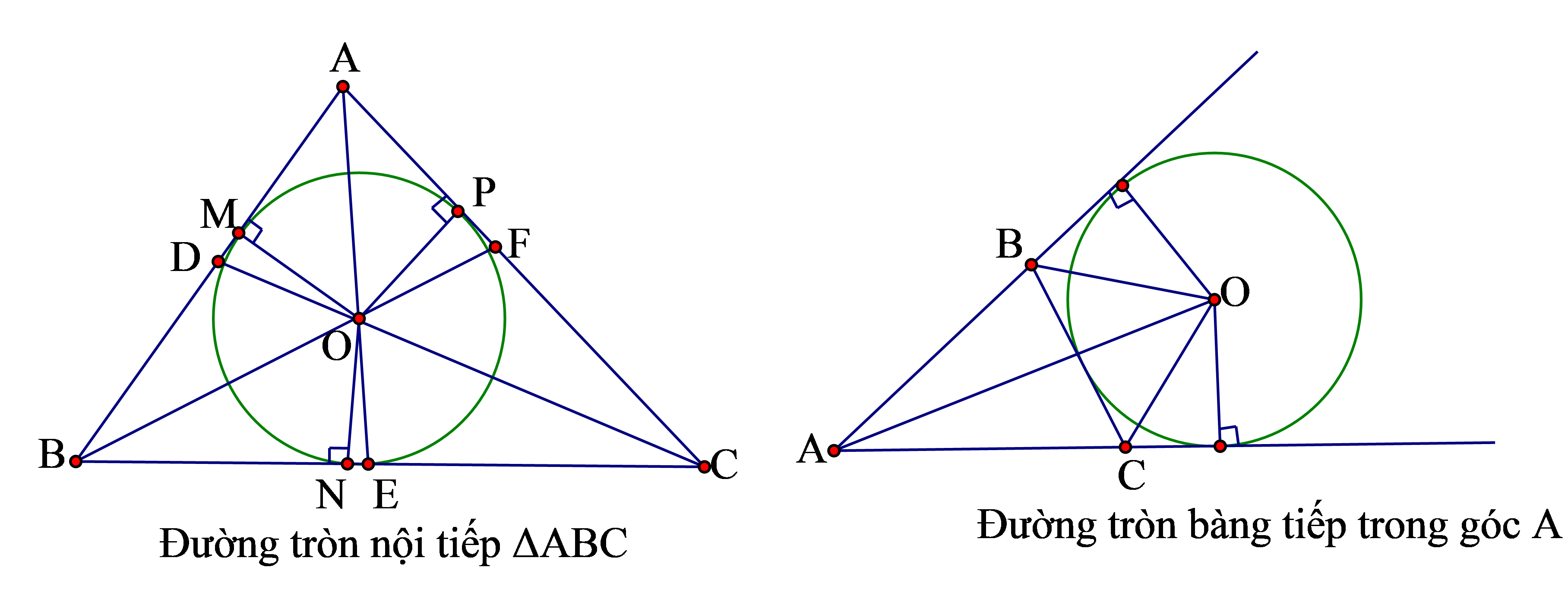
4. Đường tròn tiếp xúc với 3 cạnh tam giác là đường tròn nội tiếp tam giác

Đường tròn nội tiếp có tâm là giao điểm 3 đường phân giác trong của tam giác

5. Đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài hai cạnh kia gọi là đường tròn bàng tiếp tam giác

Tâm đường tròn bàng tiếp tam giác trong góc $A$ là giao điểm của hai đường phân giác ngoài góc $B$ và góc $C$.

Mỗi tam giác có 3 đường tròn bàng tiếp.

B. Bài tập vị trí tương đối của đường thẳng và đường tròn có hướng dẫn chi tiết

Ví dụ 1. Cho hình thang vuông $ABCD$ $(\widehat{A} = \widehat{B} = 90^{0})$ $(\widehat{A} = \widehat{B} = 90^{0})$ có $O$ là trung điểm của $AB$ và góc $\widehat{COD} = 90^{0}$ $\widehat{COD} = 90^{0}$. Chứng minh $CD$ là tiếp tuyến của đường tròn đường kính $AB$.

Giải:

Hình vẽ minh họa:

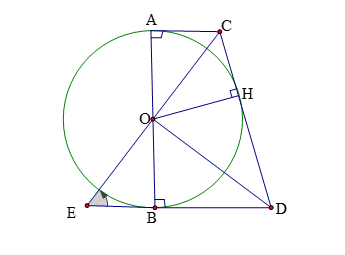
Kéo dài $OC$ cắt $BD$ tại $E$ vì $\widehat{COD} = 90^{0}$ $\widehat{COD} = 90^{0}$ suy ra $\widehat{EOD} = 90^{0}$ $\widehat{EOD} = 90^{0}$.

Xét tam giác $COD$ và $\Delta EOD$ $\Delta EOD$ ta có $OD$ chung

$\frac{OC}{OD} = \frac{OA}{OB} = 1 \Rightarrow OC = OD \Rightarrow \Delta COD = \Delta\Delta EOD$ $\frac{OC}{OD} = \frac{OA}{OB} = 1 \Rightarrow OC = OD \Rightarrow \Delta COD = \Delta\Delta EOD$.

Suy ra $DC = DE$ hay tam giác $ECD$ cân tại $D$.

Kẻ $OH\bot CD$ $OH\bot CD$ thì $\Delta OBD = \Delta OHD \Rightarrow OH = OB$ $\Delta OBD = \Delta OHD \Rightarrow OH = OB$ mà $OB = OA \Rightarrow OH = OB = OA$ $OB = OA \Rightarrow OH = OB = OA$ hay $A,H,B$ thuộc đường tròn $(O)$.

Do đó $CD$ là tiếp tuyến của đường tròn đường kính $AB$.

Ví dụ 2. Cho hình vuông $ABCD$ có cạnh bằng $a$. Gọi $M,N$ là hai điểm trên các cạnh $AB,AD$ sao cho chu vi tam giác $AMN$ bằng $2a$. Chứng minh đường thẳng $MN$ luôn tiếp xúc với $1$ đường tròn cố định.

Giải:

Hình vẽ minh họa

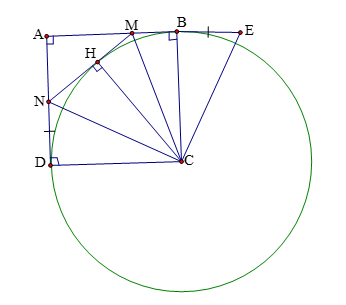
Trên tia đối của $BA$ ta lấy điểm $E$ sao cho $BE = ND$.

Ta có $\Delta BCE = \Delta DCN \Rightarrow CN = CE$ $\Delta BCE = \Delta DCN \Rightarrow CN = CE$.

Theo giả thiết ta có:

$MN + AM + AN = AB + AD =$ $AM + MB + AN + DN = AM + AN + MB + BE$.

uy ra $MN = MB + BE = ME$.

Từ đó ta suy ra $\Delta MNC = \Delta MEC \Rightarrow \widehat{CMN} = \widehat{CMB}$ $\Delta MNC = \Delta MEC \Rightarrow \widehat{CMN} = \widehat{CMB}$.

Kẻ $CH\bot MN \Rightarrow$ $CH\bot MN \Rightarrow$ $CH = CB = CD = a$.

Vậy $D,H,B$ thuộc đường tròn tâm $C$ bán kính $CB = a$ suy ra $MN$ luôn tiếp xúc với đường tròn tâm $C$ bán kính bằng $a$.

Ví dụ 3. Cho tam giác $ABC$ cân tại $A$ đường cao $BH$. Trên nửa mặt phẳng chứa $C$ bờ $AB$ vẽ $Bx\bot BA$ $Bx\bot BA$ cắt đường tròn tâm $B$ bán kính $BH$ tại $D$. Chứng minh $CD$ là tiếp tuyến của $(B)$.

Giải:

Hình vẽ minh họa

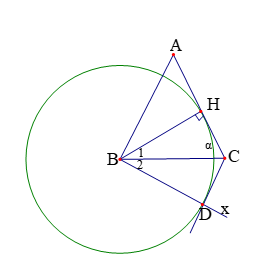
Vì tam giác $ABC$ cân tại $A$ nên ta có: $\widehat{B} = \widehat{C} = \alpha$ $\widehat{B} = \widehat{C} = \alpha$.

Vì $Bx\bot BA \Rightarrow \widehat{B_{2}} + \alpha = 90^{0}$ $Bx\bot BA \Rightarrow \widehat{B_{2}} + \alpha = 90^{0}$.

Mặt khác ta cũng có $\widehat{B_{1}} + \alpha = 90^{0} \Rightarrow \widehat{B_{1}} = \widehat{B_{2}}$ $\widehat{B_{1}} + \alpha = 90^{0} \Rightarrow \widehat{B_{1}} = \widehat{B_{2}}$.

Hai tam giác $BHC$ và $\Delta BDC$ $\Delta BDC$ có $BC$ chung, $\widehat{B_{1}} = \widehat{B_{2}}$ $\widehat{B_{1}} = \widehat{B_{2}}$, $BH = BD = R$

Suy ra $\Delta BHC = \Delta BDC(c.g.c)$ $\Delta BHC = \Delta BDC(c.g.c)$ suy ra $\widehat{BHC} = \Delta\widehat{BDC} = 90^{0}$ $\widehat{BHC} = \Delta\widehat{BDC} = 90^{0}$.

Nói cách khác $CD$ là tiếp tuyến của đường tròn $(B)$.

C. Bài tập tự rèn luyện có đáp án

Bài tập 1. Cho tam giác $ABC$ vuông tại $A$ $(AB < AC)$ đường cao $AH$. Gọi $E$ là điểm đối xứng với $B$ qua $H$. Đường tròn tâm $O$ đường kính $EC$cắt $AC$ tại $K$. Chứng minh $HK$ là tiếp tuyến của đường tròn $(O)$.

Bài tập 2. Cho tam giác $ABC$vuông tại $A$đường cao $AH$. Vẽ đường tròn tâm $A$ bán kính $AH$ kẻ các tiếp tuyến $BD,CE$ với $(A)$ ($D,E$ là các tiếp điểm khác $H$). Chứng minh $DE$ tiếp xúc với đường tròn đường kính $BC$.

Bài tập 3. Cho tam giác $ABC$ ngoại tiếp đường tròn tâm $I$ bán kính $r$. Giả sử $(I;r)$ tiếp xúc với các cạnh $AB,BC,CE$ lần lượt tại $D,E,F$. Đặt $AB = c,BC = a,AC = b,AD = x,BE = y,CF = z$.

a. Hãy tính $x,y,z$ theo $a,b,c$

b. Chứng minh $S = p.r$ (trong đó $S$ là diện tích tam giác $p$ là nữa chu vi tam giác, r là bán kính vòng tròn ngoại tiếp tam giác.

c. Chứng minh: $\frac{1}{r} = \frac{1}{h_{a}} + \frac{1}{h_{b}} + \frac{1}{h_{c}}$ $\frac{1}{r} = \frac{1}{h_{a}} + \frac{1}{h_{b}} + \frac{1}{h_{c}}$ trong đó $(h_{a};h_{b};h_{c})$ $(h_{a};h_{b};h_{c})$ lần lượt là đường cao kẻ từ các đỉnh $A,B,C$ của tam giác $A,B,C$.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

------------------------------------------------------------

Chinh phục dạng toán vị trí tương đối giữa đường thẳng và đường tròn sẽ giúp học sinh tự tin hơn trong phần hình học của đề thi vào lớp 10. Hy vọng tài liệu này sẽ là nguồn ôn luyện hữu ích, hỗ trợ bạn rèn luyện tư duy và đạt kết quả cao trong kỳ thi sắp tới. Đừng quên luyện tập thường xuyên và ghi nhớ các phương pháp giải hiệu quả!

Tải về

Chọn file muốn tải về: