VnDoc.com

Chuyên đề Vị trí tương đối của hai đường tròn – Có đáp án

Ôn thi vào lớp 10 môn Toán

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề Toán 9: Vị trí tương đối của hai đường tròn (nâng cao) - Có đáp án

Vị trí tương đối của hai đường tròn là một chuyên đề quan trọng trong chương trình Toán 9, thường xuất hiện trong các đề thi vào lớp 10 với nhiều dạng bài đa dạng từ cơ bản đến nâng cao. Việc nắm vững lý thuyết và luyện tập các bài tập chọn lọc giúp học sinh nâng cao khả năng tư duy hình học, phân tích mối quan hệ giữa các yếu tố hình học trong mặt phẳng. Tài liệu này tổng hợp các dạng bài điển hình về vị trí tương đối của hai đường tròn có đáp án và lời giải chi tiết, giúp học sinh ôn tập hiệu quả và sẵn sàng chinh phục kỳ thi vào 10.

A. Hai đường tròn tiếp xúc nhau

Xét hai đường tròn $(O;R),(O';R')$

Khi hai đường tròn tiếp xúc nhau, thì có thể xảy ra 2 khả năng.

Xét trường hợp: Hai đường tròn tiếp xúc ngoài:

+ Điều kiện $R + R' = OO'$. Tiếp điểm nằm trên đường nối tâm của hai đường tròn. Đường nối tâm là trục đối xứng của hai đường tròn.

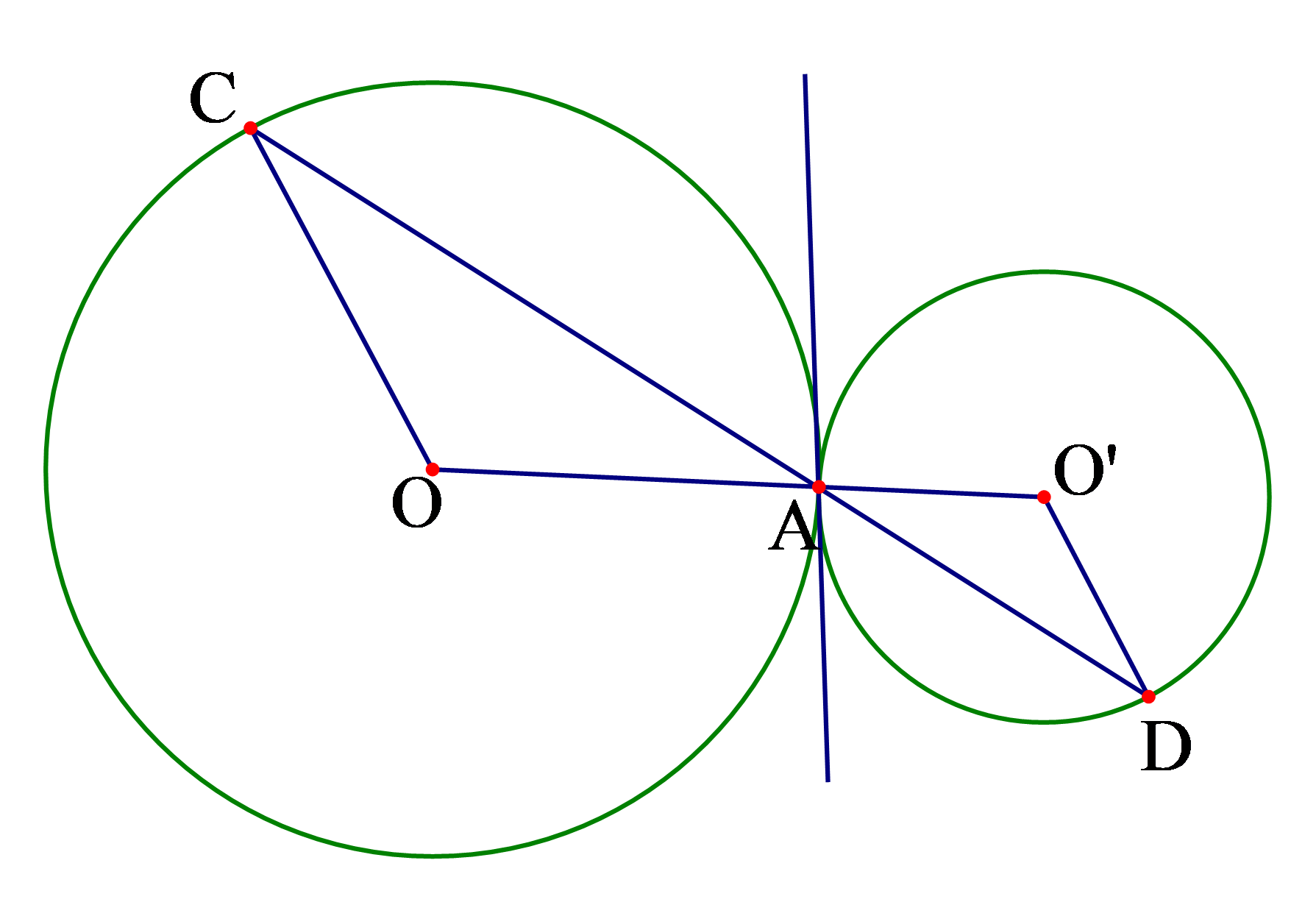
Ví dụ: Cho hai đường tròn $(O)$ và $(O')$ tiếp xúc ngoài tại $A$. Qua $A$ kẻ một cát tuyến cắt $(O)$ tại $C$, cắt đường tròn $(O')$ tại $D$.

a. Chứng minh $OC//O'D$

b. Kẻ tiếp tuyến chung ngoài $MN$, gọi $P$, $Q$ lần lượt là các điểm đối xứng với $M,N$ qua $OO'$. Chứng minh $MNQP$ là hình thang cân và $MN + PQ = MP + NQ$

c. Tính góc $\widehat{MAN}$ $\widehat{MAN}$ . Gọi $K$ là giao điểm của $AM$ với $(O')$. Chứng minh $N,O',K$ thẳng hàng.

Giải:

Hình vẽ minh họa

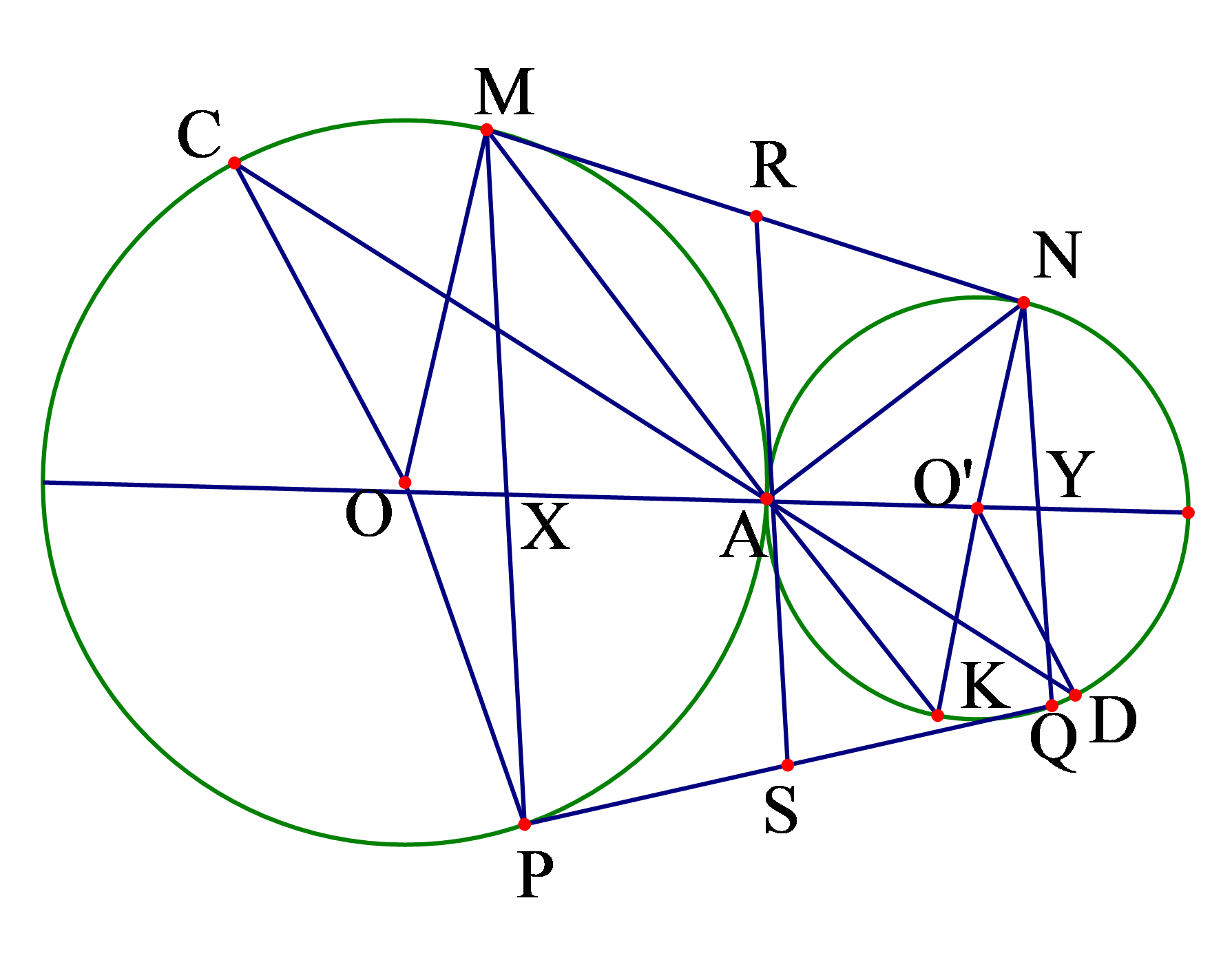
a) Do hai đường tròn $(O)$ và $(O')$ tiếp xúc ngoài tại $A$nên $A$ nằm trên $OO'$.Ta có $\widehat{CAO} = \widehat{DAO}$ $\widehat{CAO} = \widehat{DAO}'$.

Lại có $\widehat{OCA} = \widehat{OAD},\widehat{O$ $\widehat{OCA} = \widehat{OAD},\widehat{O'AD} = \widehat{O'DA}$ vì các tam giác $\Delta COA,\Delta DO$ $\Delta COA,\Delta DO'A$ là tam giác cân.

Từ đó suy ra $\widehat{OCA} = \widehat{O$ $\widehat{OCA} = \widehat{O'DA} \Leftrightarrow OC//O'D$

b) + Vì $MP\bot OO$ $MP\bot OO',NQ\bot OO' \Rightarrow MP//OO' \Rightarrow MNQP$ là hình thang.

Vì $M$ đối xứng với $P$ qua $OO'$, $N$ đối xứng với $Q$ qua $OO'$ và $O$ luôn đối xứng với $O$ qua $OO'$ nên $\widehat{OPM} = \widehat{OMP} = 90^{0}$ $\widehat{OPM} = \widehat{OMP} = 90^{0}$.

Mặt khác $\widehat{MPQ},\widehat{PMN}$ $\widehat{MPQ},\widehat{PMN}$ cùng phụ với các góc $\widehat{OPM} = \widehat{OMP}$ $\widehat{OPM} = \widehat{OMP}$ nên $\widehat{MPQ} = \widehat{PMN}$ $\widehat{MPQ} = \widehat{PMN}$ suy ra $MNQP$ là hình thang cân.

(Chú ý: Từ đây ta cũng suy ra $PQ$ là tiếp tuyến chung của hai đường tròn)

+ Kẻ tiếp tuyến chung qua $A$ của hai đường tròn cắt $MN,PQ$ tại $R,S$ thì ta có: $RM = RA = RN,SA = SP = SQ$ suy ra $MN + PQ = 2RS$. Mặt khác $RS$ cũng là đường trung bình của hình thang nên $MP + NQ = 2RS$ hay $MP + NQ = MN + PQ$

c). Từ câu $b$ ta có $AR = RM = RN$ nên tam giác $MAN$ vuông tại $A$, từ đó suy ra $\widehat{NAK} = 90^{0} \Rightarrow KN$ $\widehat{NAK} = 90^{0} \Rightarrow KN$ là đường kính của $(O')$, hay $N,O',K$ thẳng hàng.

B. Hai đường tròn cắt nhau

Xét hai đường tròn $(O;R),(O';R')$

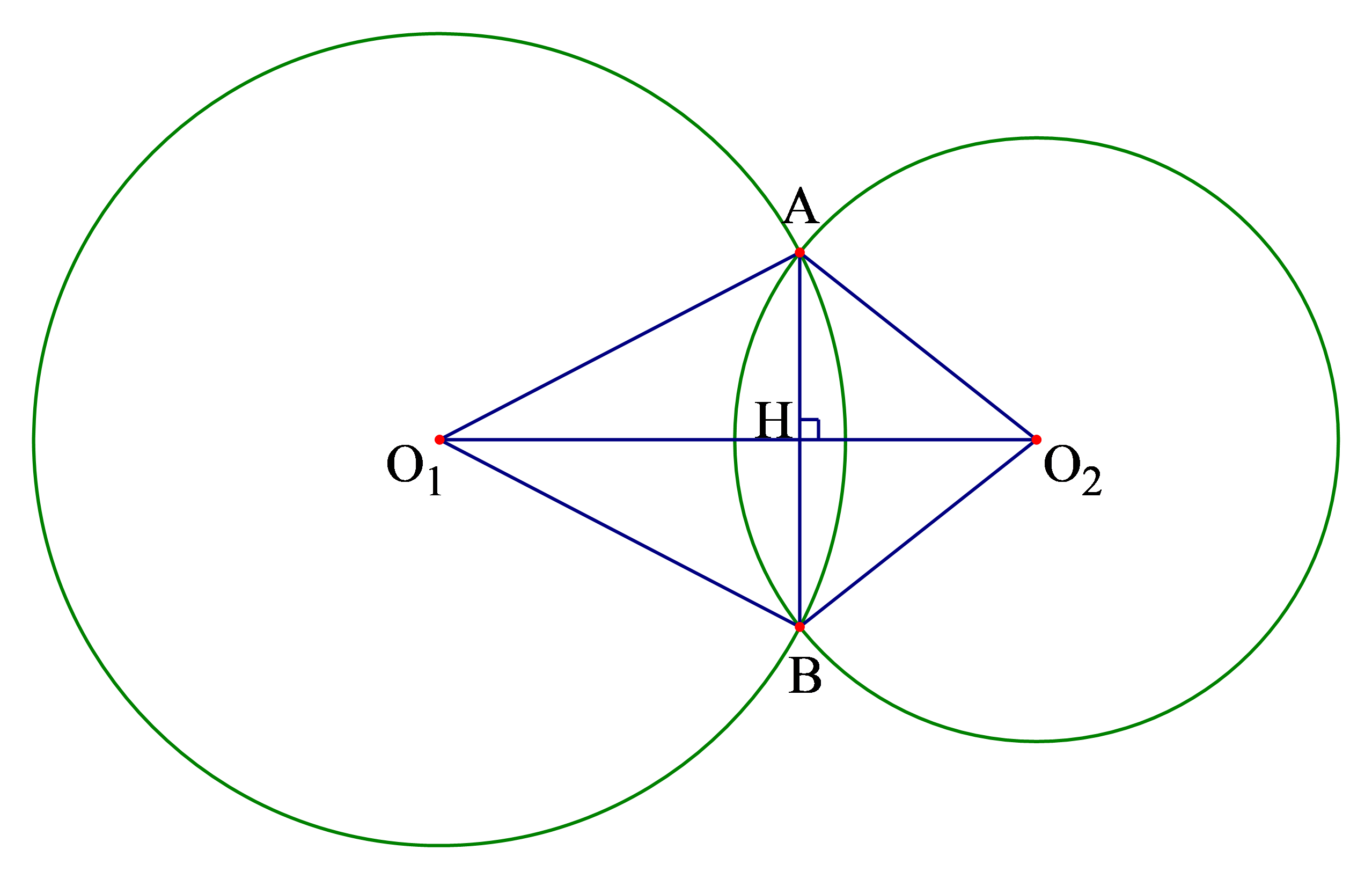
Khi hai đường tròn $(O_{1}),(O_{2})$ $(O_{1}),(O_{2})$cắt nhau theo dây $AB$ thì $O_{1}O_{2}\bot AB$ $O_{1}O_{2}\bot AB$ tại trung điểm $H$ của $AB$. Hay $AB$ là đường trung trực của $O_{1}O_{2}$ $O_{1}O_{2}$

Khi giải toán liên quan dây cung của đường tròn, hoặc cát tuyến ta cần chú ý kẻ thêm đường phụ là đường vuông góc từ tâm đến các dây cung.

Ví dụ. Cho hai đường tròn $(O_{1};R),(O_{2};R)$ $(O_{1};R),(O_{2};R)$ cắt nhau tại $A,B$( $O_{1},O_{2}$ $O_{1},O_{2}$ nằm khác phía so với đường thẳng $AB$). Một cát tuyến $PAQ$ xoay quanh $A$ $\left( P \in \left( O_{1} \right),Q \in \left( O_{2} \right) \right)$ $\left( P \in \left( O_{1} \right),Q \in \left( O_{2} \right) \right)$ sao cho $A$ nằm giữa $P$ và $Q$. Hãy xác đinh vị trí của cát tuyến $PAQ$ trong mỗi trường hợp.

a. $A$ là trung điểm của $PQ$

b. $PQ$ có độ dài lớn nhất

c. Chu vi tam giác $BPQ$ lớn nhất

d. $S_{\Delta BPQ}$ $S_{\Delta BPQ}$ lớn nhất.

Lời giải:

Hình vẽ minh họa

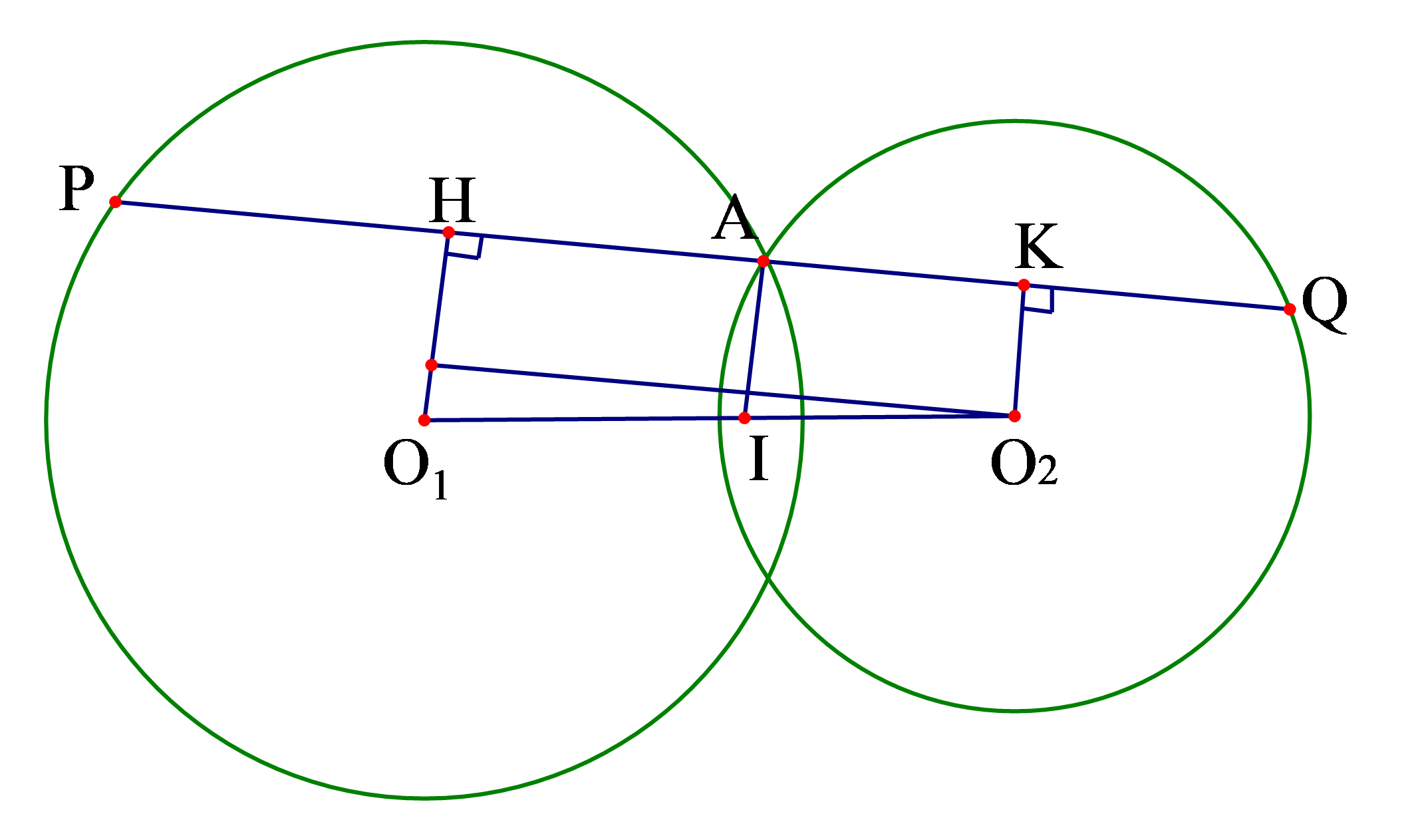
a) Giả sử đã xác định được vị trí của cát tuyến $PAQ$ sao cho $PA = AQ$.

Kẻ $O_{1}H$ $O_{1}H$ vuông góc với dây $PA$ thì $PH = HA = \frac{1}{2}PA$ $PH = HA = \frac{1}{2}PA$.

Kẻ $O_{2}K$ $O_{2}K$ vuông góc với dây $AQ$ thì $AK = KQ = \frac{1}{2}AQ$ $AK = KQ = \frac{1}{2}AQ$.

Nên $AH = AK$.

Kẻ $Ax//O,H//O_{2}K$ $Ax//O,H//O_{2}K$ cắt $O$, $O_{2}$ $O_{2}$ tại $I$ thì $O_{1}I = IO_{2}$ $O_{1}I = IO_{2}$ và $Ax\bot PQ$ $Ax\bot PQ$.

Từ đó suy ra cách xác định vị trí của cát tuyến $PAQ$ đó là cát tuyến $PAQ$ vuông góc với $IA$ tại $A$ với $I$ là trung điểm của đoạn nối tâm $O_{1}O_{2}$ $O_{1}O_{2}$.

b) Trên hình, ta thấy $PA = HK$.

Kẻ $O_{2}M\bot O_{1}H$ $O_{2}M\bot O_{1}H$ thì tứ giác $MHKO_{2}$ $MHKO_{2}$ có ba góc vuông nên là hình chữ nhật do đó $HK = MO_{2}$ $HK = MO_{2}$. Lúc đó $O_{2}M$ $O_{2}M$ là đường vuông góc kẻ từ $O_{2}$ $O_{2}$ đến đường thẳng $O_{1}H,O_{2}O_{1}$ $O_{1}H,O_{2}O_{1}$ là đường xiên kẻ từ $O_{2}$ $O_{2}$ đến đường thẳng $O_{1}H$ $O_{1}H$.

Nên $O_{2}M \leq O_{1}O_{2}$ $O_{2}M \leq O_{1}O_{2}$ hay $PQ = 2HK = 2O_{2}M \leq 2O_{1}O_{2}$ $PQ = 2HK = 2O_{2}M \leq 2O_{1}O_{2}$ (không đổi). dấu đẳng thức xảy ra $\Leftrightarrow M \equiv O$ $\Leftrightarrow M \equiv O$ hay $PQ//O_{1}O_{2}$ $PQ//O_{1}O_{2}$. Vậy ở vị trí cát tuyến $PAQ//O_{1}O_{2}$ $PAQ//O_{1}O_{2}$ thì $PQ$ có độ dài lớn nhất.

c) Qua $A$ kẻ cát tuyến $CAD$ vuông góc với $BA$.

Thì tam giác $ABC$ và $ABD$ vuông tại $A$ lần lượt nội tiếp các đường tròn $\left( O_{1} \right)$ $\left( O_{1} \right)$, $\left( O_{2} \right)$ $\left( O_{2} \right)$ nên $O_{1}$ $O_{1}$ là trung điểm của $BC$ và $O_{2}$ $O_{2}$ là trung điểm của $BD$.

Lúc đó $O_{1}O_{2}$ $O_{1}O_{2}$ là đường trung bình của tam giác $BCD$ nên $O_{1}O_{2}//CD$ $O_{1}O_{2}//CD$ suy ra $PQ \leq 2O_{1}O_{2}$ $PQ \leq 2O_{1}O_{2}$ (1) (theo câu b). Lại có $BQ \leq BD$ $BQ \leq BD$ (2), $BP \leq BC$ $BP \leq BC$ (3).

Từ (1), (2), (3) suy ra chu vi tam giác $BPQ,C = PQ + BQ + BP \leq 2\left( O_{1}O_{2} + R_{1} + R_{2} \right)$ $BPQ,C = PQ + BQ + BP \leq 2\left( O_{1}O_{2} + R_{1} + R_{2} \right)$ (không đổi).

Dấu bằng có khi $P \equiv C,Q \equiv D$ $P \equiv C,Q \equiv D$.

Vậy chu vi tam giác $BPQ$ đạt giá trị lớn nhất khi cát tuyến $PAQ$ vuông góc với dây $BA$ tại $A$.

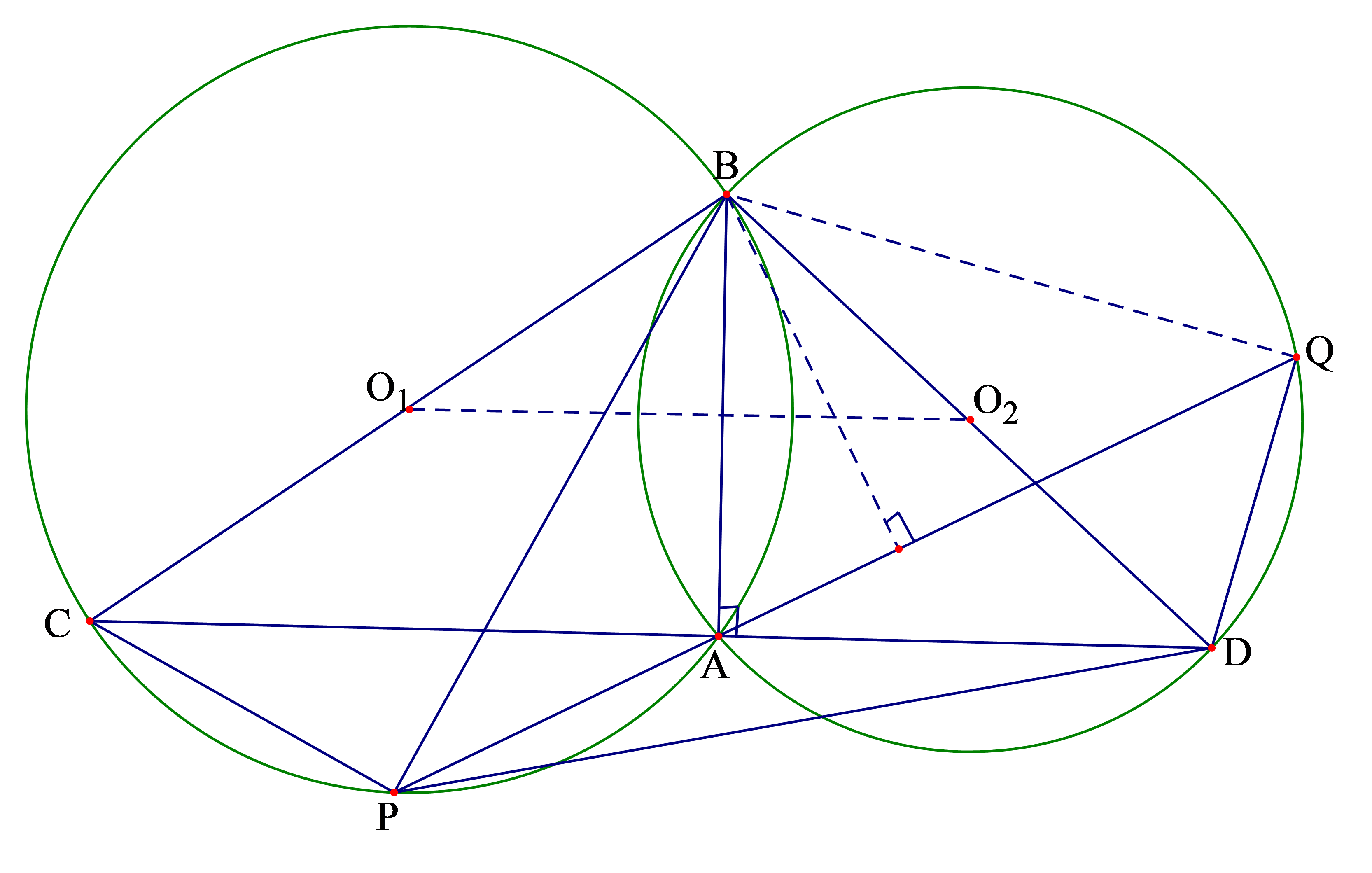
d) Kẻ $BN\bot PQ$ $BN\bot PQ$ thì $BN \leq BA$ $BN \leq BA$.

Lúc đó $S_{BPQ} = \frac{1}{2}BN.PQ \leq \frac{1}{2}BA.CD$ $S_{BPQ} = \frac{1}{2}BN.PQ \leq \frac{1}{2}BA.CD$ không đổi.

Vậy $S_{BPQ}$ $S_{BPQ}$ đạt giá trị lớn nhất khi cát tuyến $PAQ$ vuông góc với dây chung $BA$ tại $A$.

C. Bài tập tự rèn luyện có đáp án

Bài 1. Cho hai đường tròn $(O;R)$ và $(O';R')$ tiếp xúc ngoài tại $A$với $(R > R')$. Đường nối tâm $OO'$cắt $(O),(O')$ lần lượt tại $B,C$. Dây $DE$ của $(O)$ vuông góc với $BC$ tại trung điểm $K$ của $BC$

a. Chứng minh $BDCE$ là hình thoi

b. Gọi $I$ là giao điểm của $EC$ và $(O')$. Chứng minh $D,A,I$ thẳng hàng

c. Chứng minh $KI$ là tiếp tuyến của $(O')$.

Bài 2. Chứng minh rằng: Trong một tam giác tâm vòng tròn ngoại tiếp $O$trọng tâm $G$trực tâm $H$ nằm trên một đường thẳng và $HG = 2GO$(Đường thẳng Ơ le) . Gọi $R,r,d$ lần lượt là bán kính vòng tròn ngoại tiếp nội tiếp và khoảng cách giữa hai tâm chứng minh $d^{2} = R^{2} - r^{2}$ $d^{2} = R^{2} - r^{2}$ (Hệ thức Ơ le).

Bài 3. Cho hai đường tròn $(O_{1};R),(O_{2};R)$ $(O_{1};R),(O_{2};R)$ cắt nhau tại đường thẳng $O_{1}H$ $O_{1}H$ cắt $\left( O_{1} \right)$ $\left( O_{1} \right)$ tại $K,$cắt $(O_{2})$ $(O_{2})$ tại $B$ , $O_{2}H$ $O_{2}H$ cắt $\left( O_{1} \right)$ $\left( O_{1} \right)$ tại $C,$cắt $(O_{2})$ $(O_{2})$ tại $D$. Chứng minh ba đường thẳng $BC,BD,HK$ đồng quy tại một điểm.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

----------------------------------------------------

Hy vọng với chuyên đề vị trí tương đối của hai đường tròn được trình bày khoa học và có lời giải cụ thể, học sinh sẽ củng cố kiến thức hình học vững vàng, rèn luyện tư duy logic và đạt điểm cao trong kỳ thi tuyển sinh lớp 10. Hãy kiên trì luyện tập và ứng dụng linh hoạt các phương pháp giải để làm chủ chuyên đề này!

Tải về

Chọn file muốn tải về: