VnDoc.com

Chứng minh các điểm cùng thuộc một đường tròn

Chuyên đề Toán 9 ôn thi vào 10 nâng cao

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề Toán 9: Chứng minh các điểm cùng nằm trên một đường tròn

A. Cách chứng minh các điểm cùng nằm trên một đường tròn
- Cách xác định tâm đường tròn
- Cách chứng minh các điểm cùng nằm trên đường tròn
B. Bài tập chứng minh các điểm cùng thuộc đường tròn
C. Bài tập tự rèn luyện có đáp án
- Đáp án bài tập tự rèn luyện

Trong chương trình Toán 9, chuyên đề chứng minh các điểm cùng thuộc một đường tròn đóng vai trò quan trọng trong việc phát triển tư duy hình học và rèn luyện kỹ năng lập luận chặt chẽ. Đây là dạng bài thường gặp trong đề thi vào lớp 10, đặc biệt ở các câu hỏi vận dụng – vận dụng cao. Tài liệu dưới đây giúp học sinh ôn tập chuyên sâu, qua hệ thống bài tập chọn lọc có lời giải chi tiết, bám sát cấu trúc đề thi, hỗ trợ học sinh chinh phục điểm cao môn Toán.

A. Cách chứng minh các điểm cùng nằm trên một đường tròn

Định nghĩa: Đường tròn tâm $O$bán kính $R > 0$ là hình gồm các điểm cách điểm $O$một khoảng $R$ kí hiệu là $(O;R)$ hay $(O)$

+ Đường tròn đi qua các điểm $A_{1},A_{2},...,A_{n}$ $A_{1},A_{2},...,A_{n}$gọi là đường tròn ngoại tiếp đa giác $A_{1}A_{2}...A_{n}$ $A_{1}A_{2}...A_{n}$

+ Đường tròn tiếp xúc với tất cả các cạnh của đa giác $A_{1}A_{2}...A_{n}$ $A_{1}A_{2}...A_{n}$ gọi là đường tròn nội tiếp đa giác đó.

Cách xác định tâm đường tròn

+ Trong tam giác vuông trung điểm cạnh huyền là tâm vòng tròn ngoại tiếp

+ Trong tam giác đều, tâm vòng tròn ngoại tiếp là trọng tâm tam giác đó.

+ Trong tam giác thường:

Tâm vòng tròn ngoại tiếp là giao điểm của 3 đường trung trực của 3 cạnh tam giác đó
Tâm vòng tròn nội tiếp là giao điểm 3 đường phân giác trong của tam giác đó
Phương pháp chứng minh nhiều điểm cùng nằm trên một đường tròn

Cách chứng minh các điểm cùng nằm trên đường tròn

Để chứng minh các điểm $A_{1},A_{2},...,A_{n}$ $A_{1},A_{2},...,A_{n}$ cùng thuộc một đường tròn ta chứng minh các điểm $A_{1},A_{2},...,A_{n}$ $A_{1},A_{2},...,A_{n}$ cách đều điểm $O$ cho trước.

B. Bài tập chứng minh các điểm cùng thuộc đường tròn

Ví dụ 1. Cho tam giác đều $ABC$ có cạnh bằng $a$. $AM,BN,CP$ là các đường trung tuyến. Chứng minh 4 điểm $B,P,N,C$ cùng thuộc một đường tròn. Tính bán kính đường tròn đó.

Hướng dẫn giải

Hình vẽ minh họa

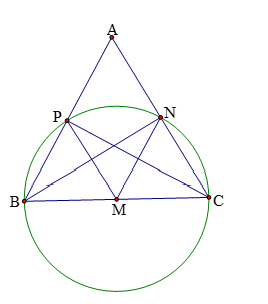
Vì tam giác $ABC$ đều nên các trung tuyến đồng thời cũng là đường cao.

Suy ra $AM,BN,CP$ lần lượt vuông góc với $BC,AC,AB$.

Từ đó ta có các tam giác $BPC,BNC$ là tam giác vuông

Với $BC$ là cạnh huyền, suy ra $MP = MN = MB = MC$

Hay: Các điểm $B,P,N,C$ cùng thuộc đường tròn

Đường kính $BC = a$, tâm đường tròn là

Trung điểm $M$của $BC$.

Ví dụ 2. Cho tứ giác $ABCD$ có $\widehat{C} + \widehat{D} = 90^{0}.$ $\widehat{C} + \widehat{D} = 90^{0}.$ Gọi $M,N,P,Q$ lần lượt là trung điểm của $AB,BD,DC,CA$. Chứng minh 4 điểm $M,N,P,Q$ cùng thuộc một đường tròn. Tìm tâm đường tròn đó.

Hướng dẫn giải:

Hình vẽ minh họa

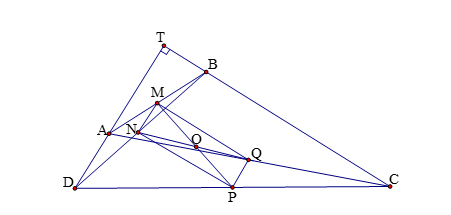
Kéo dài $AD,CB$ cắt nhau tại điểm $T$ thì tam giác $TCD$ vuông tại $T$.

+ Do $MN$ là đường trung bình của tam giác $ABD$ nên $NM//AD$

+ $MQ$ là đường trung bình của tam giác $ABC$ nên $MQ//BC$. Mặt khác $AD\bot BC \Rightarrow MN\bot MQ$ $AD\bot BC \Rightarrow MN\bot MQ$.

Chứng minh tương tự ta cũng có: $MN\bot NP,NP\bot PQ$ $MN\bot NP,NP\bot PQ$. Suy ra $MNPQ$ là hình chữ nhật.

Hay các điểm $M,N,P,Q$ thuộc một đường tròn có tâm là giao điểm $O$ của hai đường chéo $NQ,MP$

Ví dụ 3. Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $(O)$. Gọi $M$ là trung điểm của $AC$. Điểm $G$ là trọng tâm của tam giác $ABM$. Gọi $Q$ là giao điểm của $BM$ và $GO$. Xác định tâm đường tròn ngoại tiếp tam giác $BGQ$.

Hướng dẫn giải

Hình vẽ minh họa

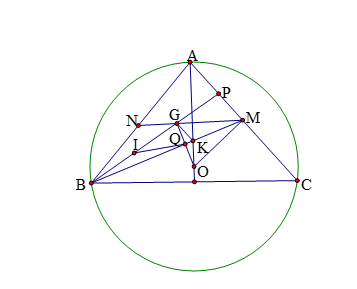
Vì tam giác $ABC$ cân tại $A$ nên tâm $O$ của vòng tròn ngoại tiếp tam giác nằm trên đường trung trực của $BC$.Gọi $K$ là giao điểm của $AO$ và $BM$

Dưng các đường trung tuyến $MN,BP$ của tam giác $ABM$ cắt nhau tại trọng tâm $G$.

Do $MN//BC \Rightarrow MN\bot AO$ $MN//BC \Rightarrow MN\bot AO$. Gọi $K$là giao điểm của $BM$ và $AO$ thì $K$ là trọng tâm của tam giác $ABC$ suy ra $GK//AC$.

Mặt khác ta có $OM\bot AC$ $OM\bot AC$ suy ra $GK\bot OM$ $GK\bot OM$ hay $K$ là trực tâm của tam giác $OMG \Rightarrow MK\bot OG$ $OMG \Rightarrow MK\bot OG$.

Như vậy tam giác $BQG$ vuông tại $Q$. Do đó tâm vòng tròn ngoại tiếp tam giác $GQB$ là trung điểm $I$ của $BG$.

Ví dụ 4. Cho hình thang vuông $ABCD$ có $\widehat{A} = \widehat{B} = 90^{0}$ $\widehat{A} = \widehat{B} = 90^{0}$.$BC = 2AD = 2a$. Gọi $H$ là hình chiếu vuông góc của $B$ lên $AC$. Điểm $M$ là trung điểm của $HC$. Tìm tâm và bán kính đường tròn ngoại tiếp tam giác $BDM$.

Hướng dẫn giải

Hình vẽ minh họa:

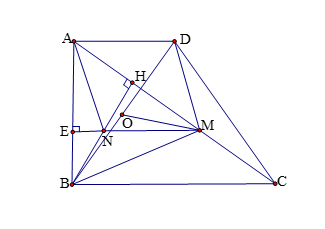
Gọi $N$ là trung điểm của $BH$ thì $MN$ là đường trung bình của tam giác $HBC$ suy ra $MN\bot AB$ $MN\bot AB$, mặt khác $BH\bot AM \Rightarrow N$ $BH\bot AM \Rightarrow N$ là trực tâm của tam giác $ABM$ suy ra $AN\bot BM$ $AN\bot BM$.

Do $MN// = \frac{1}{2}BC \Rightarrow MN// = AD$ $MN// = \frac{1}{2}BC \Rightarrow MN// = AD$ nên $ADMN$ là hình bình hành suy ra $AN//DM$.

Từ đó ta có: $DM\bot BM$ $DM\bot BM$ hay tam giác $DBM$ vuông tại $M$ nên tâm vòng tròn ngoại tiếp tam giác $DBM$ là trung điểm$O$ của $BD$.

Ta có

$R = MO = \frac{1}{2}BD =\frac{1}{2}\sqrt{AB^{2} + AD^{2}}$ $R = MO = \frac{1}{2}BD =\frac{1}{2}\sqrt{AB^{2} + AD^{2}}$ $= \frac{1}{2}\sqrt{4a^{2} + a^{2}} =\frac{a\sqrt{5}}{2}$ $= \frac{1}{2}\sqrt{4a^{2} + a^{2}} =\frac{a\sqrt{5}}{2}$.

C. Bài tập tự rèn luyện có đáp án

Bài tập 1. Cho lục giác đều $ABCDEF$ tâm $O$. Gọi $M,N$ là trung điểm của $CD,DE$. $AM$ cắt $BN$ tại $I$. Chứng minh rằng các điểm $M,I,O,N,D$ nằm trên một đường tròn.

Bài tập 2. Cho hình vuông $ABCD$. Gọi $M$ là trung điểm $BC,N$ là điểm thuộc đường chéo $AC$ sao cho $AN = \frac{1}{4}AC$ $AN = \frac{1}{4}AC$. Chứng minh 4 điểm $M,N,C,D$ nằm trên cùng một đường tròn.

Bài tập 3. Trong tam giác $ABC$ gọi $M,N,P$ lần lượt là trung điểm của $AB,BC,CA$. Các điểm $A_{1},B_{1},C_{1}$ $A_{1},B_{1},C_{1}$ lần lượt là các chân đường cao hạ từ đỉnh $A,B,C$ đến các cạnh đối diện. $A_{2},B_{2},C_{2}$ $A_{2},B_{2},C_{2}$ là trung điểm của $HA,HB,HC$. Khi đó $9$ điểm $M,N,P,A_{1},B_{1},C_{1},A_{2},B_{2},C_{2}$ $M,N,P,A_{1},B_{1},C_{1},A_{2},B_{2},C_{2}$ cùng nằm trên một đường tròn gọi là đường tròn Ơ le của tam giác.

Bài tập 4. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, $AD$ là đường kính của $(O)$. $M$ là trung điểm của $BC,H$ là trực tâm của tam giác. Gọi $X,Y,Z$ lần lượt là hình chiếu vuông góc của điểm $D$ lên $HB,HC,BC$. Chứng minh 4 điểm $X,Y,Z,M$ cùng thuộc một đường tròn.

Bài tập 5. Cho tam giác $ABC$ có trực tâm $H$. Lấy điểm $M,N$ thuộc tia $BC$ sao cho $MN = BC$ và $M$ nằm giữa $B,C$. Gọi $D,E$ lần lượt là hình chiếu vuông góc của $M,N$ lên $AC,AB$. Chứng minh các điểm $A,D,E,H$ cùng thuộc một đường tròn.

Bài tập 6. Cho tam giác $ABC$, $P$ là điểm bất kỳ $PA,PB,PC$ cắt đường tròn ngoại tiếp tam giác $ABC$ tại $A_{1},B_{1},C_{1}$ $A_{1},B_{1},C_{1}$. Gọi $A_{2},B_{2},C_{2}$ $A_{2},B_{2},C_{2}$ là các điểm đối xứng với $A_{1},B_{1},C_{1}$ $A_{1},B_{1},C_{1}$ qua trung điểm của $BC,CA,AB$. Chứng minh rằng: $A_{2},B_{2},C_{2}$ $A_{2},B_{2},C_{2}$ và trực tâm $H$ của tam giác $ABC$ cùng thuộc một đường tròn.

Đáp án bài tập tự rèn luyện

Bài tập 1

Hình vẽ minh họa:

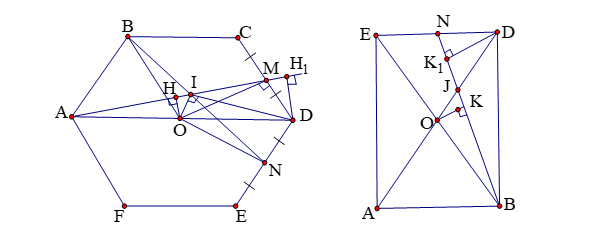
Do $ABCDEF$ là lục giác đều nên $OM\bot CD,ON\bot DE$ $OM\bot CD,ON\bot DE$

$\Rightarrow M,N,C,D$ $\Rightarrow M,N,C,D$ nằm trên đường tròn đường kính $OD$.

Vì tam giác $\Delta OBN = \Delta OAM$ $\Delta OBN = \Delta OAM$ nên điểm $O$ cách đều $AM,BN$ suy ra $OI$ là phân giác trong của góc $\widehat{AIN}$ $\widehat{AIN}$.

Kẻ $\left\{ \begin{matrix} OH\bot AM \\ DH_{1}\bot AM \end{matrix} \right.\ \Rightarrow DH_{1} = 2OH$ $\left\{ \begin{matrix} OH\bot AM \\ DH_{1}\bot AM \end{matrix} \right.\ \Rightarrow DH_{1} = 2OH$ (Do $OH$ là đường trung bình của tam giác $DAH_{1}$ $DAH_{1}$

Kẻ $\left\{ \begin{matrix} OK\bot BN \\ DK_{1}\bot BN \end{matrix} \right.\ \Rightarrow DK_{1} = 2OK$ $\left\{ \begin{matrix} OK\bot BN \\ DK_{1}\bot BN \end{matrix} \right.\ \Rightarrow DK_{1} = 2OK$ (Do $\frac{OK}{DK_{1}} = \frac{JO}{JD} = \frac{1}{2}$ $\frac{OK}{DK_{1}} = \frac{JO}{JD} = \frac{1}{2}$ với $J = AD \cap NB$ $J = AD \cap NB$)

Do $OK = OH \Leftrightarrow DH_{1} = DK_{1}$ $OK = OH \Leftrightarrow DH_{1} = DK_{1}$ suy ra $D$ cách đều $AM,BN$ hay $ID$ là phân giác ngoài của $\widehat{AIN} \Rightarrow \widehat{OID} = 90^{0}$ $\widehat{AIN} \Rightarrow \widehat{OID} = 90^{0}$.

Vậy 5 điểm $M,I,O,N,D$ cùng nằm trên một đường tròn đường kính $OD$.

Bài tập 2.

Ta thấy tứ giác $MCDN$ có $\widehat{MCD} = 90^{0}$ $\widehat{MCD} = 90^{0}$ nên để chứng minh 4 điểm $M,N,C,D$ cùng nằm trên một đường tròn ta sẽ chứng minh $\widehat{MND} = 90^{0}$ $\widehat{MND} = 90^{0}$.

Cách 1: Kẻ đường thẳng qua $N$ song song với $AB$ cắt $BC,AD$ tại $E,F$.

Xét hai tam giác vuông $NEM$ và $DFN$ $EM = NF = \frac{1}{4}AB,EN = DF = \frac{1}{4}AB$ $EM = NF = \frac{1}{4}AB,EN = DF = \frac{1}{4}AB$ từ đó suy ra $\Delta NEM = \Delta DFN$ $\Delta NEM = \Delta DFN$

Do đó $\widehat{NME} = \widehat{DNF},\widehat{MNE} = \widehat{NDF} \Rightarrow \widehat{MNE} + \widehat{DNF} = 90^{0}$ $\widehat{NME} = \widehat{DNF},\widehat{MNE} = \widehat{NDF} \Rightarrow \widehat{MNE} + \widehat{DNF} = 90^{0}$

Hay tam giác $MND$ vuông tại $N$. Suy ra 4 điểm $M,N,C,D$ cùng nằm trên đường tròn đường kính $MD$.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

-------------------------------------

Với những dạng bài chứng minh điểm cùng thuộc một đường tròn điển hình và hướng dẫn giải cụ thể, chuyên đề này sẽ là hành trang vững chắc cho học sinh lớp 9 trong quá trình ôn thi vào lớp 10. Hãy luyện tập đều đặn để nắm vững kỹ năng hình học và tự tin bước vào kỳ thi quan trọng sắp tới.

Mời bạn đọc tham khảo thêm một số tài liệu đặc sắc của chúng tôi:

Tải về

Chọn file muốn tải về: