VnDoc.com

63 đề thi tuyển sinh lớp 10 môn Toán

Đề thi vào lớp 10 môn Toán có đáp án

Tải về

             

            

            

      

  

  21 tháng 6 năm 2012

   : 120 phút

  (2,5 điểm)

   

 



 







         

    

   

 

     

 



 

 

  

 



   



                       

      

  (2,0 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

        





         

                     

            

  (1,5 điểm)

    

 



 

 



 



 







 





    



     



            

   



 



   

 

 

   

  (3,5 điểm)

                   

                       

        

  



 

                    

   

  

             

            

                        

        









        

    

  (0,5 điểm)           

 

       



 

 









    

   

        

36 4 10 5

8 4

36 2



 



  



     

 

x( x 4) 4( x 4) x 2

x 16 x 16 x 16

 

  



 

  

 



(x 16)( x 2) x 2

(x 16)(x 16) x 16

  



  

  

2 4 2 2 2

( 1) . 1 .

16 16 16

2 2

x x x

B A

x x x

x x

 

  

    

 

  

 

 





( 1)B A 

   

16x 

      





  

      

16x 



1



2











  

0, 16x x 

 

( 1)B A 

 





 x 

   

                

12

5

x 

                

      

1

x

     

1

2x 



         





        















     

             

            

1 1 5

x x 2 12

 



 

  

x x

 

 









     

      



 



 

 

7 13 6

5 5

x

 



  

7 13 20

4

5 5

x



          

           

     

2 1

2

6 2

1

x y



 







 





 

, 0x y 





4 2

4 6 10

4

2

4 1 5

2

2 1

2 1 2 1

2

6 2 1

2 2

1

2

x

x y

x x x

y

x y x y

x y



 

 



   





 





   

    

    

 





   

   

 



  

 





    

           



 



   



    

        

      

1 2

2

1 2

4 1

3 2

x x m

x x m m

  







 







 

2 2 2

1 2 1 2 1 2

7 ( ) 2 7x x x x x x     



  



 



   







     







     

                   

3

5





  

   

















Đề thi tuyển sinh lớp 10 môn Toán

Tổng hợp 63 đề thi tuyển sinh vào lớp 10 được VnDoc sưu tầm và đăng tải nhằm giúp các bạn học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

SỞ GIÁO DỤC VÀ ĐÀO TẠO

HÀ NỘI

KỲ THI TUYỂN SINH LỚP 10 THPT

Năm học:

Môn thi: Toán

Ngày thi: 21 tháng 6 năm 20

Thời gian làm bài: 120 phút

Bài I (2,5 điểm)

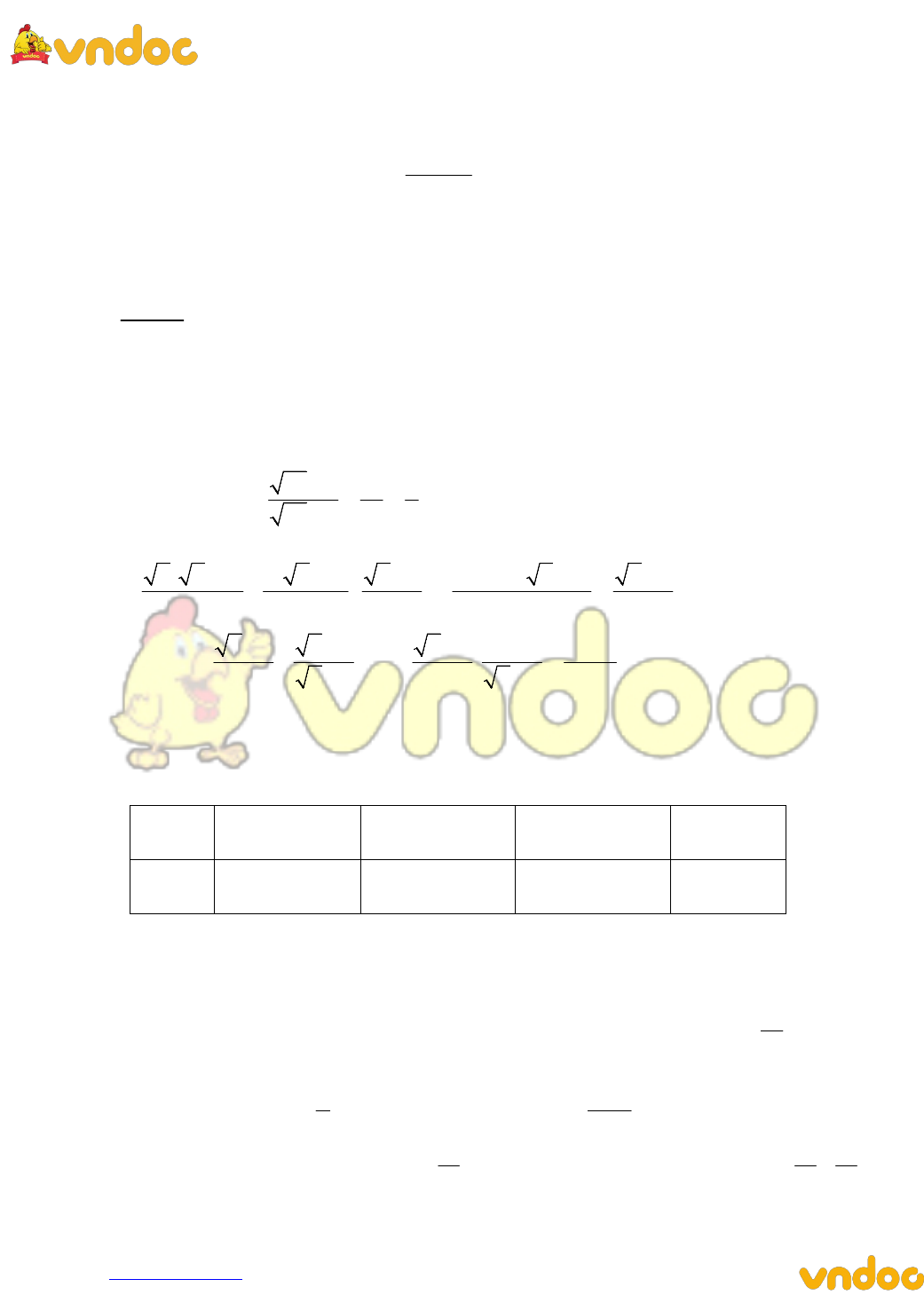
1) Cho biểu thức $A = \frac{{\sqrt x + 4}}{{\sqrt x + 2}}$ $A = \frac{{\sqrt x + 4}}{{\sqrt x + 2}}$. Tính giá trị của A khi x = 36

2) Rút gọn biểu thức $B = \left( {\frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{4}{{\sqrt x - 4}}} \right):\frac{{x + 16}}{{\sqrt x + 2}}$ $B = \left( {\frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{4}{{\sqrt x - 4}}} \right):\frac{{x + 16}}{{\sqrt x + 2}}$(với $x \ge 0;x \ne 16$ $x \ge 0;x \ne 16$)

3) Với các của biểu thức A và B nói trên, hãy tìm các giá trị của x nguyên để giá trị của biểu thức B(A – 1) là số nguyên

Bài II (2,0 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Hai người cùng làm chung một công việc trong giờ thì xong $\frac{{12}}{5}$ $\frac{{12}}{5}$. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành công việc trong ít hơn người thứ hai là 2 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu thời gian để xong công việc?

Bài III (1,5 điểm)

1) Giải hệ phương trình: $\left\{ \begin{array}{l} \frac{2}{x} + \frac{1}{y} = 2\\ \frac{6}{x} - \frac{2}{y} = 1 \end{array} \right.$ $\left\{ \begin{array}{l} \frac{2}{x} + \frac{1}{y} = 2\\ \frac{6}{x} - \frac{2}{y} = 1 \end{array} \right.$

2) Cho phương trình: x² – (4m – 1)x + 3m² – 2m = 0 (ẩn x). Tìm m để phương trình có hai nghiệm phân biệt x₁, x₂ thỏa mãn điều kiện: $x_1^2 + x_2^2 = 7$

Bài IV (3,5 điểm)

Cho đường tròn (O; R) có đường kính AB. Bán kính CO vuông góc với AB, M là một điểm bất kỳ trên cung nhỏ AC (M khác A, C); BM cắt AC tại H. Gọi K là hình chiếu của H trên AB.

1) Chứng minh CBKH là tứ giác nội tiếp.

2) Chứng minh $\widehat {ACM} = \widehat {ACK}$ $\widehat {ACM} = \widehat {ACK}$

3) Trên đọan thẳng BM lấy điểm E sao cho BE = AM. Chứng minh tam giác ECM là tam giác vuông cân tại C

4) Gọi d là tiếp tuyến của (O) tại điểm A; cho P là điểm nằm trên d sao cho hai điểm P, C nằm trong cùng một nửa mặt phẳng bờ AB và $\frac{{AP.MB}}{{MA}} = R$ $\frac{{AP.MB}}{{MA}} = R$. Chứng minh đường thẳng PB đi qua trung điểm của đoạn thẳng HK

Bài V (0,5 điểm). Với x, y là các số dương thỏa mãn điều kiện $x \ge 2y$ $x \ge 2y$, tìm giá trị nhỏ nhất của biểu thức: $M = \frac{{{x^2} + {y^2}}}{{xy}}$ $M = \frac{{{x^2} + {y^2}}}{{xy}}$

Để xem full đề + đáp án, mời các bạn tải về nhé!

Tổng hợp 63 đề thi tuyển sinh vào lớp 10 được VnDoc chia sẻ trên đây gồm các đề thi tuyển sinh vào lớp 10 của các tỉnh trên cả nước, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi thử trên đây các bạn tham khảo các đề của các tỉnh khác nữa nhé

............................................

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Tổng hợp 63 đề thi tuyển sinh vào lớp 10. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết được tổng hợp các mã đề thi tuyển sinh vào lớp 10. Hi vọng qua bài viết bạn đọc có thêm nhiều tài liệu để học tập tốt hơn nhé.

Tham khảo thêm

Chia sẻ, đánh giá bài viết

42

44.313

Chia sẻ bởi:
Đinh Thị Nhàn
Nhóm:
Sưu tầm
Ngày: 22/05/2023

Tải về

Chọn file muốn tải về: