VnDoc.com

Tìm giá trị lớn nhất, nhỏ nhất của các biểu thức hình học

Chuyên đề ôn Toán 9 thi vào 10 Có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Dạng tài liệu: Chuyên đề

Mức độ: Khó

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập Toán 9: Tìm giá trị lớn nhất, giá trị nhỏ nhất hình học

Trong quá trình học và ôn luyện Toán THPT, dạng bài tìm giá trị lớn nhất, nhỏ nhất của các biểu thức hình học là một trong những dạng toán quan trọng, thường xuyên xuất hiện trong các đề thi học kỳ và kỳ thi tuyển sinh vào lớp 10 môn Toán . Bài viết dưới đây sẽ giúp bạn hệ thống lại các dạng bài phổ biến, hướng dẫn phương pháp giải hiệu quả, cùng ví dụ minh họa có lời giải chi tiết, giúp học sinh rèn luyện tư duy phân tích và làm bài chính xác.

I. Bất đẳng thức cần nhớ

a) Cho các số thực dương $a,b$

$a + b \geq 2\sqrt{ab} \Leftrightarrow ab \leq \left( \frac{a + b}{2} \right)^{2} \Leftrightarrow (a + b)^{2} \geq 4ab$ $a + b \geq 2\sqrt{ab} \Leftrightarrow ab \leq \left( \frac{a + b}{2} \right)^{2} \Leftrightarrow (a + b)^{2} \geq 4ab$

Dấu bằng xảy ra khi và chỉ khi $a = b$

$\frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b} \geq \frac{2\sqrt{2}}{\sqrt{a^{2} + b^{2}}}$ $\frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b} \geq \frac{2\sqrt{2}}{\sqrt{a^{2} + b^{2}}}$ ; $\frac{x^{2}}{a} + \frac{y^{2}}{b} \geq \frac{(x + y)^{2}}{a + b}$ $\frac{x^{2}}{a} + \frac{y^{2}}{b} \geq \frac{(x + y)^{2}}{a + b}$
$a^{2} + ab + b^{2} = \frac{3}{4}(a + b)^{2} + \frac{1}{4}(a - b)^{2} \geq \frac{3}{4}(a + b)^{2}$ $a^{2} + ab + b^{2} = \frac{3}{4}(a + b)^{2} + \frac{1}{4}(a - b)^{2} \geq \frac{3}{4}(a + b)^{2}$
$a^{2} - ab + b^{2} = \frac{1}{4}(a + b)^{2} + \frac{3}{4}(a - b)^{2} \geq \frac{1}{4}(a + b)^{2}$ $a^{2} - ab + b^{2} = \frac{1}{4}(a + b)^{2} + \frac{3}{4}(a - b)^{2} \geq \frac{1}{4}(a + b)^{2}$

b) Cho các số thực dương $a,b,c$:

$a + b + c \geq 3\sqrt[3]{abc} \Leftrightarrow abc \leq \left( \frac{a + b + c}{3} \right)^{3}$ $a + b + c \geq 3\sqrt[3]{abc} \Leftrightarrow abc \leq \left( \frac{a + b + c}{3} \right)^{3}$

Dấu bằng xảy ra khi và chỉ khi $a = b = c$

$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq \frac{9}{a + b + c} \geq \frac{3\sqrt{3}}{\sqrt{a^{2} + b^{2} + c^{2}}}$ $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq \frac{9}{a + b + c} \geq \frac{3\sqrt{3}}{\sqrt{a^{2} + b^{2} + c^{2}}}$
$ab + bc + ca \leq \frac{(a + b + c)^{2}}{3} \leq a^{2} + b^{2} + c^{2}$ $ab + bc + ca \leq \frac{(a + b + c)^{2}}{3} \leq a^{2} + b^{2} + c^{2}$
$\frac{x^{2}}{a} + \frac{y^{2}}{b} + \frac{z^{2}}{c} \geq \frac{(x + y + z)^{2}}{a + b + c}$ $\frac{x^{2}}{a} + \frac{y^{2}}{b} + \frac{z^{2}}{c} \geq \frac{(x + y + z)^{2}}{a + b + c}$

II. Bài tập minh họa tìm giá trị lớn nhất nhỏ nhất của các biểu thức hình học

Bài 1. Cho tam giác $ABC$ và một điểm $M$ tùy ý trong tam giác đó. Gọi khoảng cách từ $M$ đến các cạnh $BC,CA,AB$ theo thứ tự là $m,n,p$ và các đường cao hạ từ các đỉnh $A,B,C$ là $h_{a},h_{b},h_{c}$ $h_{a},h_{b},h_{c}$. Chứng minh: $\frac{h_{a}}{m} + \frac{h_{b}}{n} + \frac{h_{c}}{p} \geq 9$ $\frac{h_{a}}{m} + \frac{h_{b}}{n} + \frac{h_{c}}{p} \geq 9$.

Hướng dẫn giải

Hình vẽ minh họa

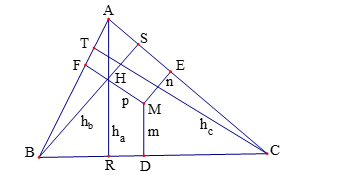
Trước hết ta chứng minh kết quả sau: $\frac{m}{h_{a}} + \frac{n}{h_{b}} + \frac{p}{h_{c}} = 1$ $\frac{m}{h_{a}} + \frac{n}{h_{b}} + \frac{p}{h_{c}} = 1$

Kí hiệu $S_{a},S_{b},S_{c},S$ $S_{a},S_{b},S_{c},S$ lần lượt là diện tích tam giác $MBC,MAC,MAB,ABC$

ta có: $\frac{S_{a}}{S} = \frac{m}{h_{a}},\frac{S_{b}}{S} = \frac{n}{h_{b}},\frac{S_{c}}{S} = \frac{p}{h_{c}}$ $\frac{S_{a}}{S} = \frac{m}{h_{a}},\frac{S_{b}}{S} = \frac{n}{h_{b}},\frac{S_{c}}{S} = \frac{p}{h_{c}}$ suy ra $\frac{m}{h_{a}} + \frac{n}{h_{b}} + \frac{p}{h_{c}} = \frac{S_{a} + S_{b} + S_{c}}{S} = 1$ $\frac{m}{h_{a}} + \frac{n}{h_{b}} + \frac{p}{h_{c}} = \frac{S_{a} + S_{b} + S_{c}}{S} = 1$

Sử dụng bất đẳng thức Cauchy ta dễ chứng minh được kết quả sau (với $(x,y,z > 0)$: $(x + y + z)\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \right) \geq 9$ $(x + y + z)\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \right) \geq 9$.

Áp dụng vào bài toán ta có: $\frac{h_{a}}{m} + \frac{h_{b}}{n} + \frac{h_{c}}{p} \geq \frac{9}{\frac{m}{h_{a}} + \frac{n}{h_{b}} + \frac{p}{h_{c}}} = 9$ $\frac{h_{a}}{m} + \frac{h_{b}}{n} + \frac{h_{c}}{p} \geq \frac{9}{\frac{m}{h_{a}} + \frac{n}{h_{b}} + \frac{p}{h_{c}}} = 9$.

Dấu bằng xảy ra khi và chỉ khi $\frac{h_{a}}{m} = \frac{h_{b}}{n} = \frac{h_{c}}{n} = 3$ $\frac{h_{a}}{m} = \frac{h_{b}}{n} = \frac{h_{c}}{n} = 3$

Hay $M$ là trọng tâm của tam giác $\Delta ABC$ $\Delta ABC$.

Bài 2. Cho tam giác $ABC$ và một điểm $M$ tùy ý trong tam giác đó. Các đường thẳng $AM,BM,CM$ cắt các cạnh $BC,CA,AB$ tại các giao điểm tương ứng là: $A_{1},B_{1},C_{1}$ $A_{1},B_{1},C_{1}$. Kí hiệu $S_{a},S_{b},S_{c},S$ $S_{a},S_{b},S_{c},S$ lần lượt là diện tích tam giác $MBC,MAC,MAB,ABC$ . Chứng minh: $\frac{AA_{1}}{MA_{1}} + \frac{BB_{1}}{MB_{1}} + \frac{CC_{1}}{MC_{1}} \geq 9$ $\frac{AA_{1}}{MA_{1}} + \frac{BB_{1}}{MB_{1}} + \frac{CC_{1}}{MC_{1}} \geq 9$

Hướng dẫn giải

Hình vẽ minh họa

Trước hết ta chứng minh:

$\frac{AA_{1}}{MA_{1}} + \frac{BB_{1}}{MB_{1}} + \frac{CC_{1}}{MC_{1}} = S\left( \frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \right)$ $\frac{AA_{1}}{MA_{1}} + \frac{BB_{1}}{MB_{1}} + \frac{CC_{1}}{MC_{1}} = S\left( \frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \right)$.

Ta có $\frac{AA_{1}}{MA_{1}} = \frac{S_{ABA_{1}}}{S_{MBA_{1}}} = \frac{S_{ACA_{1}}}{S_{MCA_{1}}} = \frac{S_{ABA_{1}} + S_{ACA_{1}}}{S_{MBA_{1}} + S_{MCA_{1}}} = \frac{S}{S_{a}}$ $\frac{AA_{1}}{MA_{1}} = \frac{S_{ABA_{1}}}{S_{MBA_{1}}} = \frac{S_{ACA_{1}}}{S_{MCA_{1}}} = \frac{S_{ABA_{1}} + S_{ACA_{1}}}{S_{MBA_{1}} + S_{MCA_{1}}} = \frac{S}{S_{a}}$,

Tương tự ta có: $\frac{BB_{1}}{MB_{1}} = \frac{S}{S_{b}},\frac{CC_{1}}{MC_{1}} = \frac{S}{S_{c}}$ $\frac{BB_{1}}{MB_{1}} = \frac{S}{S_{b}},\frac{CC_{1}}{MC_{1}} = \frac{S}{S_{c}}$.

Cộng ba đẳng thức ta có: $\frac{AA_{1}}{MA_{1}} + \frac{BB_{1}}{MB_{1}} + \frac{CC_{1}}{MC_{1}} = S\left( \frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \right)$ $\frac{AA_{1}}{MA_{1}} + \frac{BB_{1}}{MB_{1}} + \frac{CC_{1}}{MC_{1}} = S\left( \frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \right)$

Áp dụng bất đẳng thức: $(x + y + z)\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \right) \geq 9$ $(x + y + z)\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \right) \geq 9$ với $(x,y,z > 0)$.

Để ý rằng: $S_{a} + S_{b} + S_{c} = S$ $S_{a} + S_{b} + S_{c} = S$ ta có: $\frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \geq \frac{9}{S_{a} + S_{b} + S_{c}} = \frac{9}{S}$ $\frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \geq \frac{9}{S_{a} + S_{b} + S_{c}} = \frac{9}{S}$ ta có: $S\left( \frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \right) \geq 9$ $S\left( \frac{1}{S_{a}} + \frac{1}{S_{b}} + \frac{1}{S_{c}} \right) \geq 9$.

Dấu bằng xảy ra khi và chỉ khi $S_{a} = S_{b} = S_{c} = \frac{1}{3}S$ $S_{a} = S_{b} = S_{c} = \frac{1}{3}S$. Hay $M$ là trọng tâm của tam giác $\Delta ABC$ $\Delta ABC$.

Chú ý rằng: Từ bài toán trên ta cũng có:

$\frac{MA_{1}}{AA_{1}} = \frac{S_{MBA_{1}}}{S_{ABA_{1}}} = \frac{S_{MCA_{1}}}{S_{ACA_{1}}} = \frac{S_{MBA_{1}} + S_{MCA_{1}}}{S_{ABA_{1}} + S_{ACA_{1}}} = \frac{S_{a}}{S}$ $\frac{MA_{1}}{AA_{1}} = \frac{S_{MBA_{1}}}{S_{ABA_{1}}} = \frac{S_{MCA_{1}}}{S_{ACA_{1}}} = \frac{S_{MBA_{1}} + S_{MCA_{1}}}{S_{ABA_{1}} + S_{ACA_{1}}} = \frac{S_{a}}{S}$.

Tương tự ta có: $\frac{MB_{1}}{BB_{1}} = \frac{S_{b}}{S},\frac{MC_{1}}{CC_{1}} = \frac{S_{c}}{S}$ $\frac{MB_{1}}{BB_{1}} = \frac{S_{b}}{S},\frac{MC_{1}}{CC_{1}} = \frac{S_{c}}{S}$.

Suy ra $\frac{MA_{1}}{AA_{1}} + \frac{MB_{1}}{BB_{1}} + \frac{MC_{1}}{CC_{1}} = \frac{S_{a} + S_{b} + S_{c}}{S} = 1$ $\frac{MA_{1}}{AA_{1}} + \frac{MB_{1}}{BB_{1}} + \frac{MC_{1}}{CC_{1}} = \frac{S_{a} + S_{b} + S_{c}}{S} = 1$

Nếu ta thay: $\frac{MA_{1}}{AA_{1}} =\frac{AA_{1} - MA}{AA_{1}} = 1 - \frac{MA}{AA_{1}},$ $\frac{MA_{1}}{AA_{1}} =\frac{AA_{1} - MA}{AA_{1}} = 1 - \frac{MA}{AA_{1}},$ $\frac{MB_{1}}{BB_{1}}= 1 - \frac{MB}{BB_{1}},$ $\frac{MB_{1}}{BB_{1}}= 1 - \frac{MB}{BB_{1}},$ $\frac{MC_{1}}{CC_{1}} = 1 -\frac{MC}{CC_{1}},$ $\frac{MC_{1}}{CC_{1}} = 1 -\frac{MC}{CC_{1}},$ thì ta thu được đẳng thức: $\frac{MA}{AA_{1}} + \frac{MB}{BB_{1}} + \frac{MC}{CC_{1}} = 2$ $\frac{MA}{AA_{1}} + \frac{MB}{BB_{1}} + \frac{MC}{CC_{1}} = 2$. Qua đó ta cũng tạo ra được nhiều bất đẳng thức đẹp khác.

Bài 3. Trong các tam giác ngoại tiếp đường tròn tâm $O$ bán kính $r$ hãy các định dạng của tam giác sao cho tổng độ dài ba đường cao đạt giá trị nhỏ nhất. Tính giá trị đó.

Hướng dẫn giải

Gọi $h_{a},h_{b},h_{c}$ $h_{a},h_{b},h_{c}$ là độ dài các đường cao tương ứng với các cạnh $a,b,c$ của tam giác $ABC$ ngoại tiếp đường tròn $(O)$.

Ta dễ chứng minh được: $\frac{r}{h_{a}} + \frac{r}{h_{b}} + \frac{r}{h_{c}} = 1$ $\frac{r}{h_{a}} + \frac{r}{h_{b}} + \frac{r}{h_{c}} = 1$.

Áp dụng bất đẳng thức $(x + y + z)\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \right) \geq 9$ $(x + y + z)\left( \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \right) \geq 9$

Ta có $h_{a} + h_{b} + h_{c} = \left( h_{a} + h_{b} + h_{c} \right)\left( \frac{1}{h_{a}} + \frac{1}{h_{b}} + \frac{1}{h_{c}} \right)r \geq 9r$ $h_{a} + h_{b} + h_{c} = \left( h_{a} + h_{b} + h_{c} \right)\left( \frac{1}{h_{a}} + \frac{1}{h_{b}} + \frac{1}{h_{c}} \right)r \geq 9r$.

Đẳng thức xảy ra khi $h_{a} = h_{b} = h_{c} = 3r,h_{a} + h_{b} + h_{c} = 9r$ $h_{a} = h_{b} = h_{c} = 3r,h_{a} + h_{b} + h_{c} = 9r$, lúc đó tam giác $ABC$ đều

III. Bài tập tự rèn luyện có đáp án

Bài 1. Cho tam giác đều $ABC$ có cạnh bằng $a$. Gọi đường vuông góc từ điểm $M$ nằm trong tam giác đến các cạnh $BC,CA,AB$ lần lượt là $MD,ME,MF$. Xác định vị trí điểm $M$để:

a) $\frac{1}{MD} + \frac{1}{ME} + \frac{1}{MF}$ $\frac{1}{MD} + \frac{1}{ME} + \frac{1}{MF}$ đạt giá trị nhỏ nhất. Tính giá trị đó.

b) $\frac{1}{MD + ME} + \frac{1}{ME + MF} + \frac{1}{MF + MD}$ $\frac{1}{MD + ME} + \frac{1}{ME + MF} + \frac{1}{MF + MD}$ đạt giá trị nhỏ nhất. Tính giá trị đó.

Bài 2. Gọi $H$ là trực tâm của tam giác $ABC$ có ba góc nhọn với ba đường cao $AA_{1},BB_{1},CC_{1}$ $AA_{1},BB_{1},CC_{1}$. Chứng minh rằng:

a) $\frac{AA_{1}}{HA_{1}} + \frac{BB_{1}}{HB_{1}} + \frac{CC_{1}}{HC_{1}} \geq 9$ $\frac{AA_{1}}{HA_{1}} + \frac{BB_{1}}{HB_{1}} + \frac{CC_{1}}{HC_{1}} \geq 9$. b) $\frac{HA_{1}}{HA} + \frac{HB_{1}}{HB} + \frac{HC_{1}}{HC} \geq \frac{3}{2}$ $\frac{HA_{1}}{HA} + \frac{HB_{1}}{HB} + \frac{HC_{1}}{HC} \geq \frac{3}{2}$.

Bài 3. Xét tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $(O)$ với ba đường cao $AA_{1},BB_{1},CC_{1}$ $AA_{1},BB_{1},CC_{1}$ lần lượt cắt đường tròn $(O)$ lần nữa tại $D,E,F$. Xác định dạng của tam giác $ABC$ sao cho:

a) $\frac{AA_{1}}{DA_{1}} + \frac{BB_{1}}{EB_{1}} + \frac{CC_{1}}{FC_{1}}$ $\frac{AA_{1}}{DA_{1}} + \frac{BB_{1}}{EB_{1}} + \frac{CC_{1}}{FC_{1}}$ đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó.

b) $\frac{AA_{1}}{AD} + \frac{BB_{1}}{BE} + \frac{CC_{1}}{CF}$ $\frac{AA_{1}}{AD} + \frac{BB_{1}}{BE} + \frac{CC_{1}}{CF}$ đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó.

Bài 4. Cho tam giác $ABC$ và $M$ là điểm nằm trong tam giác. Kẻ $AM,BM,CM$ cắt các cạnh $BC,CA,AB$ lần lượt tại $A_{1},B_{1},C_{1}$ $A_{1},B_{1},C_{1}$. Xác định vị trí của điểm $M$ để: $\frac{MA}{MA_{1}}.\frac{MB}{MB_{1}}.\frac{MC}{MC_{1}}$ $\frac{MA}{MA_{1}}.\frac{MB}{MB_{1}}.\frac{MC}{MC_{1}}$ đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

---------------------------------------------

Trên đây là tổng hợp kiến thức và phương pháp giải các bài toán tìm giá trị lớn nhất, nhỏ nhất của biểu thức hình học thường gặp trong chương trình THCS. Để nắm chắc dạng bài này, bạn hãy luyện tập thêm nhiều bài tập tự luyện, kết hợp với việc nắm vững các bất đẳng thức và kỹ thuật biến đổi hình học. Chúc bạn học tốt và đạt kết quả cao trong các kỳ thi sắp tới!

Tải về

Chọn file muốn tải về: