VnDoc.com

Viết phương trình đường thẳng thỏa mãn điều kiện cho trước

Chuyên đề Toán 9 luyện thi vào lớp 10

Bài trước

Tải về

Bài sau

Chuyên đề thi vào 10: Viết phương trình đường thẳng

I. Kiến thức cơ bản cần nhớ khi viết phương trình đường thẳng
II. Bài tập ví dụ về viết phương trình đường thẳng thỏa mãn điều kiện cho trước
III. Bài tập tự luyện về viết phương trình đường thẳng thỏa mãn điều kiện cho trước

Viết phương trình đường thẳng thỏa mãn điều kiện cho trước cung cấp kiến thức cơ bản cần nhớ khi viết phương trình đường thẳng; các bài tập ví dụ về viết phương trình đường thẳng thỏa mãn điều kiện cho trước.... giúp các em nắm vững các dạng bài tập ôn thi vào lớp 10 môn Toán.

I. Kiến thức cơ bản cần nhớ khi viết phương trình đường thẳng

1. Xác định hàm số y = ax + b biết hệ số góc a và đồ thị của nó đi qua điểm A(m; n)

+ Thay hệ số góc vào hàm số

+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta sẽ tìm được b

2. Đồ thị của hàm số y = ax + b song song với đường thẳng y = a’x + b’ và đi qua A(m; n)

+ Đồ thị hàm số y = ax + b song song với đường thẳng y = a’x + b’ nên a = a’

+ Thay a = a’ vào hàm số

+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta sẽ tìm được b

3. Đồ thị của hàm số y = ax + b vuông góc với đường thẳng y = a’x + b’ và đi qua A(m; n)

+ Đồ thị hàm số y = ax + b vuông góc với đường thẳng y = a’x + b’ nên a.a’ = -1 sau đó thay a vừa tìm được vào hàm số

+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta sẽ tìm được b

4. Đồ thị của hàm số y = ax + b đi qua hai điểm A(m; n) và B(p; q)

+ Vì đồ thị của nó đi qua A(m; n) nên thay x = m và y = n vào hàm số ta được phương trình thứ nhất

+ Vì đồ thị của nó đi qua B(p; q) nên thay x = p và y = q vào hàm số ta được phương trình thứ hai

+ Giải hệ phương trình gồm hai phương trình trên ta sẽ tìm được a và b

5. Đồ thị của hàm số y = ax + b đi qua A(m; n) và cắt trục hoành tại điểm có hoành độ bằng c

+ Đồ thị hàm số y = ax + b cắt trục hoành tại điểm có hoành độ bằng c nên nó đi qua điểm B(0; c)

+ Bài toán trở thành viết phương trình đường thẳng biết đồ thị hàm số đi qua hai điểm A(m; n) và B(0; c)

6. Đồ thị của hàm số y = ax + b đi qua A(m; n) và cắt trục tung tại điểm có tung độ bằng c

+ Đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng c nên nó đi qua điểm B(c; 0)

+ Bài toán trở thành viết phương trình đường thẳng biết đồ thị hàm số đi qua hai điểm A(m; n) và B(c; )

II. Bài tập ví dụ về viết phương trình đường thẳng thỏa mãn điều kiện cho trước

Ví dụ 1: Viết phương trình đường thẳng (d) của hàm số y = ax + b biết:

a, Hàm số có hệ số góc là 2 và đường thẳng (d) đi qua điểm A(1; -1)

b, Đường thẳng (d) song song với đường thẳng y = x + 1 và đi qua điểm A(1; 2)

c, Đường thẳng (d) vuông góc với đường thẳng y = 3x + 2 và đi qua điểm A(-1; -1)

d, Đường thẳng (d) đi qua hai điểm A(1; 1) và B(3; -2)

e, Đường thẳng (d) đi qua điểm A(3; 1) và cắt trục hoành tại điểm có hoành độ bằng -2

f, Đường thẳng (d) đi qua điểm A(1; 1) và cắt trục tung tại điểm có tung độ bằng 3

Lời giải:

a, Đồ thị hàm số y = ax + b có hệ số góc là 2 nên a = 2. Khi đó đồ thị hàm số có dạng y = 2x + b

Đường thẳng (d) có hàm số y = 2x + b đi qua điểm A(1; 1) nên khi thay tọa độ điểm A vào phương trình đường thẳng ta được:

1 = 2 + b hay b = -1

Vậy phương trình đường thẳng (d) cần tìm là: y = 2x – 1

b, Đường thẳng (d) song song với đường thẳng y = x + 1 nên phương trình của đường thẳng (d) có dạng y = x + b

Đường thẳng (d) đi qua điểm A(1;2) nên khi thay tọa độ điểm A vào phương trình đường thẳng ta được:

2 = 1 + b hay b = 1

Vậy phương trình đường thẳng (d) cần tìm là: y = x + 1

c, Đường thẳng (d) vuông góc với đường thẳng y = 3x + 2 nên phương trình của đường thẳng (d) có dạng $y = \frac{{ - 1}}{3}x + b$ $y = \frac{- 1}{3} x + b$

Đường thẳng (d) đi qua điểm A(-1; -1) nên khi thay tọa độ điểm A vào phương trình đường thẳng ta được: $- 1 = \frac{1}{3} + b \Leftrightarrow b = \frac{{ - 4}}{3}$ $- 1 = \frac{1}{3} + b \Leftrightarrow b = \frac{- 4}{3}$

Vậy phương trình đường thẳng (d) cần tìm là: $y = \frac{{ - 1}}{3}x - \frac{4}{3}$ $y = \frac{- 1}{3} x - \frac{4}{3}$

d, Gọi phương trình đường thẳng (d) có dạng y = ax + b

Đường thẳng (d) đi qua điểm A(1; 1) nên khi thay tọa độ điểm A vào phương trình đường thẳng ta được phương trình a + b = 1 (1)

Đường thẳng (d) đi qua điểm B(3; -2) nên khi thay tọa độ điểm B vào phương trình đường thẳng ta được phương trình 3a + b = -2 (2)

Từ (1) và (2) ta giải ra được $a = \frac{{ - 3}}{2};b = \frac{5}{2}$ $a = \frac{- 3}{2}; b = \frac{5}{2}$

Vậy phương trình đường thẳng (d) cần tìm là: $y = \frac{{ - 3}}{2}x + \frac{5}{2}$ $y = \frac{- 3}{2} x + \frac{5}{2}$

e, Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng -2 nên đường thẳng (d) đi qua điểm B(-2; 0)

Gọi phương trình đường thẳng (d) có dạng y = ax + b

Đường thẳng (d) đi qua điểm A(3; 1) nên khi thay tọa độ điểm A vào phương trình đường thẳng ta được phương trình 3a + b = 1 (1)

Đường thẳng (d) đi qua điểm B(-2; 0) nên khi thay tọa độ điểm B vào phương trình đường thẳng ta được phương trình -2a + b = 0 (2)

Từ (1) và (2) ta giải ra được

Vậy phương trình đường thẳng (d) cần tìm là:

f, Đường thẳng (d) cắt trục hoành tại điểm có tung độ bằng 3 nên đường thẳng (d) đi qua điểm B(0; 3)

Gọi phương trình đường thẳng (d) có dạng y = ax + b

Đường thẳng (d) đi qua điểm A(1; 1) nên khi thay tọa độ điểm A vào phương trình đường thẳng ta được phương trình a + b = 1 (1)

Đường thẳng (d) đi qua điểm B(0; 3) nên khi thay tọa độ điểm B vào phương trình đường thẳng ta được phương trình b = 3 (2)

Từ (1) và (2) ta giải ra được a = -2 và b = 3

Vậy phương trình đường thẳng (d) cần tìm là: y = -2x + 3

Ví dụ 2. Viết phương trình đường thẳng biết:

a. Đường thẳng đi qua hai điểm $A (1, 2), B (3, - 1)$

b. Đường thẳng đi qua điểm $A (- 1, 3)$ và song song với đường thẳng $3 x - 4 y - 1 = 0$

c. Đường thẳng đi qua $A (2, 3)$ và vuông góc với đường thẳng $2 x + y + 3 = 0$

Hướng dẫn giải

Giả sử đường thẳng có dạng y = ax + b

a. Đường thẳng đi qua điểm $A (1, 2), B (3, - 1)$ ta có hệ phương trình:

$\left\{ \begin{matrix} a + b = 2 \\ 3a + b = - 1 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} a = \dfrac{- 3}{2} \\ b = \dfrac{7}{2} \\ \end{matrix} \right.\ \Rightarrow y = \dfrac{- 3}{2}x + \frac{7}{2}$ ${\begin{matrix} a + b = 2 \\ 3 a + b = - 1 \end{matrix} \Leftrightarrow {\begin{matrix} a = \frac{- 3}{2} \\ b = \frac{7}{2} \end{matrix} \Rightarrow y = \frac{- 3}{2} x + \frac{7}{2}$

b. Đường thẳng đi qua điểm $A( - 1,3) \Leftrightarrow - a + b = 3$ $A (- 1, 3) \Leftrightarrow - a + b = 3$ (1)

Đường thẳng song song với đường thẳng $3x - 4y - 1 = 0 \Leftrightarrow y = \frac{3}{4}x - \frac{1}{4}$ $3 x - 4 y - 1 = 0 \Leftrightarrow y = \frac{3}{4} x - \frac{1}{4}$

$\Rightarrow a = \frac{3}{4}$ $\Rightarrow a = \frac{3}{4}$ (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{ \begin{matrix} - a + b = 3 \\ a = \frac{3}{4} \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} a = \frac{3}{4} \\ b = \frac{15}{4} \\ \end{matrix} \right.\ \right.\ \Rightarrow y = \frac{3}{4}x + \frac{15}{4}$ ${\begin{matrix} - a + b = 3 \\ a = \frac{3}{4} \end{matrix} \Leftrightarrow {\begin{matrix} a = \frac{3}{4} \\ b = \frac{15}{4} \end{matrix} \Rightarrow y = \frac{3}{4} x + \frac{15}{4}$

c. Đường thẳng đi qua $A(2,3) \Rightarrow 2a + b = 3$ $A (2, 3) \Rightarrow 2 a + b = 3$ (1)

Đường thẳng vuông góc với đường thẳng $- 2 x - 3 = y$

$\Rightarrow a.( - 2) = - 1 \Rightarrow a = \frac{1}{2}$ $\Rightarrow a . (- 2) = - 1 \Rightarrow a = \frac{1}{2}$ (2)

Từ (1) và (2) ta có: $\left\{ \begin{matrix} 2a + b = 3 \\ a = \frac{1}{2} \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} a = \frac{1}{2} \\ b = 2 \\ \end{matrix} \right.\ \right.\ \Rightarrow y = \frac{1}{2}x + 2$ ${\begin{matrix} 2 a + b = 3 \\ a = \frac{1}{2} \end{matrix} \Leftrightarrow {\begin{matrix} a = \frac{1}{2} \\ b = 2 \end{matrix} \Rightarrow y = \frac{1}{2} x + 2$

Ví dụ 3. Đồ thị của một hàm số bậc nhất đi qua điểm $C (0; 5)$ và song song với đường thẳng $x - 4 y = 10$ . Xác định hàm số bậc nhất đó?

Hướng dẫn giải:

Ta có: $x - 4y = 10 \Rightarrow y = \frac{x}{4} - \frac{5}{2}$ $x - 4 y = 10 \Rightarrow y = \frac{x}{4} - \frac{5}{2}$

Hàm số bậc nhất cần tìm có dạng $y = ax + b;(a \neq 0)(*)$ $y = a x + b; (a \neq 0) (*)$

Đồ thị hàm số $(*)$ song song với đồ thị hàm số $y = \frac{x}{4} - \frac{5}{2}$ $y = \frac{x}{4} - \frac{5}{2}$ khi đó: $a = \frac{1}{4}$ $a = \frac{1}{4}$

$\Rightarrow y = \frac{1}{4}x + b;(**)$ $\Rightarrow y = \frac{1}{4} x + b; (* *)$

Đồ thị hàm số (*) đi qua điểm $C (0; 5)$ nên

$\Rightarrow 5 = \frac{1}{4}.0 + b \Rightarrow b = 5$ $\Rightarrow 5 = \frac{1}{4} .0 + b \Rightarrow b = 5$

Vậy hàm số cần tìm là $y = \frac{1}{4}x + 5$ $y = \frac{1}{4} x + 5$

Ví dụ 4. Gọi A là giao điểm của hai đồ thị hai hàm số $y = 2 x + 2$ và $y = 2 x$ . Qua điểm $(0; 2)$ vẽ đường thẳng song song với trục hoành, cắt hai đường thẳng tại hai điểm B, C. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Hình vẽ minh họa

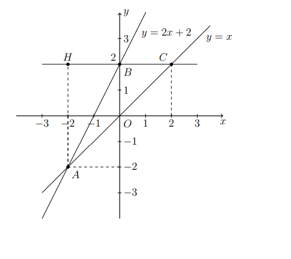
Dựa vào đồ thị ta có giao điểm A có tọa độ $A (- 2; 2)$

Qua điểm $(0; 2)$ vẽ đường thẳng song song với trục hoành, cắt hai đường thẳng tại hai điểm $B; C$ .

Tọa độ hai giao điểm $B (0; 2); C (2; 2)$ . Độ dài BC là 2

Kẻ $AH\bot BC$ $A H ⊥ B C$ khi đó ta có: $A H = 4$

Diện tích tam giác $A B C$ là: $S_{ABC} = \frac{1}{2}.AH.BC = \frac{1}{2}.2.4 = 4(dvdt)$ $S_{A B C} = \frac{1}{2} . A H . B C = \frac{1}{2} .2 .4 = 4 (d v d t)$

III. Bài tập tự luyện về viết phương trình đường thẳng thỏa mãn điều kiện cho trước

Bài 1: Viết phương trình đường thẳng y = ax + b biết đường thẳng đi qua hai đi qua hai điểm A(4; 3) và B(2; -1)

Bài 2: Viết phương trình đường thẳng d đi qua điểm M(-2; 0) và cắt trục tung tại điểm có tung độ là 3

Bài 3: Viết phương trình đường thẳng (d) song song với đường thẳng y = 3x + 1 và cắt trục tung tại hai điểm có tung độ là 4

Bài 4: Viết phương trình đường thẳng (d) song song với đường thẳng (d’): y = -2x và đi qua điểm A(2; 7)

Bài 5: Viết phương trình đường thẳng (d) có hệ số góc là -1 và đi qua gốc tọa độ

Bài 6: Hãy xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:

a, Có hệ số góc là 3 và đi qua điểm A(1; 0)

b, Song song với đường thẳng y = x – 2 và cắt trục tung có tung độ bằng 2

Bài 7: Viết phương trình đường thẳng (d) đi qua điểm M(1; -2) và song song với đường thẳng (d’): x + 2y = 1

Bài 8: Viết phương trình đường thẳng (d) cắt đường thẳng (d’): x – y + 1 = 0 tại điểm có tung độ bằng 2 và vuông góc với đường thẳng (d”): y = 3 – x

Bài 9: Viết phương trình đường thẳng (d) đi qua gốc tọa độ và đi qua giao điểm của hai đường thẳng (d’): y = 4x – 3 và (d”): y = -x + 3

Bài 10: Viết phương trình trình đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 5 và đi qua điểm M(2; 3).

Bài 11. a. Viết phương trình đường thẳng đi qua hai điểm $A (- 10, 2), B (4, 2)$

b. Viết phương trình đường thẳng có hệ số góc a = 3 và đi qua điểm $B (1, - 1)$

c. Viết phương trình đường thẳng đi qua điểm $A (- 1, 2)$ song song với đường thẳng $y = 2 x - 1$

d. Viết phương trình đường thẳng đi qua điểm $M (3, 2)$ và vuông góc với đường thẳng $y = - x + 2$

--------------------------------

Mời bạn đọc tải tài liệu tham khảo đầy đủ của chúng tôi!

Chia sẻ, đánh giá bài viết

10

43.977

Bài trước

Bài sau

Chia sẻ bởi:
Lê Hằng Anh

Tải về

Chọn file muốn tải về:

Viết phương trình đường thẳng thỏa mãn điều kiện cho trước

292,5 KB

Tải tài liệu định dạng .doc
126 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

Gợi ý cho bạn

Xem thêm

Đề thi vào 10 môn Toán

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Giáo án STEAM

Dạy con học

Giáo án

Trường mầm non

Danh mục Trường Tiểu học

Sáng kiến kinh nghiệm

Thư viện Đề thi

Bài tập cuối tuần

Trắc nghiệm

Sách Cánh diều

Sách Chân trời sáng tạo

Sách Kết nối tri thức

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 2

Môn Tiếng Việt lớp 2

Chuyên đề - Văn mẫu

Môn Tiếng Anh

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 3

Môn Tiếng Việt lớp 3

Chuyên đề - Văn mẫu

Tiếng Anh lớp 3

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 4

Môn Tiếng Việt lớp 4

Tiếng Anh lớp 4

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 5

Môn Tiếng Việt lớp 5

Môn Tiếng Anh 5

Thi vào lớp 6

Tài liệu Giáo viên

Ôn thi

Thư Viện Đề Thi

Trắc nghiệm

Khóa Học Trực Tuyến

Môn Toán