Các dạng bất đẳng thức trong đường tròn thường gặp

Bất đẳng thức trong đường tròn Toán 9 

Bất đẳng thức trong đường tròn là một chuyên đề quan trọng trong chương trình Toán học THCS, đặc biệt thường xuyên xuất hiện trong các đề thi học kỳ, đề thi học sinh giỏi và kỳ thi tuyển sinh vào lớp 10. Bài viết này sẽ hệ thống lại các dạng bất đẳng thức trong đường tròn thường gặp, cung cấp phương pháp giải cụ thể, ví dụ minh họa có lời giải chi tiết, giúp học sinh hiểu bản chất và rèn luyện tư duy giải bài hiệu quả. Cùng khám phá ngay!

A. Kiến thức cần nhớ

B. Bài tập minh họa bất đẳng thức đường tròn

Bài 1: Cho đường tròn \((O;R)\) và điểm \(A\) nằm ngoài đường tròn đó. Một đường thẳng \(\Delta\) thay đổi quanh \(A\) cắt \((O;R)\) tại hai điểm \(M,N\). Tìm vị trí \(\Delta\) để \(AM + AN\) lớn nhất.

Hướng dẫn giải:

Hình vẽ minh họa

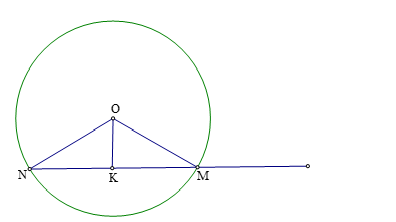
Gọi \(K\) là trung điểm của dây cung

\(MN\) ta có:

\(AM + AN = AM + (AM + MN)\)

\(= 2AM + 2MK = 2AK\)

Xét tam giác vuông \(OKA\)

Ta có: \(OK^{2} + KA^{2} = OA^{2}\) không đổi.

Như vậy \(AK\) lớn nhất khi và chỉ khi \(OK\) nhỏ nhất \(\Leftrightarrow OK = 0 \Leftrightarrow A,M,N,O\) nhỏ nhất.

Bài 2: Cho đường tròn \((O;R)\) và dây cung \(AB\) cố định \((AB < 2R)\). Trên cung lớn \(AB\) lấy điểm \(M\). Tìm vị trí điểm \(M\) để chu vi tam giác \(MAB\) lớn nhất

Hướng dẫn giải:

Hình vẽ minh họa

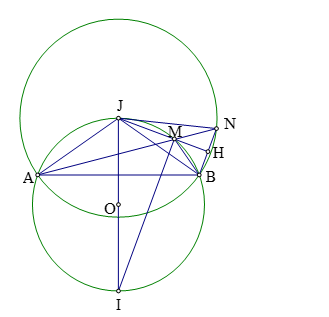
Trên tia đối của \(AM\) lấy điểm \(N\) sao cho \(MN = MB\).

Khi đó chu vi tam giác \(MAB\) là \(2p = MA + MB + AB = AN + AB\).

Do \(AB\) không đổi nên chu vi tam giác \(MAB\) lớn nhất khi và chỉ khi \(AN\) lớn nhất.

Tam giác \(BMN\) cân tại \(M\) và \(MH\)là phân giác của góc \(\widehat{BMN}\) đồng thời cũng là phân giác ngoài của góc \(\widehat{AMB}\).

Phân giác trong của góc \(\widehat{AMB}\) là \(MI\) với \(I\) là trung điểm cung lớn \(AB\). Suy ra \(MI\bot MH\).

Do đó \(MH\) cắt đường tròn \((O;R)\)tại điểm \(J\) và \(IJ\) là đường kính của \((O;R)\).

Tam giác \(MBN\) cân tại \(M\) nên \(MJ\) là đường trung trực của \(BN\).

Từ đó ta có: \(JA = JB = JN\).

Hay điểm \(N\) thuộc đường tròn tâm \(J\) cố định bán kính \(JA\).

Vì \(AN\) là dây cung của đường tròn \((J)\) nên \(AN\) lớn nhất khi và chỉ khi \(AN\) là đường kính của \((J) \Leftrightarrow M \equiv J\).

Như vậy chu vi tam giác \(MAB\) lớn nhất khi và chỉ khi \(M\) trùng với trung điểm \(J\) của cung nhỏ \(AB\).

Bài 3: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB < AC\) ngoại tiếp đường tròn tâm \(O\). Gọi \(D,E,F\) lần lượt là tiếp điểm của \((O)\) với các cạnh \(AB,AC,BC\); \(M\) là điểm di chuyển trên đoạn \(CE\). Gọi \(N\) là giao điểm của \(BM\) với cung nhỏ \(EF\) của \((O)\), \(P\) và \(Q\) lần lượt là hình chiếu của \(N\) trên các đường thẳng \(DE,DF\). Xác định vị trí của điểm \(M\) để \(PQ\) lớn nhất

Hướng dẫn giải:

Hình vẽ minh họa

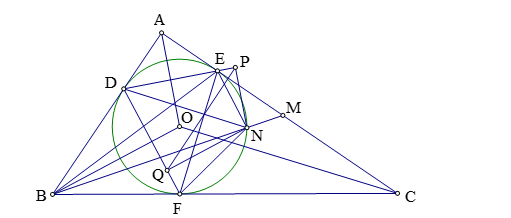
Ta có tứ giác \(PNQD\) , \(EDFN\) nội tiếp \(\Rightarrow \widehat{QPN} = \widehat{QDN} = \widehat{FEN}\).

Tương tự có ta có: \(\widehat{NQP} = \widehat{NDP} = \widehat{NFE}\) \(\Rightarrow \Delta NEF\sim\Delta NPQ\). Suy ra \(\frac{PQ}{EF} = \frac{NQ}{NF}\).

Trong tam giác vuông \(NQF\) ta có: \(NQ \leq NF\) do đó \(\frac{PQ}{EF} \leq 1\).

Như vậy \(PQ\) lớn nhất bằng \(EF\) khi và chỉ khi \(Q \equiv F\) khi đó \(P \equiv E\), do \(P\) và \(Q\) lần lượt là hình chiếu của \(N\) trên các đường thẳng \(DE,DF\) nên khi \(Q \equiv F\) , \(P \equiv E\) thì \(DN\) là đường kính của \((O)\).

Từ đó suy ra cách xác định \(M\) như sau: Dựng đường kính \(DN\) của \((O)\), \(M\) là giao điểm của \(BN\) và \(AC\).

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

----------------------------------------

Trên đây là toàn bộ các dạng bất đẳng thức trong đường tròn thường gặp kèm theo phương pháp giải và ví dụ cụ thể. Hy vọng nội dung này sẽ giúp bạn củng cố kiến thức và tự tin hơn khi làm bài thi. Hãy thường xuyên luyện tập để thành thạo các kỹ thuật giải nhanh và nâng cao năng lực tư duy hình học của bản thân. Đừng quên lưu lại bài viết và chia sẻ cho bạn bè nếu bạn thấy hữu ích nhé!