Đề cương ôn tập cuối học kì 2 Toán 9 trường THCS Vạn Yên, Hà Nội năm 2024 - 2025
Đề cương Toán 9 học kì 2
Lớp:
Lớp 9
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
1
TRƯỜNG THCS VẠN YÊN
HƯỚNG DẪN ÔN TẬP CUỐI HỌC KÌ II
Năm học 2024-2025
MÔN TOÁN 9
I. ĐẠI SỐ
Dạng 1. Xác suất và thống kê
Bài 1.
1) Ban phụ huynh đặt tặng áo phông cho 40 học sinh của lớp 9A. Ban phụ huynh đo chiều cao
(đơn vị: centimét) của cả lớp để quyết định chọn các cỡ áo, kết quả cho bởi bảng tần số ghép
nhóm như sau:
Nhóm
150;155
155;160
160; 165
165; 170
170; 175
Cộng
Tần số
(n)
5
11
12
8
4
N = 40
Xác định tần số ghép nhóm và tìm tần số tương đối ghép nhóm của nhóm
160; 165
.
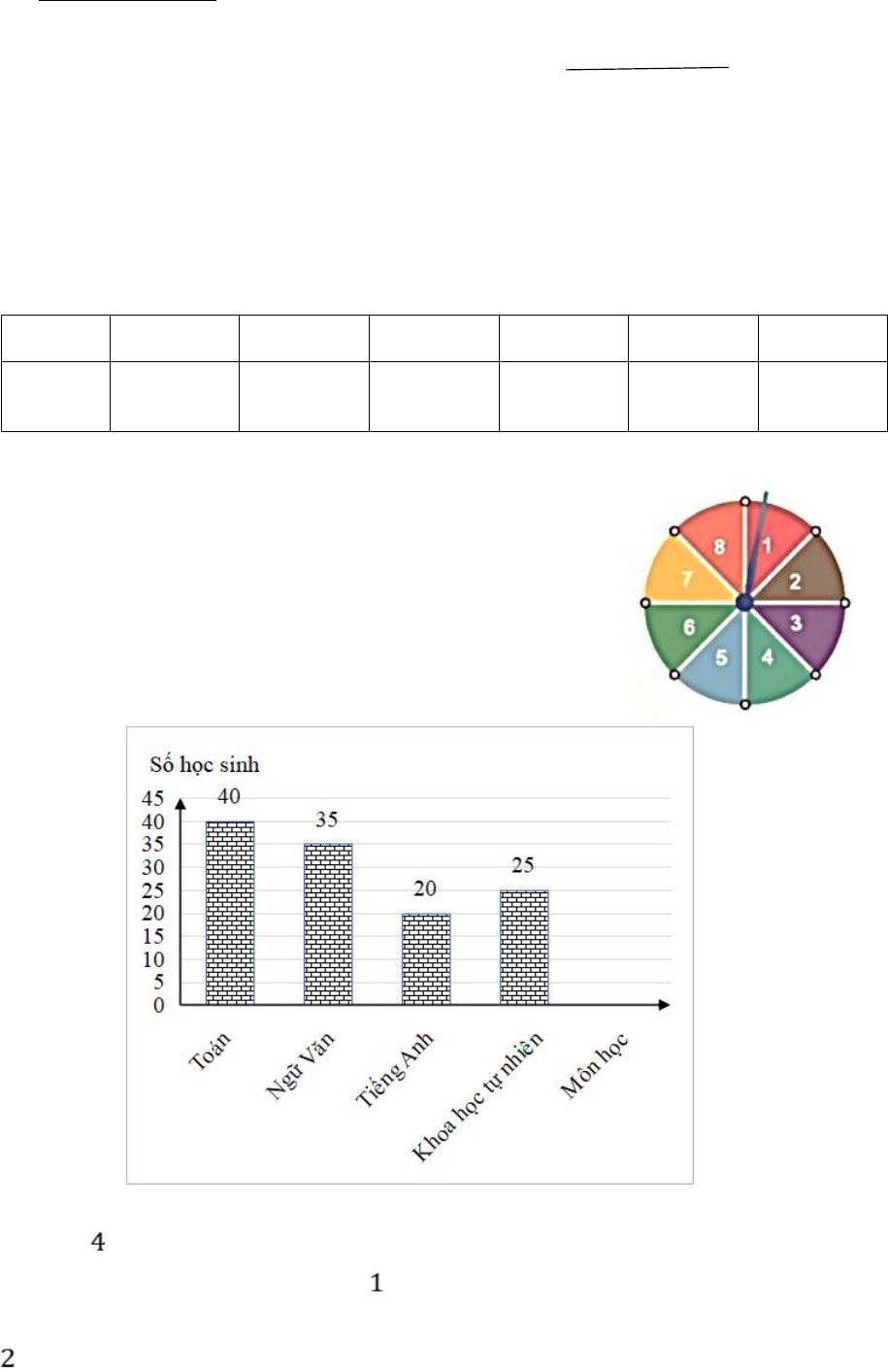
2) Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám
phần bằng nhau và ghi các số
1; 2; 3; ; 8
. Chiếc kim được gắn cố
định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác
suất của biến cố A: “Chiếc kim chỉ vào hình quạt ghi số lớn hơn 3”.
Bài 2.
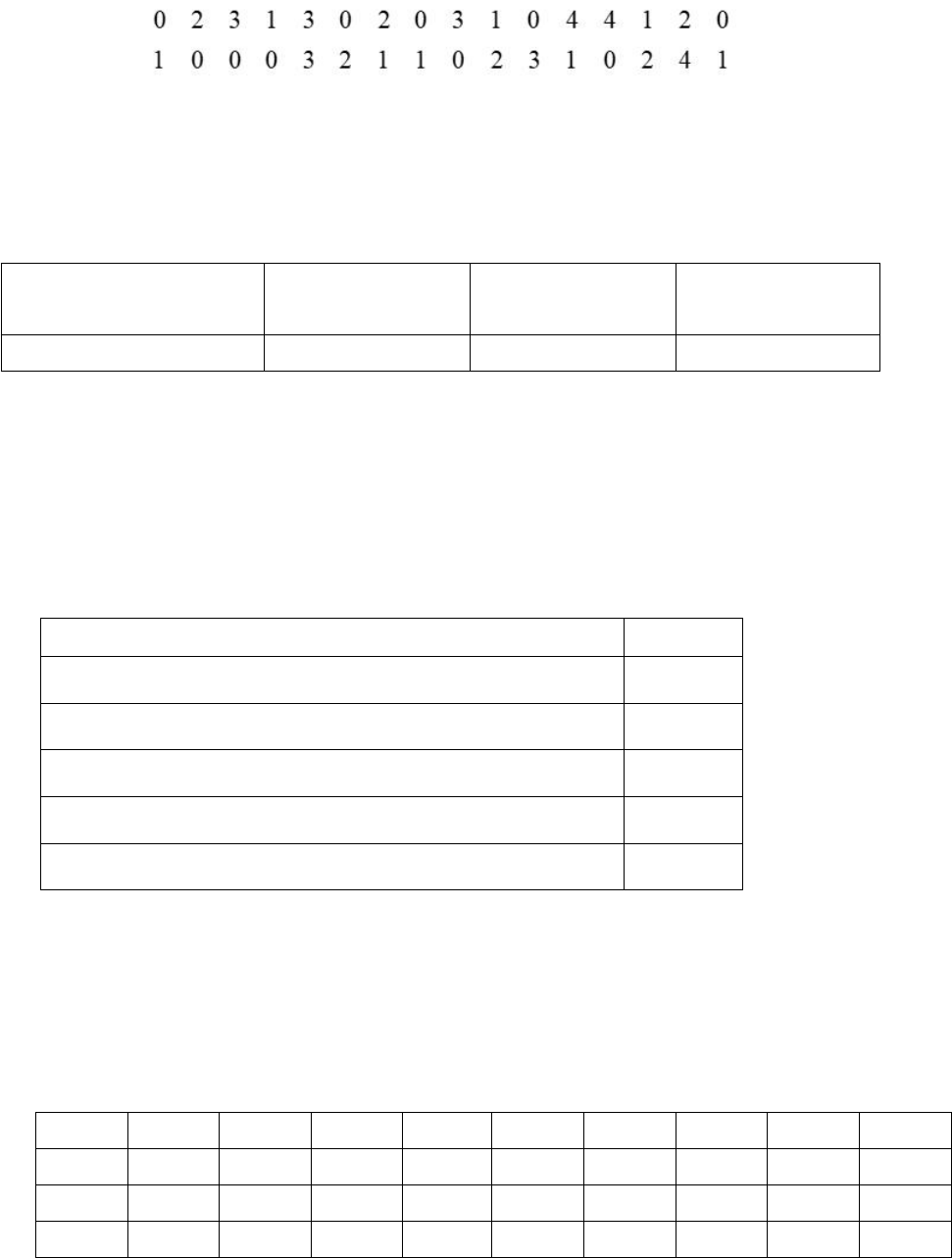
1) Biểu đồ hình cột sau thống kê về sự yêu thích các môn học của
học sinh khối
9
. Biết mỗi học sinh chỉ chọn một môn yêu thích.
Lập bảng tần số và bảng tần số tương đối của dữ liệu được biểu diễn trên biểu đồ.
2) Một hộp chứa tấm thẻ cùng loại. Trên mỗi tấm thẻ được đánh số tương ứng là 2; 3; 5; 8. Bạn
Phi và bạn Thanh lần lượt mỗi người lấy ra tấm thẻ từ hộp (Biết trong mỗi đợt lấy thì bạn Phi
lấy tấm thẻ trước và không bỏ tấm thẻ lại vào hộp). Tính xác suất của biến cố sau: M “Tích các số
ghi trên tấm thẻ là số lẻ”.
2
Bài 3.
1) Sau bài kiểm tra môn Ngữ văn, giáo viên ghi lại số lỗi trong bài làm của 32 học sinh mắc phải
như sau:
a) Tính tần số tương đối của số lỗi chính tả mà 32 học sinh mắc phải.
b) Trong số học sinh được khảo sát, giáo viên muốn chọn ra 25% số học sinh mắc nhiều lỗi nhất
để hướng dẫn cách sửa. Hỏi giáo viên cần chọn các học sinh mắc bao nhiêu lỗi?
2) Một nhà máy sản xuất linh kiện điện tử, kiểm tra chất lượng 100 sản phẩm. Kết quả kiểm tra
được ghi trong bảng sau:
Số
lỗi
0
1
> 1
Số sản phẩm
62
35
3
Chọn ngẫu nhiên một sản phẩm của nhà máy. Hãy tính xác suất của các biến cố sau:
A: “Sản phẩm không có lỗi”.
B: “Sản phẩm có đúng 1 lỗi”.
C: “Sản phẩm có nhiều hơn 1 lỗi”.
Bài 4.
1) Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của
40
học sinh trong lớp
thành 5 nhóm (đơn vị: phút) và lập bảng tần số ghép nhóm như sau:
Thời gian sử dụng Internet trong một ngày (phút)
Tần số
0;60
6
60;120
13
120;180
13
180;240
6
240;300
2
Tìm tần số ghép nhóm và tần số tương đối ghép nhóm của nhóm
180;240
2) Có hai túi I và II, mỗi túi chứa 4 tấm thẻ được đánh số 1, 2, 3, 4. Rút ngẫu nhiên từ mỗi túi ra
một tấm thẻ và nhân hai số ghi trên tấm thẻ với nhau. Tính xác suất của biến cố A “Kết quả là
một hoặc một số nguyên tố”
Bài 5.
1) Điểm đánh giá học kì I môn Toán của lớp 9A được người ta ghi lại bảng như sau:
8,5
8
8
7,5
9
8,5
7
9
8
8
6,5
9,3
8,5
8,5
6
9
7,5
8,5
8,5
8
8
6
9,3
6,5
8
5,5
5
8
8
8,5
8,5
7,5
8,5
7,5
8
8,5
9
8
8,5
9
Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu trên với các
nhóm
5;6,5 ; 6,5;8 ; 8;9,5
.
2) Lấy ngẫu nhiên một thẻ từ một hộp chứa 20 thẻ được đánh số từ 1 đến 20. Tìm xác suất để thẻ
được lấy ghi số lẻ và chia hết cho 5
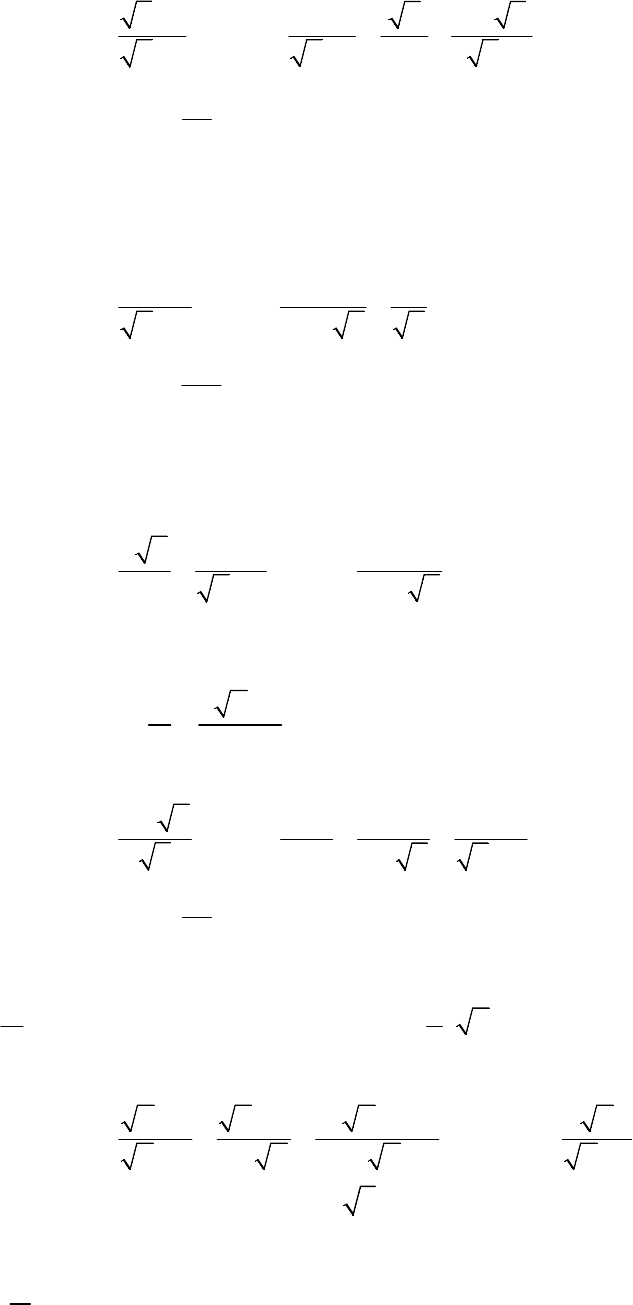
3
Dạng 2. Bài toán rút gọn và các câu hỏi có liên quan
Bài 1.
Cho hai biểu thức
1
1
x
A
x
và
1
.
1
1 2 1
x x x
B
x
x x
với
0, 1 x x
.
a) Tính giá trị của A khi
16
x
25
.
b) Rút gọn biểu thức B.
c) Với
, 1 x x
. Hãy tìm giá trị lớn nhất của biểu thức P = AB.
Bài 2.
Cho hai biểu thức
1
2
A
x
và
2 1
2
x
B
x x x
với x > 0.
a) Tính giá trị của A khi
1
x
100
.
b) Đặt P = A + B. Hãy rút gọn P.
c) So sánh P với 1.
Bài 3.
Cho hai biểu thức
2 2
9
3
x
A
x
x
và
3
3
B
x x
với
0, 9 x x
.
a) Tính giá trị của A khi x = 100.
b) Rút gọn biểu thức A.
c) Tìm giá trị của x, biết:
B 2 x 1
A 2
.
Bài 4.
Cho hai biểu thức
2
x
A
x
và
1 1
4
2 2
x
B
x
x x
với
0, 4 x x
.
a) Tính giá trị của A khi
4
x
25
.
b) Rút gọn biểu thức B.
c) Cho
A
P
B
. Tìm giá trị nguyên của x, biết:
3
P.x x 1
2
.
Bài 5.
Cho các biểu thức
x 3 x 2 x 2
P
x 2 3 x x 5 x 6
và
x
Q 1
x 1
với
x 0; x 4; x 9
.
a) Tính giá trị của biểu thức Q khi
x 4 2 3
.
b) Rút gọn biểu thức
T P : Q
.
c) Tìm x để
1
T
có giá trị nguyên.
Đề cương ôn thi cuối học kì 2 Toán 9 năm 2025
Đề cương ôn tập cuối học kì 2 Toán 9 trường THCS Vạn Yên, Hà Nội năm 2024 - 2025 gồm tóm tắt lý thuyết trọng tâm kèm bài tập minh họa, thầy cô có thể tham khảo ra đề và ôn luyện cho học sinh. Đây cũng là tài liệu hay cho các em học sinh ôn tập, chuẩn bị cho kì thi sắp tới.
Ngoài tài liệu trên, mời các bạn tham khảo thêm các đề thi học kì 2 lớp 9 trên VnDoc với đầy đủ các môn. Đây là tài liệu hay giúp các em làm quen với nhiều dạng đề thi khác nhau, nắm được cấu trúc đề thi, từ đó đạt điểm cao trong các kì thi quan trọng.




