Đề thi học kì 2 Toán 9 Sở GD&ĐT Đồng Nai năm 2024 - 2025
Đề thi hk2 Toán 9 có đáp án
Tìm hiểu thêm
Tặng thêm 15 ngày khi mua gói 4 tháng.
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA CUỐI HỌC KỲ II LỚP 9
TỈNH ĐỒNG NAI NĂM HỌC 2024-2025
ĐỀ CHÍNH THỨC Môn: Toán học
Thời gian làm bài: 90 phút
Ngày kiểm tra: 24/4/2025
(Đề kiểm tra gồm một trang, có năm bài tự luận)
Bài 1. (1,5 điểm)
1) Giải phương trình x
2
− 8x + 7 = 0.
2) Vẽ đồ thị hàm số y = x
2
.
Bài 2. (3,5 điểm)
1) Chứng minh phương trình x
2
−7x + 1 = 0 có hai nghiệm phân biệt x
1
, x
2
và tính giá trị của biểu
thức M = x
1
+ x
2
− x
1
x
2
(không giải phương trình).
2) Tìm hai số biết tổng của chúng bằng 3 và tích của chúng bằng −10.
3) Cô An trồng một vụ rau trên một thửa đất hình chữ nhật có chiều dài hơn chiều rộng 14 m. Khi
thu hoạch, cô An bán rau được bình quân 10 (nghìn đồng) trên mỗi mét vuông đất. Tính chiều rộng và
chiều dài của thửa đất đó, biết tổng số tiền cô An bán rau thu hoạch từ thửa đất đó 950 (nghìn đồng).
Bài 3. (1 điểm)
1) Số các quyển sách của 36 học sinh lớp 9A tặng để “đồng hành cùng các bạn ở vùng khó khăn”,
được cô giáo ghi trong bảng phía dưới. Hãy lập bảng tần số của mẫu số liệu đó.
2) Câu lạc bộ “Yêu thích Toán học” của lớp 9A có 5 học sinh gồm 2 học sinh nam và 3 học sinh nữ.
Chọn ngẫu nhiên 1 học sinh của câu lạc bộ đó để giao lưu cấp trường. Tính xác suất của biến cố “1 học
sinh được chọn là học sinh nữ”.
Bài 4. (1 điểm)
1) Tính bán kính đường tròn nội tiếp tam giác đều có cạnh bằng 6 cm.
2) Tính thể tích một hộp sữa có dạng hình trụ với bán kính đáy 3, 8 cm và chiều cao 8 cm (kết quả
làm tròn đến hàng phần mười).
Bài 5. (3 điểm)
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có 3 đường cao AD, BE, CF cắt nhau tại điểm H.
1) Chứng minh tứ giác BCEF nội tiếp đường tròn.
2) Chứng minh
[
AEF =
[
ABC.
3) Gọi P, Q, R lần lượt là giao điểm của ba đường thẳng AD, BE, CF với (O) tương ứng khác A, B, C.
Chứng minh H là tâm của đường tròn nội tiếp tam giác P QR.
HẾT
Họ và tên thí sinh: ... . .. . ... ... . .. . .. . .Số báo danh: ..... Trường, trung tâm: .. . .. . .. . .. . ... ... . ..
Thí sinh được sử dụng máy tính cầm tay không có chức năng soạn thảo văn bản, không được sử dụng
tài liệu.
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
Bài
Ý
Nội dung
Điểm
1. 1,50
1)
Giải phương trình:
0,50
Ta có x
2
− 8x + 7 = 0.
Vì 1 + (−8) + 7 = 0
0,25
nên phương trình đã cho có hai nghiệm x
1
= 1, x
2
=
7
1
= 7.
0,25
Cách 2:
0,50
Ta có x
2
− 8x + 7 = 0
4
0
= (−4)
2
− 1.7 = 9 > 0
0,25
p
4
0
=
√
9 = 3.
Phương trình đã cho có hai nghiệm phân biệt là
x
1
=
−(−4) + 3
1
= 7, x
2
=
−(−4) − 3
1
= 1.
0,25
Cách 3:
0,50
Ta có x
2
− 8x + 7 = 0
4 = (−8)
2
− 4.1.7 = 36 > 0
0,25
Phương trình đã cho có hai nghiệm phân biệt là
x
1
=
−(−8) +
√
36
2.1
= 7, x
2
=
−(−8) −
√
36
2.1
= 1.
0,25
Cách 4:
0,50
Ta có x
2
− 8x + 7 = 0 ⇔ x
2
− x − 7x + 7 = 0 ⇔ x(x − 1) − 7(x − 1) = 0
⇔ (x −1)(x −7) = 0
0,25
⇔
"
x − 1 = 0
x − 7 = 0
⇔
"
x = 1
x = 7
· Vậy phương trình đã cho có tập nghiệm là {1 ; 7}.
0,25
Cách 5:
0,50
x
2
− 8x + 7 = 0
x
2
− x − 7x + 7 = 0
x(x − 1) − 7(x − 1) = 0
(x − 1)(x − 7) = 0
0,25
x − 1 = 0 hoặc x − 7 = 0
x = 1 hoặc x = 7
Vậy phương trình đã cho có các nghiệm x = 1, x = 7.
0,25
2)
Vẽ đồ thị hàm số:
1,00
y = x
2
Một số giá trị tương ứng của x và y:
x
y = x
2
−2 −1
0 1 2
4 1 0 1 4
0,25
Trên mặt phẳng tọa độ Oxy, lấy các điểm
(−2 ; 4), (−1 ; 1), (0 ; 0), (1 ; 1), (2 ; 4)
0,25
Trang 1
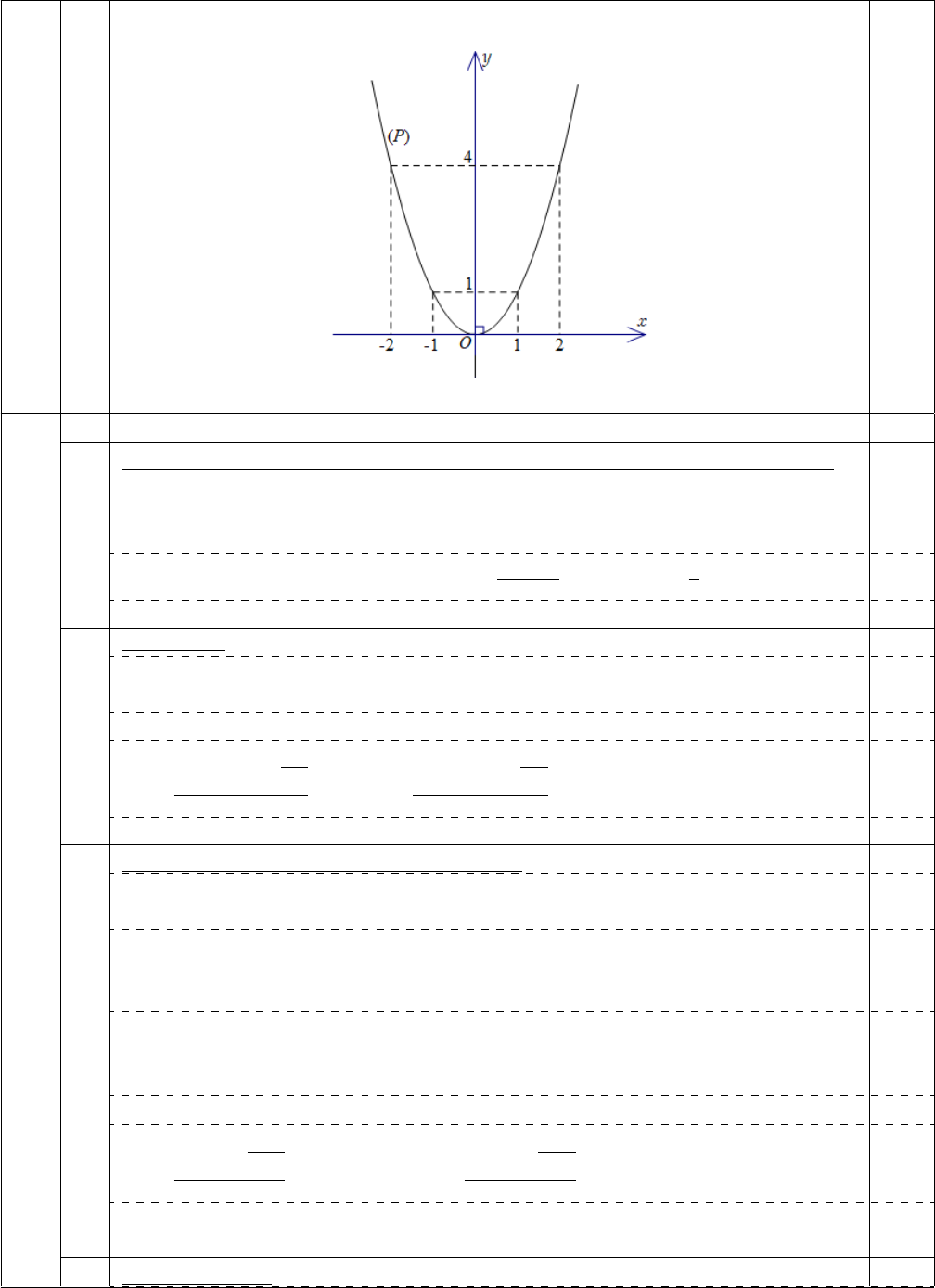
Vẽ đường parabol đi qua 5 điểm trên, được đồ thị (P ) của hàm số y = x
2
:
0,50
2. 3,50
1)
Chứng minh phương trình có hai nghiệm phân biệt và tính giá trị biểu thức:
1,00
Ta có x
2
− 7x + 1 = 0 (1)
4 = (−7)
2
− 4.1.1 = 45 > 0
nên phương trình (1) có hai nghiệm phân biệt x
1
, x
2
.
0,25
Áp dụng định lý Viète ta có x
1
+ x
2
=
−(−7)
1
= 7, x
1
x
2
=
1
1
= 1.
0,50
M = x
1
+ x
2
− x
1
x
2
= 7 − 1 = 6. 0,25
2)
Tìm hai số:
1,00
Hai số có tổng của chúng bằng 3 và tích của chúng bằng −10 là hai nghiệm
của phương trình x
2
− 3x − 10 = 0 (1).
0,25
4 = (−3)
2
− 4.1(−10) = 49 > 0 0,25
Phương trình (1) có hai nghiệm phân biệt là
x
1
=
−(−3) +
√
49
2.1
= 5, x
2
=
−(−3) −
√
49
2.1
= −2.
0,25
Hai số cần tìm là 5 và −2.
0,25
3)
Tính chiều rộng và chiều dài của thửa đất:
1,50
Gọi x (m) là chiều rộng của thửa đất hình chữ nhật đã cho. Điều kiện: x > 0.
Vì chiều dài hơn chiều rộng 14 m nên chiều dài của thửa đất x + 14 (m).
0,25
Diện tích thửa đất đó là x(x + 14) (m
2
).
Vì bình quân bán rau được 10 (nghìn đồng) trên mỗi mét vuông đất nên số
tiền bán rau thu hoạch từ thửa đất đó 10x(x + 14) (nghìn đồng).
0,25
Vì tổng số tiền bán rau thu hoạch từ thửa đất đó 950 (nghìn đồng) nên có
phương trình 10x(x + 14) = 950
x
2
+ 14x − 95 = 0 (1)
0,25
4
0
= 7
2
− 1(−95) = 144 > 0
0,25
Phương trình (1) có hai nghiệm phân biệt là
x
1
=
−7 +
√
144
1
= 5 (nhận), x
2
=
−7 −
√
144
1
= −19 (loại).
0,25
Thửa đất hình chữ nhật đã cho có chiều rộng 5 m, chiều dài 19 m.
0,25
3. 1,00
1)
Lập bảng tần số:
0,50
Trang 2
Đề thi học kì 2 Toán 9 Sở GD&ĐT Đồng Nai 2025
VnDoc xin giới thiệu Đề thi học kì 2 Toán 9 Sở GD&ĐT Đồng Nai 2025. Tài liệu gồm 5 câu hỏi tự luận giúp các bạn học sinh ôn tập, củng cố kiến thức chuẩn bị tốt cho kì thi đề thi Toán 9 học kì 2 sắp tới.
Để chuẩn bị cho kì thi học kì 2 lớp 9, mời các bạn vào chuyên mục Đề thi học kì 2 lớp 9 trên VnDoc. Chuyên mục tổng hợp đề thi của tất cả các môn, là tài liệu phong phú và hữu ích cho các em ôn tập và luyện đề. Đây cũng là tài liệu hay cho thầy cô tham khảo ra đề. Mời thầy cô và các em tham khảo.
