Giải Toán 9 trang 71 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 71 Tập 1 Chân trời
Giải Toán 9 trang 71 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 71.
Bài 1 Trang 71 Toán 9 tập 1 Chân trời
Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và 
\(\widehat {BAC} =68^{\circ}\) (Hình 10).
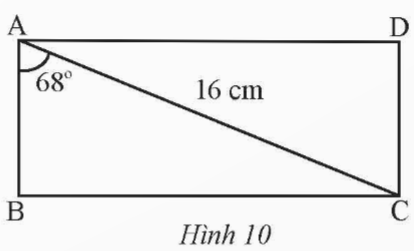
Hướng dẫn giải:
Xét tam giác ABC vuông tại B (do ABCD là hình chữ nhật), ta có:
AD = BC = AC . sin \(\widehat {BAC}\)
= 16 . sin 68o ≈ 14,8 cm
CD = AB = AC . cos \(\widehat {BAC}\)
= 16 . cos 68o ≈ 6,0 cm
Bài 2 Trang 71 Toán 9 tập 1 Chân trời
Cho tam giác ABC có BC = 20 cm, \(\widehat {ABC} =22^{\circ} ,\ \widehat {ACB}=30^{\circ}\)
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
b) Tính các cạnh và các góc còn lại của tam giác ABC.
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
Hướng dẫn giải:
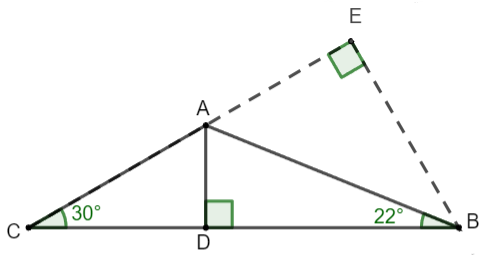
a) Xét tam giác BCE vuông tại E, ta có:
BE = BC . sin C = 20 . sin 30o = 10 cm
\(CE=\sqrt{BC^2-BE^2}=\sqrt{20^2-10^2}\approx17,3\) cm
Vậy khoảng cách từ điểm B đến đường thẳng AC là 10 cm.
b) Ta có: \(\widehat{EBC}=\widehat{CAD} = 60^{\circ}\)
Suy ra \(\widehat{EBA}=\widehat{EBC} - \widehat{ABC}= 60^{\circ}-22^{\circ} =38^{\circ}\)
Xét tam giác AEB vuông tại E, ta có:
- AE = EB . tan EBA ≈ 10 . tan 38o ≈ 7,8 cm
- EB = AB . cos EBA
\(\Rightarrow AB=\frac{EB}{\cos EBA}\approx\frac{10}{\sin38^{\circ} }\approx 12,7\) cm
- AC = EC - EA ≈ 17,3 - 7,8 ≈ 9,5 cm
Xét tam giác ABC ta có:
\(\widehat{BAC}=180^{\circ}- \widehat{ABC} - \widehat{ACB}\)
= 180o - 22o - 30o =128o
c) Xét tam giác ACD vuông tại D, ta có:
AD = AC . sin C = 9,5 . sin 30o = 4,8 cm
Bài 3 Trang 71 Toán 9 tập 1 Chân trời
Một người đẩy một vật lên hết một con dốc nghiêng một góc 35o (Hình 11). Tính độ cao của vật so với mặt đất biết độ dài con dốc là 4 m.
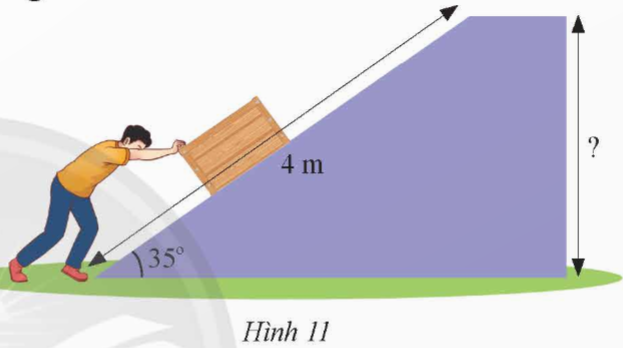
Hướng dẫn giải:
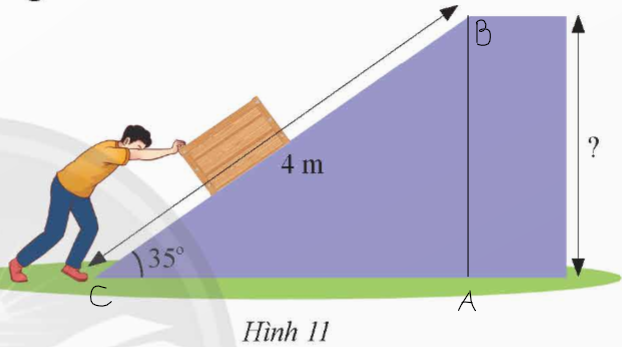
Xét tam giác ABC vuông tại A, ta có:
AB = BC . sin C = 4 . sin 35o ≈ 2,3 m
Vậy độ cao của vật so với mặt đất khoảng 2,3 m.
Bài 4 Trang 71 Toán 9 tập 1 Chân trời
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m, \(\widehat {A} =6^{\circ} ,\ \widehat {B} =4^{\circ}\).
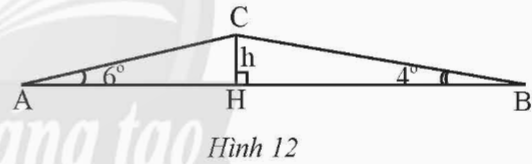
a) Tính chiều cao h của con dốc.
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.
Hướng dẫn giải:
a) Xét tam giác ACH vuông tại H, ta có:
AH = CH . cot A = h . cot 6o ≈ 9,5 . h
Xét tam giác BCH vuông tại H, ta có:
BH = CH . cot B = h . cot 4o ≈ 14,3 . h
Mặt khác: AH + HB = AB
⇒ 9,5h + 14,3h ≈ 762
⇒ 23,8h ≈ 762
⇒ h ≈ 32,0 m
b) Xét tam giác ACH vuông tại H, ta có:
CH = AC . sin A
\(\Rightarrow AC=\frac{CH}{\sin A}\approx\frac{32}{\sin6^{\circ} }\approx306,1\) m = 0,3061 km
Xét tam giác BCH vuông tại H, ta có:
BH = BC . sin B
\(\Rightarrow BC=\frac{CH}{\sin B}\approx\frac{32}{\sin4^{\circ} }\approx458,7\) m = 0,4587 km
Thời gian An đi từ nhà đến trường là:
\(\frac{306,1}{4}+\frac{458,7}{19}\approx0,1\) (giờ) = 6 phút
Vậy An đến trường lúc: 6 giờ + 6 phút = 6 giờ 6 phút
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 72 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 71 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông, được VnDoc biên soạn và đăng tải!
