Giải Toán 9 trang 60 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 60 Tập 1 Chân trời
Giải Toán 9 trang 60 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 60.
Hoạt động 1 Trang 60 Toán 9 tập 1 Chân trời
Cho góc nhọn 
\(\widehat{mOn} =\alpha\). Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với On và Om lần lượt tại B và B'.
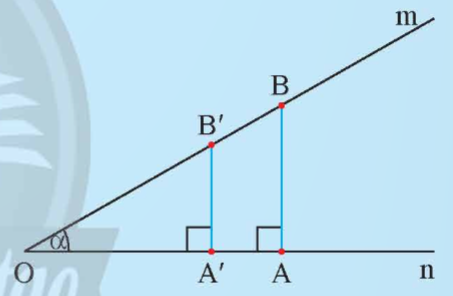
a) Có nhận xét gì về hai tam giác OAB và OA'B'?
b) So sánh các cặp tỉ số:
\(\frac{AB}{OA}\) và \(\frac{A'B'}{OA'}\); \(\frac{AB}{OA}\) và \(\frac{A'B'}{OB'}\); \(\frac{OA}{OB}\) và \(\frac{OA'}{OB'}\)
Hướng dẫn giải:
a) Ta có A'B' ⊥ On và AB ⊥ On nên A'B' // AB
Do đó tam giác OA'B' ∽ tam giác OAB
b) Ta có Δ OA'B' ∽ Δ OAB
\(\Rightarrow \frac{OA'}{OA}=\frac{A'B'}{AB}=\frac{OB'}{OB}\)
Do đó \(\frac{AB}{OA} =\frac{A'B'}{OA'}\); \(\frac{AB}{OA}=\frac{A'B'}{OB'}\); \(\frac{OA}{OB}=\frac{OA'}{OB'}\)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 61 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 60 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài tập cuối chương 3, được VnDoc biên soạn và đăng tải!
