Giải Toán 9 trang 93 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 93 Tập 1 Chân trời
Giải Toán 9 trang 93 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 93.
Thực hành 3 Trang 93 Toán 9 tập 1 Chân trời
Trên cung AB có số đo 90o của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15o. Tính số đo của cung MB.
Hướng dẫn giải:
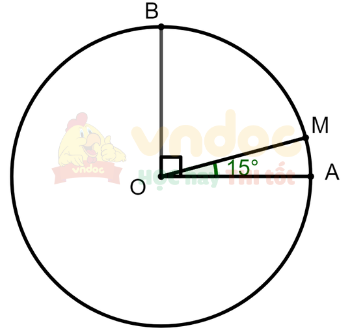
Ta có M thuộc cung AB nên tia OM nằm giữa hai tia OA và OB.
Do đó sđ 
\(\text{sđ}\overset{\frown}{{AB}} = \text{sđ}\overset{\frown}{{AM}}+\text{sđ}\overset{\frown}{{MB}}\)
Vậy \(\text{sđ}\overset{\frown}{{MB}} =\text{sđ}\overset{\frown}{{AB}} - \text{sđ}\overset{\frown}{{AM}}=90^{\circ} - 15^{\circ} = 75^{\circ}\)
Vận dụng 3 Trang 93 Toán 9 tập 1 Chân trời
Bạn Hùng làm một cái diều với thân diều là hình tứ giác SAOB sao cho OS là đường phân giác của \(\widehat{AOB}\) và \(\widehat{ASB}=106^{\circ}\). Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của \(\overset{\frown}{{AB}}\).
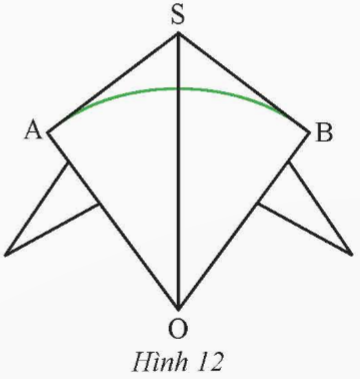
Hướng dẫn giải:
Do SA và SB là hai tiếp tuyến của (O) nên SA ⊥ OA và SB ⊥ OB
Suy ra \(\widehat{OAS}=\widehat{OBS}=90^{\circ}\)
Xét tứ giác SAOB ta có:
\(\widehat{OAS}+\widehat{ASB}+\widehat{OBS}+\widehat{AOB}=360^{\circ}\)
Suy ra \(\widehat{AOB}=360^{\circ}-90^{\circ}-106^{\circ}-90^{\circ}=74^{\circ}\)
Vậy \(\text{sđ} \overset{\frown}{AB} =\widehat{AOB}=74^{\circ}\)
Hoạt động 5 Trang 93 Toán 9 tập 1 Chân trời
Quan sát Hình 13. Hãy cho biết trong các góc \(\widehat{APB},\ \widehat{AOB},\ \widehat{AMB},\ \widehat{AQB}\), góc nào có đỉnh nằm trên đường tròn.
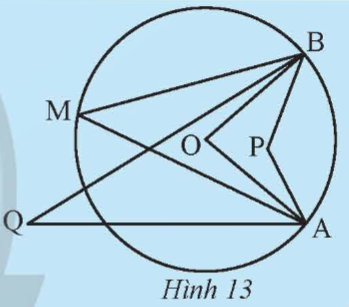
Hướng dẫn giải:
Góc có đỉnh bên trong đường tròn là: \(\widehat{AMB}\) vì M nằm trên đường tròn.
Thực hành 4 Trang 93 Toán 9 tập 1 Chân trời
Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.
Hướng dẫn giải:
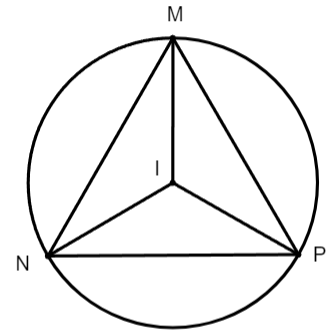
Các góc nội tiếp của đường tròn (I) là: \(\widehat{MNP},\ \widehat{NMP},\ \widehat{MPN}\)
Vì MNP là tam giác đều nên \(\widehat{MNP}= \widehat{NMP}= \widehat{MPN} =60^{\circ}\)
Vận dụng 4 Trang 93 Toán 9 tập 1 Chân trời
Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Hướng dẫn giải:
Lấy điểm A bất kì trên đường tròn (O)
Ta có \(\widehat{EAF}\) là góc nội tiếp chắn cung EF nên có vô số góc nội tiếp chắn cung EF.
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 94 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 93 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Góc ở tâm, góc nội tiếp, được VnDoc biên soạn và đăng tải!
