VnDoc.com

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Giải bài tập SGK Toán lớp 9 trang 48, 49 SGK

Bài trước

Bài sau

Giải bài tập Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn là tài liệu tham khảo hữu ích dành cho thầy cô trong quá trình giảng dạy, ôn luyện kiến thức đã học cho các bạn đồng thời cũng giúp học sinh học tốt môn Toán lớp 9. Mời các bạn tham khảo

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 48: Từ bảng kết luận của bài trước hãy dùng các đẳng thức $b=2b’,Δ=4Δ’$ để suy ra những kết luận sau:

Lời giải

Với $b=2b’,Δ=4Δ’$ ta có:

a) Nếu Δ' > 0 thì Δ > 0 phương trình có hai nghiệm

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

b) Nếu Δ' = 0 thì Δ = 0 phương trình có nghiệm kép

$x=\frac{-b}{2a}=\frac{-2b$ $x=\frac{-b}{2a}=\frac{-2b'}{2a}=\frac{-b'}{a}$

c) Nếu Δ' < 0 thì Δ < 0 do đó phương trình vô nghiệm.

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 48: Giải phương trình $5x^2+4x-1=0$ bằng cách điền vào những chỗ trống:

$a=\dots;b’=\dots;c=\dots;$ $a=\dots;b’=\dots;c=\dots;$

$Δ’=\dots;\sqrt{Δ$ $Δ’=\dots;\sqrt{Δ'}=\dots.$

Nghiệm của phương trình:

$x_1=\dots;x_2=\dots.$ $x_1=\dots;x_2=\dots.$

Lời giải

$a=5;b’=2;c=-1;$

$Δ’=9;\sqrt{Δ$ $Δ’=9;\sqrt{Δ'}=3$

Nghiệm của phương trình:

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 49: Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình:

a) $3x^2+8x+4=0$;

b) $7x^2-6\sqrt{2}x+2=0$ $7x^2-6\sqrt{2}x+2=0$.

Lời giải

a) $3x^2+8x+4=0$;

$a=3;b'=4;c=4$

$Δ'=b'^2-ac=4^2-3.4=4⇒\sqrt{Δ'}=2$

Phương trình có 2 nghiệm:

$x_1=\frac{-4+2}{3}=\frac{-2}{3};x_2=\frac{-4-2}{3}=-2$ $x_1=\frac{-4+2}{3}=\frac{-2}{3};x_2=\frac{-4-2}{3}=-2$

b) $7x_2-6\sqrt{2x}+2=0$ $7x_2-6\sqrt{2x}+2=0$

$a=7;b'=-3\sqrt{2};c=2$

$Δ'=b'^2-ac=\left(-3\sqrt{2}\right)^2-7.2=4⇒\sqrt{Δ'}=2$

Phương trình có 2 nghiệm:

$x_1=\frac{3\sqrt{2}+2}{7};x_2=\frac{3\sqrt{2}-2}{7}$ $x_1=\frac{3\sqrt{2}+2}{7};x_2=\frac{3\sqrt{2}-2}{7}$

Trả lời câu hỏi Toán 9 Tập 2 Bài 5 trang 49: Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình:

a) $3x^2+8x+4=0;$

b) $7x^2-6\sqrt{2x}+2=0.$ $7x^2-6\sqrt{2x}+2=0.$

Lời giải

a) $3x^2+8x+4=0$;

$a=3;b'=4;c=4$

$Δ'=b'^2-ac=4^2-3.4=4⇒\sqrt{Δ'}=2$

Phương trình có 2 nghiệm:

$x_1=\frac{-4+2}{3}=\frac{-2}{3};x_2=\frac{-4-2}{3}=-2$ $x_1=\frac{-4+2}{3}=\frac{-2}{3};x_2=\frac{-4-2}{3}=-2$

b) $7x^2-6\sqrt{2x}+2=0$ $7x^2-6\sqrt{2x}+2=0$

$a=7;b'=-3\sqrt{2};c=2$

$Δ'=b'^2-ac=\left(-3\sqrt{2})^2-7.2=4⇒\sqrt{Δ'}=2\right)$

Phương trình có 2 nghiệm:

$x_1=\frac{3\sqrt{2}+2}{7};x_2=\frac{3\sqrt{2}-2}{7}$ $x_1=\frac{3\sqrt{2}+2}{7};x_2=\frac{3\sqrt{2}-2}{7}$

Giải bài 17 trang 49 SGK Toán 9 tập 2. Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:

Đề bài

Xác định $a, b', c$ rồi dùng công thức nghiệm thu gọn giải các phương trình:

a) $4{x^2} + 4x + 1 = 0$ $4{x^2} + 4x + 1 = 0$;

b) $13852{x^2} - 14x + 1 = 0$ $13852{x^2} - 14x + 1 = 0$;

c) $5{x^2} - 6x + 1 = 0$ $5{x^2} - 6x + 1 = 0$;

d) $- 3{x^2} + 4\sqrt 6 x + 4 = 0$ $- 3{x^2} + 4\sqrt 6 x + 4 = 0$.

Lời giải chi tiết

a) $4{x^2} + 4x + 1 = 0$ $4{x^2} + 4x + 1 = 0$

Ta có: $a = 4,\ b$ $a = 4,\ b' = 2,\ c = 1$

Suy ra $\Delta$ $\Delta' = {2^2} - 4.1 = 0$

Do đó phương trình có nghiệm kép:

${x_1} = {x_2} = \dfrac{ - 2}{4} = - \dfrac{1 }{ 2}$ ${x_1} = {x_2} = \dfrac{ - 2}{4} = - \dfrac{1 }{ 2}$.

b) $13852{x^2} - 14x + 1 = 0$ $13852{x^2} - 14x + 1 = 0$

Ta có: $a = 13852,\ b$ $a = 13852,\ b' = - 7,\ c = 1$

Suy ra $\Delta$ $\Delta' = {( - 7)^2} - 13852.1 = - 13803 < 0$

Do đó phương trình vô nghiệm.

c) $5{x^2} - 6x + 1 = 0$ $5{x^2} - 6x + 1 = 0$

Ta có: $a = 5,\ b$ $a = 5,\ b' = - 3,\ c = 1$

Suy ra $\Delta$ $\Delta ' = {( - 3)^2} - 5.1 = 4 > 0$.

Do đó phương trình có hai nghiệm phân biệt:

${x_1} = \dfrac{3 + \sqrt 4}{5}=\dfrac{5}{5} = 1$ ${x_1} = \dfrac{3 + \sqrt 4}{5}=\dfrac{5}{5} = 1$

${x_2} = \dfrac{3 - \sqrt 4}{5}=\dfrac{1}{5}.$ ${x_2} = \dfrac{3 - \sqrt 4}{5}=\dfrac{1}{5}.$

d) $- 3{x^2} + 4\sqrt 6 x + 4 = 0$ $- 3{x^2} + 4\sqrt 6 x + 4 = 0$

Ta có: $a = - 3,\ b$ $a = - 3,\ b' = 2\sqrt 6 ,\ c = 4$

Suy ra $\Delta$ $\Delta ' = {(2\sqrt 6 )^2} - ( - 3).4 = 36 > 0$

Do đó phương trình có hai nghiệm phân biệt:

${x_1} = \dfrac{ - 2\sqrt 6 + 6}{ - 3} = \dfrac{2\sqrt 6 - 6}{3}$ ${x_1} = \dfrac{ - 2\sqrt 6 + 6}{ - 3} = \dfrac{2\sqrt 6 - 6}{3}$

${x_2} = \dfrac{ - 2\sqrt 6 - 6}{ - 3} = \dfrac{2\sqrt {6 }+6 }{3}$ ${x_2} = \dfrac{ - 2\sqrt 6 - 6}{ - 3} = \dfrac{2\sqrt {6 }+6 }{3}$

Giải bài 18 trang 49 SGK Toán 9 tập 2. Đưa các phương trình sau về dạng

Đề bài

Đưa các phương trình sau về dạng $ax^2 + 2b’x + c = 0$ và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):

a) $3{x^2} - 2x = {x^2} + 3$ $3{x^2} - 2x = {x^2} + 3$;

b) ${(2x - \sqrt 2 )^2} - 1 = (x + 1)(x - 1)$ ${(2x - \sqrt 2 )^2} - 1 = (x + 1)(x - 1)$;

c) $3{x^2} + 3 = 2(x + 1)$ $3{x^2} + 3 = 2(x + 1)$;

d) $0,5x(x + 1) = {(x - 1)^2}$ $0,5x(x + 1) = {(x - 1)^2}$.

1) Triển khai đưa hết các số hạng sang vế trái và thu gọn, vế phải bằng $0$.

2) Xét phương trình: $ax^2+bx+c=0 (a \ne 0)$ $ax^2+bx+c=0 (a \ne 0)$ với $b=2b'$ và biệt thức: $\Delta$ $\Delta' =b'^2-ac$

+) Nếu $\Delta$ $\Delta' > 0$ thì phương trình có hai nghiệm phân biệt:

$x_1=\dfrac{-b$ $x_1=\dfrac{-b'+\sqrt{\Delta'}}{a};\ x_2=\dfrac{-b'-\sqrt{\Delta'}}{a}$

+) Nếu $\Delta$ $\Delta' < 0$ thì phương trình vô nghiệm.

+) Nếu $\Delta$ $\Delta' =0$ thì phương trình có nghiệm kép: $x_1=x_2=\dfrac{-b$ $x_1=x_2=\dfrac{-b'}{a}$.

Lời giải chi tiết

a) $3{x^2} - 2x = {x^2} + 3$ $3{x^2} - 2x = {x^2} + 3$

$\Leftrightarrow 3{x^2} - 2x - {x^2} - 3=0$ $\Leftrightarrow 3{x^2} - 2x - {x^2} - 3=0$

$\Leftrightarrow 2{x^2} - 2x - 3 = 0$ $\Leftrightarrow 2{x^2} - 2x - 3 = 0$

Suy ra $a=2, b'=-1,c=-3$

$\Rightarrow \Delta$ $\Rightarrow \Delta ' = {( - 1)^2} - 2.( - 3) = 7 > 0.$

Do đó phương trình có hai nghiệm phân biệt:

${x_1} = \dfrac{1 + \sqrt 7 }{2} \approx 1,82$ ${x_1} = \dfrac{1 + \sqrt 7 }{2} \approx 1,82$

${x_2} = \dfrac{1 - \sqrt 7 }{2} \approx - 0,82$ ${x_2} = \dfrac{1 - \sqrt 7 }{2} \approx - 0,82$

b) ${(2x - \sqrt 2 )^2} - 1 = (x + 1)(x - 1)$ ${(2x - \sqrt 2 )^2} - 1 = (x + 1)(x - 1)$

$\Leftrightarrow 4x^2-4\sqrt 2 x + 2- 1 = x^2 -1$ $\Leftrightarrow 4x^2-4\sqrt 2 x + 2- 1 = x^2 -1$

$\Leftrightarrow 4x^2-4\sqrt 2 x + 2 - 1 - x^2 +1=0$ $\Leftrightarrow 4x^2-4\sqrt 2 x + 2 - 1 - x^2 +1=0$

$\Leftrightarrow 3{x^2} - 4\sqrt 2 x + 2 = 0$ $\Leftrightarrow 3{x^2} - 4\sqrt 2 x + 2 = 0$

$a=3,b'=-2\sqrt{2},c=2$

$\Rightarrow \Delta$ $\Rightarrow \Delta ' = {( - 2\sqrt 2 )^2} - 3.2 = 2 > 0$

Do đó phương trình có hai nghiệm phân biệt:

$x_1=\frac{2\sqrt{2}+\sqrt{2}}{3}=\sqrt{2}\approx 1,41$ $x_1=\frac{2\sqrt{2}+\sqrt{2}}{3}=\sqrt{2}\approx 1,41$

$x_1=\frac{2\sqrt{2}+\sqrt{2}}{3}=\sqrt{2}\approx 1,41$ $x_1=\frac{2\sqrt{2}+\sqrt{2}}{3}=\sqrt{2}\approx 1,41$ $x_2=\frac{2\sqrt{2}-\sqrt{2}}{3}=\frac{\sqrt{2}}{3}\approx0,47$ $x_2=\frac{2\sqrt{2}-\sqrt{2}}{3}=\frac{\sqrt{2}}{3}\approx0,47$

c) $3{x^2} + 3 = 2(x + 1)$ $3{x^2} + 3 = 2(x + 1)$

$\Leftrightarrow 3{x^2} +3- 2x -2 = 0$ $\Leftrightarrow 3{x^2} +3- 2x -2 = 0$

$\Leftrightarrow 3{x^2} - 2x +1 = 0$ $\Leftrightarrow 3{x^2} - 2x +1 = 0$

Suy ra $a=3,b'=-1,c=1$

$\Rightarrow\triangle$ $\Rightarrow\triangle'\left(-1\right)^2-3.1=-2<0$

Do đó phương trình vô nghiệm.

d) $0,5x(x + 1) = {(x - 1)^2}$ $0,5x(x + 1) = {(x - 1)^2}$

$\Leftrightarrow 0,5x^2 + 0,5x = x^2-2x+1$ $\Leftrightarrow 0,5x^2 + 0,5x = x^2-2x+1$

$\Leftrightarrow0,5x^2+0,5x-x^2+2x-1=0$ $\Leftrightarrow0,5x^2+0,5x-x^2+2x-1=0$

$\Leftrightarrow -0,5 x^2 +2,5 x -1 = 0$ $\Leftrightarrow -0,5 x^2 +2,5 x -1 = 0$

$\Leftrightarrow x^2-5x+2=0$ $\Leftrightarrow x^2-5x+2=0$

Suy ra $a=1;\ b$ $a=1;\ b'=-2,5;\ c=2$

$\Rightarrow \Delta$ $\Rightarrow \Delta ' = {( - 2,5)^2} - 1.2 = 4,25 > 0$

Do đó phương trình có hai nghiệm phân biệt:

$x_1=2,5+\sqrt{4,25}\approx4,56$ $x_1=2,5+\sqrt{4,25}\approx4,56$

$x_2=2,5-\sqrt{4,25}\approx0,44$ $x_2=2,5-\sqrt{4,25}\approx0,44$

(Rõ ràng trong trường hợp này dùng công thức nghiệm thu gọn cũng không đơn giản hơn)

Bài 19 (trang 49 SGK Toán 9 tập 2): Đố. Đố em biết vì sao khi a > 0 và phương trình $ax^2+bx+c=0$ vô nghiệm thì $ax^2+bx+c>0$ với mọi giá trị của x?

Lời giải

Ta có: a > 0 (gt), Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn với mọi x, a, b ⇒

Phương trình $ax^2+bx+c$ vô nghiệm nên Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Vậy $ax^2+bx+c$ = Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn với mọi x.

Luyện tập (trang 49-50)

Bài 20 (trang 49 SGK Toán 9 tập 2): Giải các phương trình:

a) $25x^2-16=0$;

b) $2x^2+3=0$;

c) $4,2x^2+5,46x=0$;

d) $4x2-2\sqrt{3}.x=1-\sqrt{3}$ $4x2-2\sqrt{3}.x=1-\sqrt{3}$.

Lời giải

Phương trình vô nghiệm vì x² ≥ 0 với mọi x.

c) $4,2x^2+5,46x=0$

$⇔x.(4,2x+5,46)=0$

⇔ x = 0 hoặc $4,2x+5,46=0$

$+4,2x+5,46=0⇔$

Vậy phương trình có hai nghiệm x₁ = 0 và

d) $4x^2-2\sqrt{3}x=1-\sqrt{3}$ $4x^2-2\sqrt{3}x=1-\sqrt{3}$.

$⇔4x^2-2\sqrt{3}x-1+\sqrt{3}=0$ $⇔4x^2-2\sqrt{3}x-1+\sqrt{3}=0$

Có $a=4;b’=-\sqrt{3};c=-1+\sqrt{3}$ $a=4;b’=-\sqrt{3};c=-1+\sqrt{3}$;

$Δ’=b'^2-ac=(-\sqrt{3})^2-4(-1+\sqrt{3})=7-4\sqrt{3}=4-2.2.\sqrt{3}+(\sqrt{3})^2=(2-\sqrt{3})^2$

Phương trình có hai nghiệm phân biệt:

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Bài 21 (trang 49 SGK Toán 9 tập 2): Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26):

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Lời giải

a) $x^2=12x+288$

$⇔x^2-12x-288=0$

Có $a=1;b’=-6;c=-288;Δ’=b’^2-ac=(-6)^2-1.(-288)=324>0$

Phương trình có hai nghiệm:

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Vậy phương trình có hai nghiệm x₁ = 24 và x₂ = -12.

b)

$⇔x^2+7x=228$

$⇔x^2+7x-228=0$

Có $a=1;b=7;c=-228;Δ=b^2-4ac=7^2-4.1.(-228)=961>0$

Phương trình có hai nghiệm:

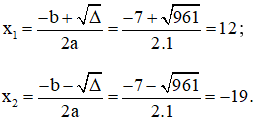
Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Vậy phương trình có hai nghiệm x₁ = 12 và x₂ = -19.

Bài 22 (trang 49 SGK Toán 9 tập 2): Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?

Lời giải

a) Phương trình $15x^2+4x-2005=0cóa=15;c=-2005$ trái dấu

⇒ Phương trình có hai nghiệm phân biệt.

b) Phương trình có ; c = 1890 trái dấu

⇒ Phương trình có hai nghiệm phân biệt.

Bài 23 (trang 50 SGK Toán 9 tập 2): Rada của một máy bay trực thăng the dõi chuyển động của ôtô trong 10 phút, phát hiện rằng vận tốc v của ôtô they đổi phụ thuộc vào thời gian bởi công thức:

$v=3t^2-30t+135$

(t tính bằng phút, v tính bằng km/h)

a) Tính vận tốc của ôtô khi t = 5 phút.

b) Tính giá trị của t khi vận tốc ôtô bằng 120km/h (làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải

a) Tại t = 5, ta có: $v=3.5^2-30.5+135=60(km/h)$

b) Khi v = 120 km/h

$⇔3t^2-30t+135=120$

$⇔3t^2-30t+15=0$

Có $a=3;b’=-15;c=15;Δ’=b’^2-ac=(-15)^2-3.15=180$

Phương trình có hai nghiệm phân biệt

Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn

Vì rada quan sát chuyển động của ô tô trong 10 phút nên t₁ và t₂ đều thỏa mãn.

Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

Bài 24 (trang 50 SGK Toán 9 tập 2): Cho phương trình (ẩn x) $x^2-2(m-1)x+m^2=0$

a) Tính Δ'.

b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.

Lời giải

a) Phương trình $x^2-2(m-1)x+m^2=0(1)$

Có $a=1;b’=-(m-1);c=m^2$

$⇒Δ’=b'^2-ac=(1-m)^2-1.m^2=1-2m+m^2-m^2=1-2m.$

b) Phương trình (1):

+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > $\frac{1}{2}$ $\frac{1}{2}$

+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = $\frac{1}{2}$ $\frac{1}{2}$

+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < $\frac{1}{2}$ $\frac{1}{2}$

Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < $\frac{1}{2}$ $\frac{1}{2}$; có nghiệm kép khi m = $\frac{1}{2}$ $\frac{1}{2}$ và vô nghiệm khi m > $\frac{1}{2}$ $\frac{1}{2}$

....................................

Ngoài Giải bài tập SGK Toán lớp 9 bài 5: Công thức nghiệm thu gọn. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt