Giải Toán 9 trang 87 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 87 Tập 1 Chân trời
Giải Toán 9 trang 87 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 87.
Hoạt động 3 Trang 87 Toán 9 tập 1 Chân trời
Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).
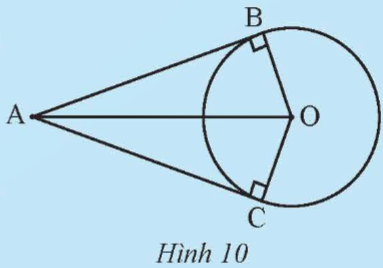
a) Chứng minh hai tam giác ABO và ACO bằng nhau.
b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.
Hướng dẫn giải:
a) Ta có AB và AC là các tiếp tuyến của đường tròn (O)
Suy ra AB ⊥ OB và AC ⊥ OC
Xét tam giác vuông ABO và tam giác vuông ACO có:
OB = OC = R
OA cạnh chung
Do đó, Δ ABO = Δ ACO (ch - cgv)
b) Ta có Δ ABO = Δ ACO (câu a)
Suy ra AB = AC (hai cạnh tương ứng)
và 
\(\widehat{OAB}=\widehat{OAC}; \ \widehat{AOB}=\widehat{AOC}\) (các góc tương ứng)
Thực hành 3 Trang 87 Toán 9 tập 1 Chân trời
Cho điểm M nằm ngooài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết \(\widehat{EMF}=60^{\circ}\).
a) Tính số đo \(\widehat{EMI}\) và \(\widehat{EIF}\).
b) Tính độ dài MI
Hướng dẫn giải:
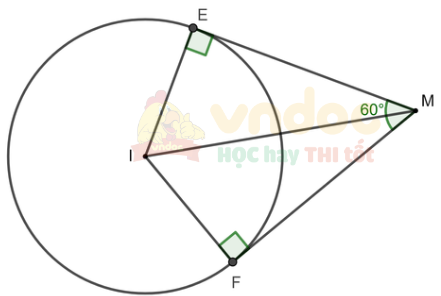
a) Hai tiếp tuyến tại E và F của đường tròn (O) cắt nhau tại M, suy ra MI là phân giác của \(\widehat{EMF}\)
Do đó: \(\widehat{EMI}=\frac{\widehat{EMF}}{ 2} =\frac{60^{\circ} }{2} =30^{\circ}\)
\(\widehat{EIF}=360^{\circ}-\widehat{IEM}-\widehat{IFM} -\widehat{EMF}\)
= 360o − 90o − 90o − 60o = 120o
b) Xét tam giác IEM vuông tại E, ta có:
IE = IM . sin \(\widehat{EMI}\)
Suy ra \(IM=\frac{IE}{\sin \widehat{IME}}=\frac{6}{\sin30}=12\) cm.
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 88 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 87 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Tiếp tuyến của đường tròn, được VnDoc biên soạn và đăng tải!
