Giải Toán 9 trang 102 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 102 Tập 1 Chân trời
Giải Toán 9 trang 102 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 102.
Bài 1 Trang 102 Toán 9 tập 1 Chân trời
Tính độ dài các cung 30o; 90o; 120o của đường tròn (O; 6 cm)
Hướng dẫn giải:
Cung 30o, bán kính R = 6 cm có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.30}}{{180}} = \pi \approx 3,14\) cm
Cung 900, bán kính R = 6 cm có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.90}}{{180}} = 3\pi\approx9,42\) cm
Cung 120o, bán kính R = 6 cm có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.120}}{{180}} = 4\pi \approx12,57\) cm
Bài 2 Trang 102 Toán 9 tập 1 Chân trời
Tính diện tích hình quạt tròn ứng với cung số đo lần lượt là 30o; 90o; 120o của hình tròn (O; 12 cm).
Hướng dẫn giải:
Diện tích của hình quạt tròn bán kính R = 12 cm, ứng với cung 30o là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.12}^2}.30}}{{360}} =12\pi \approx 37,70\) (cm2)
Diện tích của hình quạt tròn bán kính R = 12 cm, ứng với cung 90o là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.12}^2}.90}}{{360}} =36\pi \approx 113,1\) (cm2)
Diện tích của hình quạt tròn bán kính R = 12 cm, ứng với cung 120o là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.12}^2}.120}}{{360}} =48\pi\approx 150,8\) (cm2)
Bài 3 Trang 102 Toán 9 tập 1 Chân trời
Tính diện tích hình quạt tròn ứng với cung có độ dài lần lượt là 8 cm, 15 cm của hình tròn (O; 5 cm).
Hướng dẫn giải:
Ta có: \(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{R.\pi Rn}}{{2.180}} =\frac{{Rl}}{{2}}\)
Diện tích của hình quạt tròn bán kính R = 5 cm, ứng với cung có độ dài 8 cm có diện tích là:
\(S = \frac{{R.l}}{2} = \frac{{5.8}}{2} = 20\) (cm2)
Diện tích của hình quạt tròn bán kính R = 5 cm, ứng với cung có độ dài 15 cm có diện tích là:
\(S = \frac{{R.l}}{2} = \frac{{5.15}}{2} = 37,5\) (cm2)
Bài 4 Trang 102 Toán 9 tập 1 Chân trời
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 9 cm) và (O; 12 cm).
Hướng dẫn giải:
Hình vành khuyên giới hạn bởi (O; 9 cm) và (O; 12 cm) có diện tích là:
S = π(R2 – r2) = π.(122 – 92) = 63π ≈ 197,92 (cm2)
Bài 5 Trang 102 Toán 9 tập 1 Chân trời
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo là 95° (Hình 12).
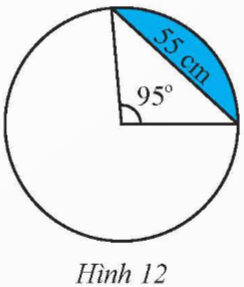
Hướng dẫn giải:
Bài 6 Trang 102 Toán 9 tập 1 Chân trời
Một máy kéo nông nghiệp có đường kính bánh xe sau là 124 cm và đường kính bánh xe trước là 80 cm. Hỏi khi bánh xe sau lăn được 20 vòng thì bánh xe trước lăn được bao nhiêu vòng?
Hướng dẫn giải:
Chu vi của bánh xe sau là:
π . d = 124π (cm)
Chu vi của bánh xe trước là:
π . d' = 80π (cm)
Sau khi lăn được 20 vòng thì bánh xe sau đi được quãng đường là:
124π . 20 = 2 480π (cm)
Khi đó, bánh xe trước lăn được số vòng là:
2 480π : 80π = 31 (vòng)
Bài 7 Trang 102 Toán 9 tập 1 Chân trời
Thành phố Đà Lạt nằm vào khoảng 11o 58' vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km. Hãy tính độ dài cung kinh tuyến từ Đà Lạt đến xích đạo.
(Nguồn: https://vi.wikipedia.org/wiki/Đà-Lạt.)
Hướng dẫn giải:
Ta có mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km, nghĩa là chu vi một vòng kinh tuyến khoảng 40 000 km.
Do đó bán kính của Trái Đất là:
\(R=\frac{C}{2\pi}\approx\frac{20\ 000}{\pi}\) (km)
Đổi \(11^{\circ} 58'=\left(11+\frac{58}{60}\right)^{\circ} =\left(\frac{359}{30}\right) ^{\circ}\)
Độ dài cung kinh tuyến từ Đà Lạt đến xích đạo là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{ \pi.\frac{20\ 000}{\pi} .\left (\frac{359}{30} \right ) }}{{180}} \approx 1329,63\) (km)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 103 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 102 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 4: Hình quạt tròn và hình vành khuyên, được VnDoc biên soạn và đăng tải!
