Toán 9 Chân trời sáng tạo Bài 1: Căn bậc hai
Giải Toán 9 Chân trời sáng tạo Bài 1: Căn bậc hai hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 37, 38, 39, 40, 41, giúp các em nắm vững kiến thức được học, luyện tập giải môn Toán lớp 9.
Giải Toán 9 CTST bài 1: Căn bậc hai
- Giải Toán 9 trang 37
- Giải Toán 9 trang 38
- Giải Toán 9 trang 39
- Giải Toán 9 trang 40
- Giải Toán 9 trang 41
- Bài 1 trang 41 Toán 9 Chân trời sáng tạo
- Bài 2 trang 41 Toán 9 Chân trời sáng tạo
- Bài 3 trang 41 Toán 9 Chân trời sáng tạo
- Bài 4 trang 41 Toán 9 Chân trời sáng tạo
- Bài 5 Trang 41 Toán 9 tập 1 Chân trời
- Bài 6 Trang 41 Toán 9 tập 1 Chân trời
- Bài 7 Trang 41 Toán 9 tập 1 Chân trời
- Bài 9 Trang 41 Toán 9 tập 1 Chân trời
Giải Toán 9 trang 37
Hoạt động 1 trang 37 SGK Toán 9 Chân trời sáng tạo
Cho trục số được vẽ trên lưới ô vuông đơn vị như Hình 1.
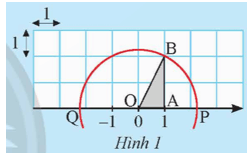
a) Tính độ dài cạnh huyền OB của tam giác vuông OAB.
b) Vẽ đường tròn tâm O bán kính OB, đường tròn này cắt trục số tại hai điểm P và Q.
Gọi x là số thực được biểu diễn bởi điểm P, y là số thực được biểu diễn bởi điểm Q.
Thay mỗi ? bằng số thích hợp để có các đẳng thức:
x2 = ?, y2 = ?.
Hướng dẫn giải
a) Áp dụng định lí Pythagore vào tam giác vuông OAB ta có:
![]() \(OB = \sqrt {1 + {2^2}} = \sqrt 5\)
\(OB = \sqrt {1 + {2^2}} = \sqrt 5\)
b) Vì P, Q là hai điểm thuộc đường tròn tâm O bán kính OB nên OP = OQ = OB = ![]() \(\sqrt 5\)
\(\sqrt 5\)
Vì x là số thực được biểu diễn bởi điểm P nên x = ![]() \(\sqrt 5\),
\(\sqrt 5\),
y là số thực được biểu diễn bởi điểm Q nên y = - ![]() \(\sqrt 5\).
\(\sqrt 5\).
Khi đó ta có các đẳng thức:
![]() \({x^2} = {\left( {\sqrt 5 } \right)^2} = 5\)
\({x^2} = {\left( {\sqrt 5 } \right)^2} = 5\)
![]() \({y^2} = {\left( {-\sqrt 5 } \right)^2} = 5\)
\({y^2} = {\left( {-\sqrt 5 } \right)^2} = 5\)
Giải Toán 9 trang 38
Thực hành 1 trang 38 SGK Toán 9 Chân trời sáng tạo
Tính các căn bậc hai của mỗi số sau:
a) 36
b) ![]() \(\frac{4}{{49}}\)
\(\frac{4}{{49}}\)
c) 1,44
d) 0
Hướng dẫn giải
a) Ta có 62 = 36, nên 36 có hai căn bậc hai là 6 và – 6
b) Ta có ![]() \({\left( {\frac{2}{7}} \right)^2}= \frac{4}{{49}},\) nên
\({\left( {\frac{2}{7}} \right)^2}= \frac{4}{{49}},\) nên ![]() \(\frac{4}{{49}}\) có hai căn bậc hai là
\(\frac{4}{{49}}\) có hai căn bậc hai là ![]() \(\frac{2}{7} và - \frac{2}{7}\)
\(\frac{2}{7} và - \frac{2}{7}\)
c) Ta có (1,2)2 = 1,44 nên 1,44 có hai căn bậc hai là 1,2 và – 1,2
d) Số 0 chỉ có một căn bậc hai là chính nó \sqrt 0 = 0
Thực hành 2 trang 38 SGK Toán 9 Chân trời sáng tạo
Sử dụng dấu căn bậc hai để viết các căn bậc hai của mỗi số:
a) 11
b) 2,5
c) – 0,09
Hướng dẫn giải
a) Các căn bậc hai của 11 là ![]() \(\sqrt {11}\) và -
\(\sqrt {11}\) và - ![]() \(\sqrt {11}\)
\(\sqrt {11}\)
b) Các căn bậc hai của 2,5 là ![]() \(\sqrt {2,5}\) và -
\(\sqrt {2,5}\) và -![]() \(\sqrt {2,5}\)
\(\sqrt {2,5}\)
c) Do – 0,09 là số âm nên nó không có căn bậc hai.
Thực hành 3 Trang 38 Toán 9 tập 1 Chân trời
Tính:
a) ![]() \(\sqrt{1600}\)
\(\sqrt{1600}\)
b) ![]() \(\sqrt{0,81}\)
\(\sqrt{0,81}\)
c) ![]() \(\sqrt{\frac{9}{25}}\)
\(\sqrt{\frac{9}{25}}\)
Hướng dẫn giải:
a) ![]() \(\sqrt{1600} = \sqrt{40^2}=40\)
\(\sqrt{1600} = \sqrt{40^2}=40\)
b) ![]() \(\sqrt{0,81} =\sqrt{0,9^2}=0,9\)
\(\sqrt{0,81} =\sqrt{0,9^2}=0,9\)
c)  \(\sqrt{\frac{9}{25}} =\sqrt{\left ( \frac{3}{5} \right )^2} = \frac{3}{5}\)
\(\sqrt{\frac{9}{25}} =\sqrt{\left ( \frac{3}{5} \right )^2} = \frac{3}{5}\)
Giải Toán 9 trang 39
Thực hành 4 Trang 39 Toán 9 tập 1 Chân trời
Tính giá trị của các biểu thức:
a) ![]() \(\left(\sqrt{12}\right)^2\)
\(\left(\sqrt{12}\right)^2\)
b) ![]() \(\left(-\sqrt{0,36}\right)^2\)
\(\left(-\sqrt{0,36}\right)^2\)
c) ![]() \(\left(\sqrt{5}\right)^2+\left(-\sqrt{1,21}\right)^2\)
\(\left(\sqrt{5}\right)^2+\left(-\sqrt{1,21}\right)^2\)
Hướng dẫn giải:
a) ![]() \(\left(\sqrt{12}\right)^2=12\)
\(\left(\sqrt{12}\right)^2=12\)
b) ![]() \(\left(-\sqrt{0,36}\right)^2=0,36\)
\(\left(-\sqrt{0,36}\right)^2=0,36\)
c) ![]() \(\left(\sqrt{5}\right)^2+\left(-\sqrt{1,21}\right)^2=5+1,21=6,21\)
\(\left(\sqrt{5}\right)^2+\left(-\sqrt{1,21}\right)^2=5+1,21=6,21\)
Vận dụng 1 trang 39 SGK Toán 9 Chân trời sáng tạo
Biết rằng hình A và hình vuông B trong Hình 2 có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.
Hướng dẫn giải
Xét hình A:
Ta có diện tích cả hình vuông cạnh 3cm là : 3.3 = 9 cm2
Ta có diện tích cả hình vuông cạnh ![]() \(\sqrt 2\)cm là :
\(\sqrt 2\)cm là : ![]() \(\sqrt 2 . \sqrt 2 = 2\) cm2
\(\sqrt 2 . \sqrt 2 = 2\) cm2
Suy ra diện tích hình A là: 9 – 2 = 7 cm2
Mà hình vuông B bằng diện tích hình A là 7 cm2
Nên x.x = x2 = 7 suy ra x = ![]() \(\sqrt 7\)cm.
\(\sqrt 7\)cm.
Thực hành 5 Trang 39 Toán 9 tập 1 Chân trời
Sử dụng máy tính cầm tay, tính gần đúng các số sau (kết quả làm tròn đến chữ số thập phân thứ ba):
a) ![]() \(\sqrt{11}\)
\(\sqrt{11}\)
b) ![]() \(\sqrt{7,64}\)
\(\sqrt{7,64}\)
c) ![]() \(\sqrt{\frac{2}{3}}\)
\(\sqrt{\frac{2}{3}}\)
Hướng dẫn giải:
a) ![]() \(\sqrt{11} \approx 3,317\)
\(\sqrt{11} \approx 3,317\)
b) ![]() \(\sqrt{7,64} \approx 2,764\)
\(\sqrt{7,64} \approx 2,764\)
c) ![]() \(\sqrt{\frac{2}{3}} \approx0,816\)
\(\sqrt{\frac{2}{3}} \approx0,816\)
Thực hành 6 Trang 39 Toán 9 tập 1 Chân trời
Sử dụng máy tính cầm tay để:
a) Tìm các căn bậc hai của 10,08 (kết quả làm tròn đến chữ số thập phân thứ tư)
b) Tính giá trị của biểu thức ![]() \(\frac{\sqrt{5}-1}{2}\) (kết quả làm tròn đến chữ số thập phân thứ năm)
\(\frac{\sqrt{5}-1}{2}\) (kết quả làm tròn đến chữ số thập phân thứ năm)
Hướng dẫn giải:
a) Các căn bậc hai của 10,08 là 3,1749 và − 3,1749
b) Giá trị của biểu thức ![]() \(\frac{\sqrt{5}-1}{2} \approx 0,61803\)
\(\frac{\sqrt{5}-1}{2} \approx 0,61803\)
Giải Toán 9 trang 40
Hoạt động 2 Trang 40 Toán 9 tập 1 Chân trời
Một chiếc thang dài 5 m tựa vào bức tường như Hình 3.

a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1; 2; 3; 4.
Hướng dẫn giải:
a) Áp dụng định lí Pythagore trong tam giác vuông, ta có chiều cao từ đỉnh thang đến chân tường là:
![]() \(h=\sqrt{5^2-x^2}=\sqrt{25-x^2}\) (m)
\(h=\sqrt{5^2-x^2}=\sqrt{25-x^2}\) (m)
b) Với x = 1 thì ![]() \(h= \sqrt{25-1^2} =2\sqrt{6}\) m
\(h= \sqrt{25-1^2} =2\sqrt{6}\) m
Với x = 2 thì ![]() \(h= \sqrt{25-2^2} =\sqrt{21}\) m
\(h= \sqrt{25-2^2} =\sqrt{21}\) m
Với x = 3 thì ![]() \(h= \sqrt{25-3^2} =4\) m
\(h= \sqrt{25-3^2} =4\) m
Với x = 4 thì ![]() \(h= \sqrt{25-4^2} =3\) m
\(h= \sqrt{25-4^2} =3\) m
Thực hành 7 Trang 40 Toán 9 tập 1 Chân trời
Với giá trị nào của x thì biểu thức ![]() \(A=\sqrt{3x+6}\) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai)
\(A=\sqrt{3x+6}\) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai)
Hướng dẫn giải:
Biểu thức A xác định khi 3x + 6 ≥ 0 hay x ≥ − 2.
Ta thấy x = 5 thỏa mãn điều kiện xác định và khi x = 5 ta có
![]() \(A=\sqrt{3.5+6} =\sqrt{21}\)
\(A=\sqrt{3.5+6} =\sqrt{21}\)
Thực hành 8 Trang 40 Toán 9 tập 1 Chân trời
Cho biểu thức ![]() \(P=\sqrt{a^2-b^2}\). Tính giá trị của P khi:
\(P=\sqrt{a^2-b^2}\). Tính giá trị của P khi:
a) a = 5, b = 0
b) a = 5; b = − 5
c) a = 2, b = − 4
Hướng dẫn giải:
a) Với a = 5, b = 0, ta có a2 − b2 = 52 − 02 = 25.
Khi đó, ![]() \(P=\sqrt{25}=5\)
\(P=\sqrt{25}=5\)
b) Với a = 5, b = − 5, ta có a2 − b2 = 52 − (− 5)2 = 0.
Khi đó, P = 0
c) Với a = 2, b = − 4, ta có a2 − b2 = 22 − (− 4)2 = − 12
Vì − 12 < 0 nên biểu thức P không xác định tại a = 2, b = − 4.
Vận dụng 2 Trang 40 Toán 9 tập 1 Chân trời
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)
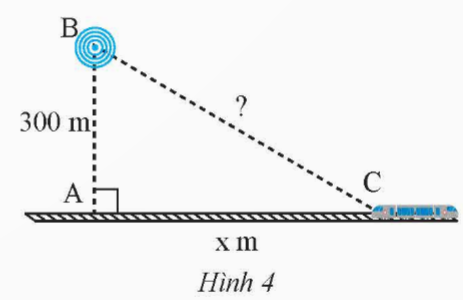
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400, x = 1 000 (kết quả làm tròn đến hàng đơn vị của mét)
Hướng dẫn giải:
a) Áp dụng định lý Pythagore trong tam giác vuông:
Biểu thức biểu thị khoảng cách từ trạm phát sóng đến đầu tàu là:
![]() \(\sqrt{300^2+x^2}\) (m)
\(\sqrt{300^2+x^2}\) (m)
b) Với x = 400, khoảng cách từ trạm phát sóng đến đầu tàu là:
![]() \(\sqrt{300^2+400^2} =500\) (m)
\(\sqrt{300^2+400^2} =500\) (m)
Với x = 1 000, khoảng cách từ trạm phát sóng đến đầu tàu là:
![]() \(\sqrt{300^2+1 000^2} \approx1\ 044\) (m)
\(\sqrt{300^2+1 000^2} \approx1\ 044\) (m)
Giải Toán 9 trang 41
Bài 1 trang 41 Toán 9 Chân trời sáng tạo
Tìm các căn bậc hai của mỗi số sau:
a) 16
b) 2500
c) ![]() \(\frac{4}{{81}}\)
\(\frac{4}{{81}}\)
d) 0,09
Hướng dẫn giải
a) Ta có 42 = 16, nên 16 có hai căn bậc hai là 4 và – 4
b) Ta có 502 = 2500, nên 2500 có hai căn bậc hai là 50 và – 50
c) Ta có ![]() \({\left( {\frac{2}{9}} \right)^2} = \frac{4}{{81}}\) nên
\({\left( {\frac{2}{9}} \right)^2} = \frac{4}{{81}}\) nên![]() \(\frac{4}{{81}}\) có hai căn bậc hai là
\(\frac{4}{{81}}\) có hai căn bậc hai là ![]() \(\frac{2}{9} và – \frac{2}{9}\)
\(\frac{2}{9} và – \frac{2}{9}\)
d) Ta có 0,32 = 0,09 nên 0,09 có hai căn bậc hai là 0,3 và – 0,3.
Bài 2 trang 41 Toán 9 Chân trời sáng tạo
Tính
a) ![]() \(\sqrt {100}\)
\(\sqrt {100}\)
b)![]() \(\sqrt {225}\)
\(\sqrt {225}\)
c) ![]() \(\sqrt {2,25}\)
\(\sqrt {2,25}\)
d) ![]() \(\sqrt {\frac{{16}}{{225}}}\)
\(\sqrt {\frac{{16}}{{225}}}\)
Hướng dẫn giải
a) ![]() \(\sqrt {100} = \sqrt {{{\left( {10} \right)}^2}} = 10\)
\(\sqrt {100} = \sqrt {{{\left( {10} \right)}^2}} = 10\)
b) ![]() \(\sqrt {225} = \sqrt {{{\left( {15} \right)}^2}} = 15\)
\(\sqrt {225} = \sqrt {{{\left( {15} \right)}^2}} = 15\)
c) ![]() \(\sqrt {2,25} = \sqrt {{{\left( {1,5} \right)}^2}} = 1,5\)
\(\sqrt {2,25} = \sqrt {{{\left( {1,5} \right)}^2}} = 1,5\)
d)  \(\sqrt {\frac{{16}}{{225}}} = \sqrt {{{\left( {\frac{4}{{15}}} \right)}^2}} = \frac{4}{{15}}\)
\(\sqrt {\frac{{16}}{{225}}} = \sqrt {{{\left( {\frac{4}{{15}}} \right)}^2}} = \frac{4}{{15}}\)
Bài 3 trang 41 Toán 9 Chân trời sáng tạo
Biết rằng 252 = 625, tìm các căn bậc hai của các số 625 và 0,0625
Hướng dẫn giải
625 có hai căn bậc hai là 25 và – 25
0,0625 có hai căn bậc hai là 0,25 và – 0,25.
Bài 4 trang 41 Toán 9 Chân trời sáng tạo
Sử dụng máy tính cầm tay, tính (kết quả làm tròn đế chữ số thập phân thứ tư):
![]() \(a) \sqrt {54}\)
\(a) \sqrt {54}\)
![]() \(b) \sqrt {24,68}\)
\(b) \sqrt {24,68}\)
![]() \(c) \sqrt 5 + \sqrt 6 + \sqrt 7\)
\(c) \sqrt 5 + \sqrt 6 + \sqrt 7\)
Hướng dẫn giải
![]() \(a) \sqrt {54} \approx 7,3485\)
\(a) \sqrt {54} \approx 7,3485\)
![]() \(b) \sqrt {24,68} \approx 4,9679\)
\(b) \sqrt {24,68} \approx 4,9679\)
![]() \(c) \sqrt 5 + \sqrt 6 + \sqrt 7 \approx 7,3313\)
\(c) \sqrt 5 + \sqrt 6 + \sqrt 7 \approx 7,3313\)
Bài 5 Trang 41 Toán 9 tập 1 Chân trời
Tính giá trị của các biểu thức:
a) ![]() \(\left(\sqrt{5,25}\right)^2+\left(-\sqrt{1,75}\right)^2\)
\(\left(\sqrt{5,25}\right)^2+\left(-\sqrt{1,75}\right)^2\)
b) ![]() \(\left(\sqrt{102}\right)^2-\sqrt{98^2}\)
\(\left(\sqrt{102}\right)^2-\sqrt{98^2}\)
Hướng dẫn giải:
a) ![]() \(\left(\sqrt{5,25}\right)^2+\left(-\sqrt{1,75}\right)^2\)
\(\left(\sqrt{5,25}\right)^2+\left(-\sqrt{1,75}\right)^2\)
= 5,25 + 1,75
= 7
b) ![]() \(\left(\sqrt{102}\right)^2-\sqrt{98^2}\)
\(\left(\sqrt{102}\right)^2-\sqrt{98^2}\)
= 102 − 98
= 4
Bài 6 Trang 41 Toán 9 tập 1 Chân trời
Tìm x, biết:
a) x2 = 121
b) 4x2 = 9
c) x2 = 10
Hướng dẫn giải:
a) x2 = 121
Ta có 112 = 121 nên x = 11 hoặc x = − 11
b) 4x2 = 9 ⇒ ![]() \(x^2=\frac{9}{4}\)
\(x^2=\frac{9}{4}\)
Ta có ![]() \(\left(\frac{3}{2}\right)^2=\frac{9}{4}\) nên
\(\left(\frac{3}{2}\right)^2=\frac{9}{4}\) nên ![]() \(x=\frac{3}{2}\) hoặc
\(x=\frac{3}{2}\) hoặc ![]() \(x=-\frac{3}{2}\)
\(x=-\frac{3}{2}\)
c) x2 = 10
Ta có ![]() \(\left(\sqrt{10}\right)^2=10\) nên
\(\left(\sqrt{10}\right)^2=10\) nên ![]() \(x=\sqrt{10}\) hoặc
\(x=\sqrt{10}\) hoặc ![]() \(x=-\sqrt{10}\)
\(x=-\sqrt{10}\)
Bài 7 Trang 41 Toán 9 tập 1 Chân trời
Tính giá trị của các biểu thức sau khi x = 16, y = 9.
a) ![]() \(\sqrt{x}+\sqrt{y}\)
\(\sqrt{x}+\sqrt{y}\)
b) ![]() \(\sqrt{x+y}\)
\(\sqrt{x+y}\)
c) ![]() \(\frac{1}{2}\sqrt{xy}\)
\(\frac{1}{2}\sqrt{xy}\)
d) ![]() \(\frac{1}{6}x\sqrt{y}\)
\(\frac{1}{6}x\sqrt{y}\)
Hướng dẫn giải:
Với x = 16, y = 9, ta có:
a) ![]() \(\sqrt{x}+\sqrt{y} =\sqrt{16}+\sqrt{9}=4+3=7\)
\(\sqrt{x}+\sqrt{y} =\sqrt{16}+\sqrt{9}=4+3=7\)
b) ![]() \(\sqrt{x+y} =\sqrt{16+9} = \sqrt{25} =5\)
\(\sqrt{x+y} =\sqrt{16+9} = \sqrt{25} =5\)
c) ![]() \(\frac{1}{2}\sqrt{xy} =\frac{1}{2}\sqrt{16.9} =6\)
\(\frac{1}{2}\sqrt{xy} =\frac{1}{2}\sqrt{16.9} =6\)
d) ![]() \(\frac{1}{6}x\sqrt{y} =\frac{1}{6}.16\sqrt{9} =8\)
\(\frac{1}{6}x\sqrt{y} =\frac{1}{6}.16\sqrt{9} =8\)
Bài 9 Trang 41 Toán 9 tập 1 Chân trời
Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?
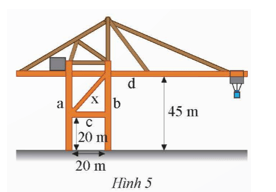
Hướng dẫn giải
Gọi các điểm A, B, C, D, E như trên hình vẽ.
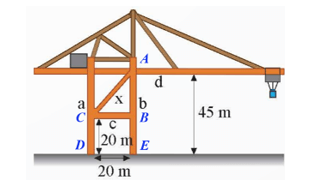
Vì hai trụ a và b đứng cách nhau 20 m nên DE = BC = 20 m.
Vì xà ngang d có độ cao 45 m so với mặt đất nên AE = 45 m.
Suy ra AB = AE – BE = 45 – 20 = 25 (m).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B, ta có:
AC2 = AB2 + BC2 = 252 + 202 = 1025.
Suy ra x = AC = ![]() \(\sqrt{1 025 } ≈ 32\) (m)
\(\sqrt{1 025 } ≈ 32\) (m)
Vậy xà chéo x có độ dài khoảng 32 mét (làm tròn đến hàng đơn vị).









