Giải Toán 9 trang 92 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 92 Tập 1 Chân trời
Giải Toán 9 trang 92 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 92.
Thực hành 2 Trang 92 Toán 9 tập 1 Chân trời
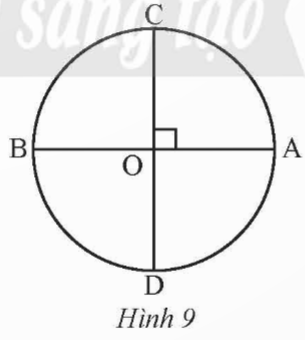
Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung 
\(\overset{\frown}{{AB}} ,\overset{\frown}{{AC}}\) và \(\overset{\frown}{{AD}}\).
Hướng dẫn giải:
Ta có: sđ \(\overset{\frown}{{AB}} = \widehat{AOB} = 180^{\circ}\)
sđ \(\overset{\frown}{{AC}} = \widehat{AOC} = 90^{\circ}\)
sđ \(\overset{\frown}{{AD}} = \widehat{AOD} = 90^{\circ}\)
Vận dụng 2 Trang 92 Toán 9 tập 1 Chân trời
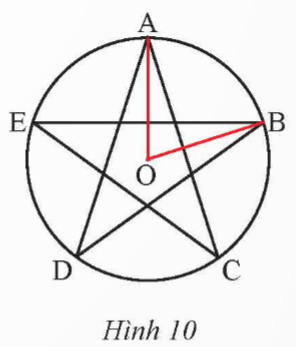
Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10).
Hướng dẫn giải:
Ta có sđ \(\overset{\frown}{{AB}} = \widehat{AOB} = \frac{360^{\circ} }{5} = 72^{\circ}\)
Hoạt động 4 Trang 92 Toán 9 tập 1 Chân trời
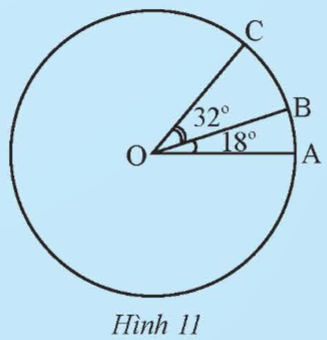
Trên đường tròn (O), vẽ hai cung nhỏ \(\overset{\frown}{{AB}} ,\overset{\frown}{{BC}}\) sao cho \(\widehat{AOB}=18^{\circ} ,\widehat{BOC}=32^{\circ}\) và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung \(\overset{\frown}{{AB}} ,\overset{\frown}{{BC}},\overset{\frown}{{AC}}\).
Hướng dẫn giải:
Do tia OB ở giữa hai tia OA, OC nên
\(\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=18^{\circ} +32^{\circ} =50^{\circ}\)
Vậy sđ \(\overset{\frown}{{AB}} = \widehat{AOB} = 18^{\circ}\)
sđ \(\overset{\frown}{{BC}} = \widehat{BOC} = 32^{\circ}\)
sđ \(\overset{\frown}{{AC}} = \widehat{AOC} = 50^{\circ}\)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 93 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 92 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Góc ở tâm, góc nội tiếp, được VnDoc biên soạn và đăng tải!
