Giải Toán 9 trang 96 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 96 Tập 1 Chân trời
Giải Toán 9 trang 96 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 96.
Thực hành 5 Trang 96 Toán 9 tập 1 Chân trời
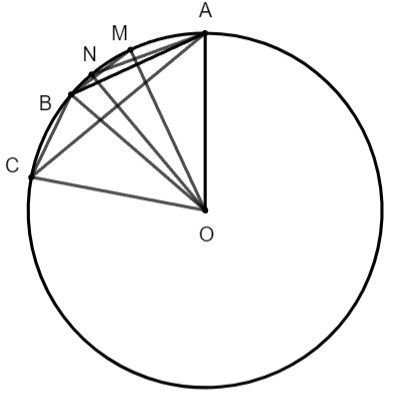
Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho 
\(\widehat{AOB}=50^{\circ} ,\ \widehat{BOC}=30^{\circ}\), điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ \(\overset{\frown}{{AB}},\overset{\frown}{{AC}}\) và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:
a) \(\widehat{BCA},\ \widehat{BAC}\)
b) \(\widehat{MBA},\ \widehat{BAN}\)
Hướng dẫn giải:
a) Ta có: \(\widehat{BCA}=\frac{1}{2} \widehat{AOB} =\frac{1}{2}.50^{\circ} =25^{\circ}\)
\(\widehat{BAC}=\frac{1}{2} \widehat{BOC} =\frac{1}{2}.30^{\circ} =15^{\circ}\)
b) Ta có:
- \(\text{ sđ}\overset{\frown}{{AM}}=\text{ sđ}\overset{\frown}{{MB}} =\frac{1}{2} \text{ sđ}\overset{\frown}{{AB}}\) nên \(\widehat{MBA}=\frac{1}{2} \widehat{MOA} =\frac{1}{2}.25^{\circ} =12,5^{\circ}\)
- \(\text{ sđ}\overset{\frown}{{AC}}=\text{ sđ}\overset{\frown}{{AB}}+\text{ sđ}\overset{\frown}{{BC}}=50^{\circ} +30^{\circ}=80^{\circ}\)
\(\text{ sđ}\overset{\frown}{{AN}}=\text{ sđ}\overset{\frown}{{NC}} =\frac{1}{2} \text{ sđ}\overset{\frown}{{AC}}\) nên \(\widehat{NOC}=\frac{1}{2} \widehat{AOC} =\frac{1}{2}.80^{\circ} =40^{\circ}\)
Vậy \(\widehat{BAN} =\frac{1}{2} \widehat{BON}=\frac{1}{2} \left ( \widehat{NOC}- \widehat{BOC}\right ) =\frac{1}{2} \left ( 40^{\circ} - 30^{\circ} \right ) =5^{\circ}\)
Vận dụng 5 Trang 96 Toán 9 tập 1 Chân trời
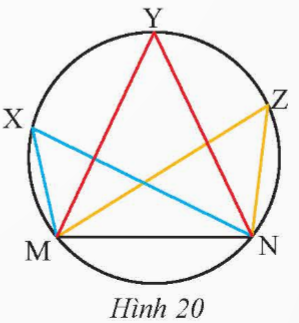
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì \(\widehat{MXN}\) được gọi là góc sút từ vị trí X. Hãy so sánh các góc sút \(\widehat{MXN}, \widehat{MYN},\widehat{MZN}\).
Hướng dẫn giải:
Ta có \(\widehat{MXN}\) là góc nội tiếp chắn cung MN, suy ra \(\widehat{MXN}= \frac12 \text{ sđ}\overset{\frown}{{MN}}\)
\(\widehat{MYN}\) là góc nội tiếp chắn cung MN, suy ra \(\widehat{MYN}= \frac12 \text{ sđ}\overset{\frown}{{MN}}\)
\(\widehat{MZN}\) là góc nội tiếp chắn cung MN, suy ra \(\widehat{MZN}= \frac12 \text{ sđ}\overset{\frown}{{MN}}\)
Vậy \(\widehat{MXN}=\widehat{MYN}=\widehat{MZN}\)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 97 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 96 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Góc ở tâm, góc nội tiếp, được VnDoc biên soạn và đăng tải!
