Giải Toán 9 trang 40 tập 1 Chân trời sáng tạo
Giải Toán 9 trang 40 Tập 1 Chân trời
Giải Toán 9 trang 40 Tập 1 CTST hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 40.
Hoạt động 2 Trang 40 Toán 9 tập 1 Chân trời
Một chiếc thang dài 5 m tựa vào bức tường như Hình 3.
a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1; 2; 3; 4.
Hướng dẫn giải:
a) Áp dụng định lí Pythagore trong tam giác vuông, ta có chiều cao từ đỉnh thang đến chân tường là:
\(h=\sqrt{5^2-x^2}=\sqrt{25-x^2}\) (m)
b) Với x = 1 thì \(h= \sqrt{25-1^2} =2\sqrt{6}\) m
Với x = 2 thì \(h= \sqrt{25-2^2} =\sqrt{21}\) m
Với x = 3 thì \(h= \sqrt{25-3^2} =4\) m
Với x = 4 thì \(h= \sqrt{25-4^2} =3\) m
Thực hành 7 Trang 40 Toán 9 tập 1 Chân trời
Với giá trị nào của x thì biểu thức \(A=\sqrt{3x+6}\) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai)
Hướng dẫn giải:
Biểu thức A xác định khi 3x + 6 ≥ 0 hay x ≥ − 2.
Ta thấy x = 5 thỏa mãn điều kiện xác định và khi x = 5 ta có
\(A=\sqrt{3.5+6} =\sqrt{21}\)
Thực hành 8 Trang 40 Toán 9 tập 1 Chân trời
Cho biểu thức \(P=\sqrt{a^2-b^2}\). Tính giá trị của P khi:
a) a = 5, b = 0
b) a = 5; b = − 5
c) a = 2, b = − 4
Hướng dẫn giải:
a) Với a = 5, b = 0, ta có a2 − b2 = 52 − 02 = 25.
Khi đó, \(P=\sqrt{25}=5\)
b) Với a = 5, b = − 5, ta có a2 − b2 = 52 − (− 5)2 = 0.
Khi đó, P = 0
c) Với a = 2, b = − 4, ta có a2 − b2 = 22 − (− 4)2 = − 12
Vì − 12 < 0 nên biểu thức P không xác định tại a = 2, b = − 4.
Vận dụng 2 Trang 40 Toán 9 tập 1 Chân trời
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)
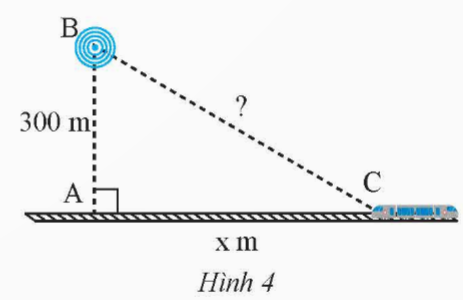
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400, x = 1 000 (kết quả làm tròn đến hàng đơn vị của mét)
Hướng dẫn giải:
a) Áp dụng định lý Pythagore trong tam giác vuông:
Biểu thức biểu thị khoảng cách từ trạm phát sóng đến đầu tàu là:
\(\sqrt{300^2+x^2}\) (m)
b) Với x = 400, khoảng cách từ trạm phát sóng đến đầu tàu là:
\(\sqrt{300^2+400^2} =500\) (m)
Với x = 1 000, khoảng cách từ trạm phát sóng đến đầu tàu là:
\(\sqrt{300^2+1 000^2} \approx1\ 044\) (m)
----------------------------------------------
---> Xem thêm: Giải Toán 9 trang 41 tập 1 Chân trời sáng tạo
Lời giải Toán 9 trang 40 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Căn bậc hai, được VnDoc biên soạn và đăng tải!
